Вдохновившись постом про вычисление pi, решил вычислить подобным образом число e. По пути получилась функция натурального логарифма.

Собственно,
#include <iostream>
#define I r=
#define l ;
#define o
#define x if(1+(d*2)*(1/(__*2))<=k)d++;
#define e p+=d;d=1;
#define h _++;
#define s __++;
double ln(double k){double p=0,n,y,r,d, _=0,__=0;
I 3.30 l o o o o o o
I 3.25 l o o o o o o
I 3.20 l o o o o o o
I 3.15 l o o o o o o
I 3.10 l o o o o o o
I 3.05 l o o o o o o
I 3.00 l o o o o o o
I 2.95 l o o o o o o
I 2.90 l o o o o o o
I 2.85 l o o o o o o
I 2.80 l o o o o o o
I 2.75 l o o o o o o o
I 2.70 l o o o o o o o
I 2.65 l o o o o o o o
I 2.60 l o o o o o o o
I 2.55 l o o o o o o o
I 2.50 l o o o o o o o
I 2.45 l o o o o o o o
I 2.40 l o o o o o o o o
I 2.35 l o o o o o o o o
I 2.30 l o o o o o o o o
I 2.25 l o o o o o o o o
I 2.20 l o o o o o o o o
I 2.15 l o o o o o o o o
I 2.10 l o o o o o o o o
I 2.05 l o o o o o o o o
I 2.00 l o o o o o o o o
I 1.95 l o o o o o o o o o
I 1.90 l o o o o o o o o o
I 1.85 l o o o o o o o o o
I 1.80 l o o o o o o o o o
I 1.75 l o o o o o o o o o
I 1.70 l o o o o o o o o o
I 1.65 l o o o o o o o o o
I 1.60 l o o o o o o o o o
I 1.55 l o o o o o o o o o o
I 1.50 l o o o o o o o o o o
I 1.45 l o o o o o o o o o o
I 1.40 l o o o o o o o o o o
I 1.35 l o o o o o o o o o o o
I 1.30 l o o o o o o o o o o o
I 1.25 l o o o o o o o o o o o
I 1.20 l o o o o o o o o o o o o
I 1.15 l o o o o o o o o o o o o
I 1.10 l o o o o o o o o o o o o
I 1.05 l o o s s s s s s s s s s o
I 1.00 l o o h h h h h h h h h h o
I 0.95 l o o h h h h h h h h h h e o
I 0.90 l o o h h h h h h h h h h e o
I 0.85 l o o h h h h h h h h h h e x o
I 0.80 l o o h h h h h h h h h h e x x o
I 0.75 l o o h h h h h h h h h h e x x x o
I 0.70 l o o h h h h h h h h h h e x x x x o
I 0.65 l o o h h h h h h h h h h e x x x x x o
I 0.60 l o o h h h h h h h h h h e x x x x x x o
I 0.55 l o o h h h h h h h h h h e x x x x x x x x o
I 0.50 l o o h h h h h h h h h h e x x x x x x x x x x o
I 0.45 l o o h h h h h h h h h h e x x x x x x x x x x x x x x o
I 0.40 l o o h h h h h h h h h h e x x x x x x x x x x x x x x x x x o
I 0.35 l o o h h h h h h h h h h e x x x x x x x x x x x x x x x x x x x x x x o
I 0.30 l o o h h h h h h h h h h e x x x x x x x x x x x x x x x x x x x x x x x x x x x o
I 0.25 l o o h h h h h h h h h h e x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x
I 0.20 l o o h h h h h h h h h h e x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x
I 0.15 l o o h h h h h h h h h h e x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x
I 0.10 l o o h h h h h h h h h h e x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x x e return p/_;
// 0 +1 +2 +3 +4 +5
}
Принцип прост — натуральный логарифм от a есть площадь под графиком 1/x от единицы до a.
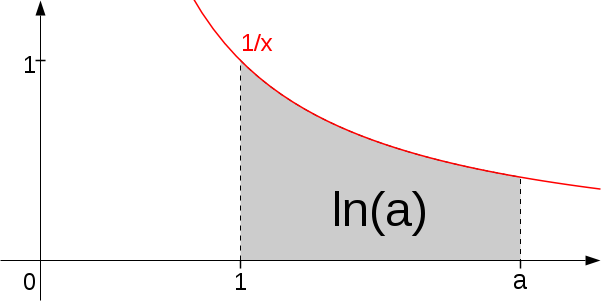
Соответственно, чем точнее нарисован график, тем точнее будут вычисления. Немного о построении графика. Символами s обозначается единичный отрезок, h — квадрат единичной площади, e — функция x=1, x — площадь под графиком 1/x на отрезке (1, +inf).
Имея функцию натурального логарифма и зная, что ln(e)=1 найти теперь e перебором не составляет труда.
for(double i = 0; i <= 3; i += 0.01)
{
if (ln(i) > 0.98)
{
std::cout << i << std::endl;
break;
}
Некоторые результаты:
| Выражение | Значение | Истинное значение |
| ln(2) | 0.721053 | 0.69315 |
| ln(2.7) | 1 | 0.99325 |
| ln(3) | 1.09474 | 1.09861 |
| ln(4) | 1.35263 | 1.38629 |
| ln(5) | 1.54211 | 1.60943 |
| e | 2.7 | 2.718281828 |
Ссылка на полный код.
Автор: devpony






