Статьи по небесной механике пользуются на Хабре некоторой популярностью, поэтому я решил рассказать
об одном фундаментальном уравнении движения, а именно, уравнении Кеплера.
Как известно, финитное движение небесных тел в Солнечной системе происходит по эллипсу. Однако, если необходимо
установить, в какой точке небесное тело находится в заданный момент времени,
этой информации недостаточно и надо воспользоваться уравнением Кеплера.
Выведем это уравнение.
Напомню, что эллипс — это сплюснутая на величину
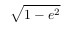
окружность. Здесь e — эксцентриситет.
Площадь эллипса равна
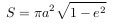
a — большая полуось.
Согласно второму закону Кеплера, который гласит, что площадь,
заметаемая радиус-вектором небесного тела пропорциональна времени,
можно написать
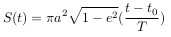
где T — период обращения, t — текущее время,
t0 — момент времени прохождения перигелия (ближайшей к Солнцу точки орбиты).
Найдем теперь зависимость этой площади от положения небесного тела на орбите,
то есть от величины радиус-вектора r и истинной аномалии — угла между перигелием и небесным телом,
если смотреть с Солнца.
Для этого введем дополнительную переменную — эксцентрическую аномалию E.
Направим ось x от Солнца (начала координат), которое находится в одном из фокусов эллипса, в сторону перигелия
по линии апсид (прямой, соединяющей перицентр с апоцентром).
Создадим также вспомогательную окружность с радиусом, равным большой полуоси эллипса.
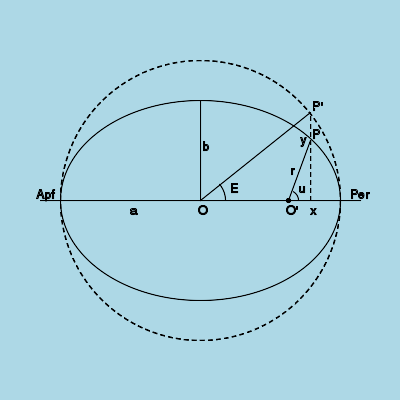
Абсцисса небесного тела в точке P
будет равна
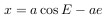
ордината будет, соответственно, равна
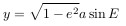
Таким образом, получаем
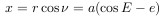
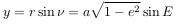
Для вычисления площади S рассмотрим две вспомогательные фигуры:
сектор окружности P'-O-Per:
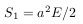
Сектор эллипса P-O-Per:
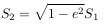
Треугольник O-O'-P:
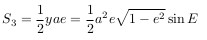
Сектор P-O'-Per:
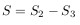
Отсюда, прощадь S равна:
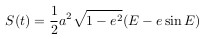
Сравнивая это выражение с выведенным ранее из второго закона Кеплера,
получаем:
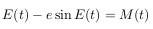
Это и есть уравнение Кеплера.
Заметим, что это трансцендентное уравнение относительно E и получить явное решение
в общем случае не удается.
Для вычисления координат небесного тела необходимо найти эксцентрическую аномалию по известному M и e, a затем определить радиус-вектор и угол и, если необходимо x и y по приведенным выше формулам.
Интересным вопросом остается нахождение методов решения уравнения Кеплера.
Этим занимались лучшие умы человечества на протяжении последних четырехсот лет.
Результатом было обогащение математики множеством интересных идей, но описание этого
требует отдельной статьи.
Автор: andy_p



