Производящие функции — туда и обратно

«Производящая функция является устройством, отчасти напоминающим мешок. Вместо того чтобы нести отдельно много предметов, что могло бы оказаться затруднительным, мы собираем их вместе, и тогда нам нужно нести лишь один предмет — мешок».
                                                                                                                                                               Д. Пойа

Введение

Математика делится на два мира — дискретный и непрерывный. В реальном мире есть место и для того и для другого, и часто к изучению одного явления можно подойти с разных сторон. В этой статье мы рассмотрим метод решения задач с помощью производящих функций — мостика ведущего из дискретного мира в непрерывный, и наоборот.

Идея производящих функций достаточно проста: сопоставим некоторой последовательности <g₀, g₁, g₂, ..., g_n> — дискретному объекту, степенной ряд g₀ + g₁z + g₂z² +… + g_nzⁿ +… — объект непрерывный, тем самым мы подключаем к решению задачи целый арсенал средств математического анализа, который как мы все знаем очень большой.

Вышесказанное можно записать с помощью математических формул следующим образом: <g₀, g₁, g₂, ..., g_n> <=> g₀ + g₁z + g₂z² +… + g_nzⁿ +…. Обычно говорят, последовательность генерируется, порождается производящей функцией. Важно понимать, что это символьная конструкция, то есть вместо символа z может быть любой объект, для которого определены операции сложения и умножения.

История возникновения производящих функций

Известно, что начало производящим функциям положил английский математик Абрахам де Муавр, а дальнейшему развитию и продолжению данного метода мы обязаны великому математику, имя которого Леонард Эйлер.

В 50-х годах XVIII века Эйлер решал следующую задачу: какие грузы можно взвесить с помощью гирь в 2⁰, 2¹, 2²,..., 2ⁿ грамм и сколькими способами? При решении этой задачи он использовал никому неизвестный на то время метод производящих функций, которому и посвящена данная статья. К этой задаче мы вернемся немного позже, после того как разберемся более подробно с устройством производящих функций.

Метод производящих функций

Изучение этого мощного механизма позволяющего решать многие комбинаторные задачи и не только, мы начнем с простенькой задачи: сколькими способами можно расположить в линию черные и белые шары, общее количество которых равно n?

Обозначим белый шар символом ○, черный — ●, T_n — искомое количество расположений шаров, общее количество которых равно n. Символом Ø обозначим нулевое количество шаров. Как и любое решение комбинаторной задачи начнем с тривиальных случаев:

Если n = 1, то очевидно имеется 2 способа — взять либо белый шар ○, либо взять черный шар ●, таким образом, T₂ = 2.

Если n = 2, то имеется 4 способа расположений: ○○, ○●, ●○, ●●.

Рассмотрим случай для n = 3. Мы можем начать белым шаром и продолжить 4-мя комбинациями, описанными выше ○○○, ○○●, ○●○, ○●●, или же мы можем начать черным шаром и аналогично продолжить 4-мя способами ●○○, ●○●, ●●○, ●●●.

В итоге количество шаров удвоилось, то есть T₃ = 2T₂. Аналогично T₄ = 2T₃, то есть, обобщая для всех n получаем рекуррентное уравнение T_n = 2T_n-1 которое и является решением для данной задачи. Решение такого уравнения можно легко угадать — T_n = 2ⁿ (так как 2⋅2^n-1 = 2ⁿ).

А что если у нас плохо с угадыванием? И что делать, если уравнение будет сложнее? А вообще причем здесь производящие функции?

«Просуммируем» все возможные комбинации расположений шаров:

G = Ø + ○ + ● + ○○ + ○● + ●○ + ●● + ○○○ + ○○● + ○●○ + ○●● + ●○○ + ●○● + ●●○ + ●●● +…

Вопрос о справедливости такой нелепой на первый взгляд суммы опустим. Будем складывать и умножать последовательности шаров. Со сложением все понятно, но что значит умножение шаров? Перемножив ○● на ●○ мы получим не что иное как ○●●○. Заметим, однако, что произведение шаров в отличие от произведения чисел не является коммутативным, то есть ○●⋅●○ ≠ ●○⋅○●. Символ Ø — в произведении играет роль мультипликативной единицы, то есть Ø ⋅ ○○● = ○○● ⋅ Ø = ○○●.

Произведем с рядом G последовательность манипуляций, а именно вынесем за скобки белый и черный шары:

G = Ø + ○ (Ø + ○ + ● + ○○ + ○● + ●○ + ●● + ...) + ● (Ø + ○ + ● + ○○ + ○● + ●○ + ●● + ...) = Ø + ○G +●G.

Решая, это уравнение относительно G находим: .
Вспоминая формулу суммы геометрической прогрессии: , имеем .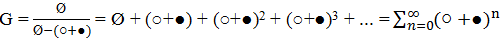

В этой сумме так же учтены все возможные варианты разбиения в точности по одному разу, просто в другом порядке.

Далее воспользуемся формулой бинома Ньютона: 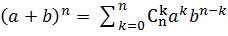, где 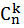— число сочетаний из n по k.

Тогда с учетом этого имеем: .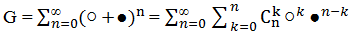

Коэффициент при ○^k ●^n-k равен 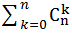показывает общее количество последовательностей из n шаров содержащих ○ шары в количеств k штук и ● шары в количестве n-k штук. Как известно .

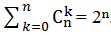Эту формулу можно было получить непосредственно из 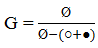заменив Ø на 1, а ○ и ● на z (так как цвет шара не играет роли). Получим 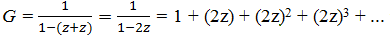, то есть коэффициент при zⁿ равен 2ⁿ.

Обсуждение метода

Так что же позволяет данному методу быть работоспособным при решении различных задач?

Алгоритм решения задачи можно описать примерно следующим образом: рассматривается некоторая бесконечная сумма, которая в конечном итоге представляет собой формальный степенной ряд G(z) = g₀ + g₁z + g₂z² +… + g_nzⁿ +… причем коэффициенты g_k — являются ключом к решению исходной задачи. Тот факт, что ряд является формальным, говорит о том, что z — является просто символом, вместо него может быть любой объект: число, шар, кость домино и т.д. В отличие от степенных рядов в анализе формальным степенным рядам не придается числовых значений и, соответственно, нет смысла говорить о сходимости таких рядов для числовых аргументов.

G(z) = g₀ + g₁z + g₂z² +… + g_nzⁿ +… — называется производящей функцией для последовательности чисел <g₀, g₁, g₂, ..., g_n>. Заметим, однако, что хотя G(z) — функция, это всё таки формальная запись, то есть мы не можем подставить вместо z значение z = z₀, за исключением z = 0, так как G(0) = g₀.

Затем производя различные преобразования с бесконечной суммой G(z) мы преобразуем её к замкнутому (компактному) виду. То есть у производящей функции есть 2 представления: бесконечное и замкнутое и, как правило, для решения задачи необходимо бесконечный вид преобразовать к замкнутому.

После этого преобразования нам необходимо этот компактный вид разложить в степенной ряд и получить значения для коэффициентов g_k.

Отвечая на поставленный вначале вопрос можно сказать так: успех данного метода связан с возможностью записать производящую функцию в замкнутом виде. Так, например, производящая функция для последовательности <1, 1, 1, ..., 1> в бесконечном виде представляется как 1 + x + x² + x³ + ..., а в замкнутом .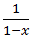

А теперь вооружившись знаниями, вернемся к задаче, которую решал Эйлер.

Итак, задача звучит следующим образом: какие грузы можно взвесить с помощью гирь в 2⁰, 2¹, 2²,..., 2ⁿ грамм и сколькими способами?

Я не знаю, как долго Эйлер придумывал решение для этой задачи, но оно поражает своей неожиданностью. Посудите сами. Эйлер рассматривает произведение G(z) = (1+z)(1+z²)(1+z⁴)(1+z⁸)… которое после раскрытия скобок представляется в виде бесконечного ряда G(z) = g₀ + g₁z + g₂z² +… + g_nzⁿ +….

Что же из себя представляют коэффициенты g_k? Каждый g_k — это коэффициент при z^k, а z^k — получается как произведение каких-то одночленов z^2m, то есть g_k — это в точности число разных представлений числа k в виде суммы некоторых из чисел 2⁰, 2¹, 2², 2³,...,2^m,…. Другими словами g_k — это число способов взвешивания груза в k грамм заданными гирями. Как раз то, что мы искали!

Следующий шаг Эйлера не менее удивителен. Он умножает обе части равенства на (1-z).

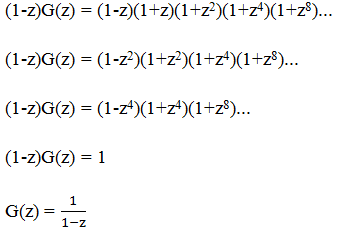
С одной стороны G(z) = g₀ + g₁z + g₂z² +… + g_nzⁿ +… с другой стороны мы только что получили G(z) = 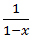. Но ведь 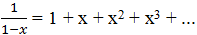. Сопоставляя эти два равенства, получаем g₁ = g₂ = g₃ =… = 1, то есть любой груз в k грамм можно взвесить гирями в 1, 2, 4, 8,… грамм притом единственным способом.

Вот так вот Эйлер применил метод производящих функций при решении задач.

Решение рекуррентных соотношений

Производящие функции показывают себя с хорошей стороны не только при решении комбинаторных задач. Оказывается, они идеально подходят для решения рекуррентных соотношений.

Начнем со всеми знакомой последовательностью чисел Фибоначчи. Каждый из нас знает ее рекуррентный вид: F₀ = 0, F₁ = 1, F_n = F_n-1 + F_n-2 ,n ≥ 2. Однако не каждый знает вид этой формулы в замкнутом виде и это не удивительно, ведь она содержит иррациональное число в своем составе (кстати, это число есть не что иное как «золотое сечение»).

Итак, имеем

F₀ = 0,
F₁ = 1,
F_n = F_n-1 + F_n-2, n ≥ 2

Умножим каждую строчку на z⁰, z¹, ..., zⁿ соответственно:

z⁰ ⋅ F₀ = 0,
z¹ ⋅ F₁ = z,
zⁿ ⋅ F_n = zⁿ ⋅ F_n-1 + zⁿ ⋅ F_n-2 ,n ≥ 2

Просуммируем эти равенства:

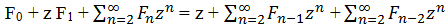
Обозначим левую часть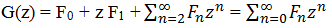

Рассмотрим каждое из слагаемых в правой части:

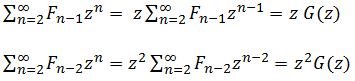
Имеем следующее уравнение:

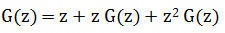
решая которое относительно G(z) находим 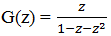— производящая функция для последовательности чисел Фибоначчи. Следующим шагом является ее разложение в степенной ряд, а для этого разложим ее на сумму простейших дробей.
Корни уравнения 1 — z — z² = 0 —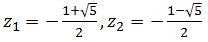
Тогда нашу производящую функцию можно разложить следующим образом:

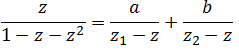
Методом неопределенных коэффициентов или подстановки различных значений z находим .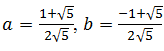
Напоследок немного преобразуем выражение для производящей функции:

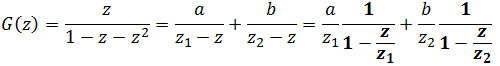
Теперь каждая из дробей представляет собой сумму геометрической прогрессии. По формуле

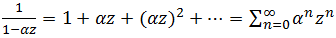находим .

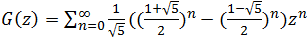Но ведь мы искали G(z) в виде 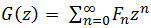. Отсюда делаем вывод, что

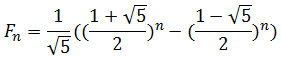
Эту формулу можно переписать в другом виде не используя «золотое сечение»:

,
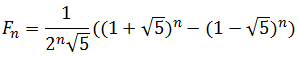что достаточно трудно было ожидать, учитывая красивое рекуррентное уравнение.

Давайте запишем общий алгоритм решения рекуррентных уравнений, используя производящие функции. Он записывается в 4 шага:

1. Запишите одно уравнение, выражающее g_n через другие элементы последовательности. Это уравнение должно оставаться справедливым для всех целых n с учетом того, что g_-1=g_-2=....=0.
2. Умножьте обе части уравнения на zⁿ и просуммируйте по всем n. В левой части получится сумма 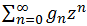, которая равна производящей функции G(z). Правую часть следует преобразовать так, чтобы она превратилась в какое-то другое выражение, включающее G(z).
3. Решите полученное уравнение, получив для G(z) выражение в замкнутом виде.
4. Разложите G(z) в степенной ряд и прочитайте коэффициент при zⁿ, это и будет замкнутый вид для g_n.

Причина работоспособности этого метода в том, что единая функция G(z) представляет всю последовательность g_n и это представление допускает многие преобразования.

Давайте для закрепления алгоритма рассмотрим еще один пример (более сложный). Пусть надо решить такое рекуррентное уравнение:

g₀ = 1,
g₁ = 1,
g_n = g_n-1 + 2g_n-2 + (-1)ⁿ

По первым значениям n трудно сказать что-либо об общей формуле:

n	0	1	2	3	4	5	6
gn	1	1	4	5	14	23	52

Будем следовать вышеописанному алгоритму. Первое условие алгоритма выполнено. Умножим обе части всех равенств на z в соответствующей степени и просуммируем:

z⁰⋅g₀ = 1,
z⋅g₁ = z,
zⁿ⋅g_n = zⁿ⋅g_n-1 + 2zⁿ⋅g_n-2 + (-1)ⁿ⋅zⁿ

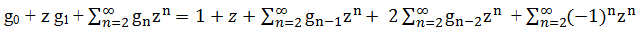
Левая часть 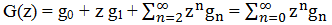— представляет собой производящую функцию в бесконечном виде.

Попытаемся выразить правую часть через G(z). Рассмотрим каждое слагаемое:

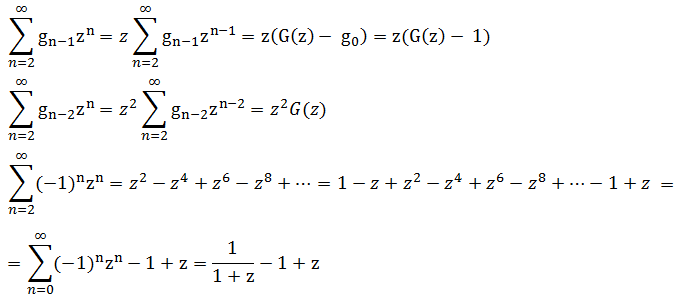
Составляем уравнение:

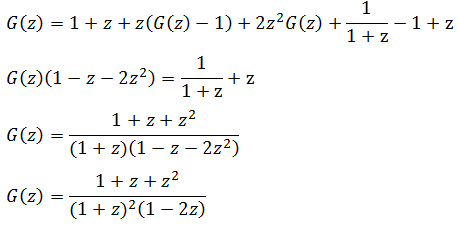
Это и есть производящая функция для заданного рекуррентного уравнения в замкнутом виде. Раскладывая её на простейшие дроби (например, методом неопределенных коэффициентов или методом подстановки различных значений z), получаем:

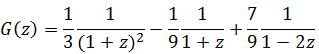
Второе и третье слагаемые легко раскладываются в степенной ряд, а вот с первым придется чуть повозиться:

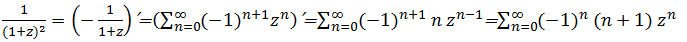
Собственно все. Раскладываем каждое слагаемое в степенной ряд и получаем ответ:

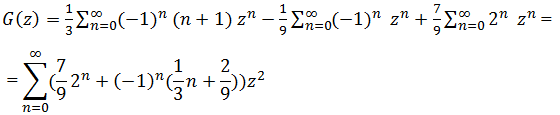
С одной стороны мы искали G(z) в виде 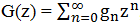, с другой стороны .

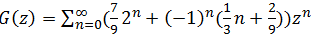Значит, .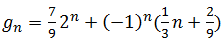

Попробуйте решить такое рекуррентное уравнение:

g₀ = 1,
g₁ = 2,
g_n = 6g_n-1 — 8g_n-2 + n

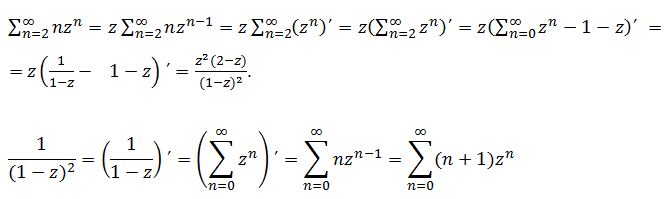
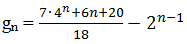
Заключение

Как вы поняли, производящие функции являются достаточно серьезным механизмом решения многих задач (комбинаторных и не только). К числу таковых я могу отнести: задача об укладывании паркета, задача о счастливых билетах, задача о взвешивании, задача о разбиении числа, задача о размене, и это только то, что знаю я. Так же производящие функции позволяют решать рекуррентные уравнения, причем алгоритм решения не зависит от вида самого уравнения, этим они и отличаются от других способов, которые в свою очередь являются индивидуальными для каждого уравнения.

На этой веселой ноте, пожалуй, мы и закончим знакомство с производящими функциями, надеюсь, оно было увлекательным и познавательным.

Автор: timyrik20

Источник