1. Об аттракторе Лоренца
Эдвард Нортон Лоренц (1917 – 2008) является основателем теории хаоса, очень популярной в науке на сегодняшний день. Он учился в колледже Дартмут штата Нью-Гемпшир США и Гарвардском университете в Кембридже. Во время Второй мировой войны служил метеорологом в авиационном корпусе армии США, потом до конца своих дней работал профессором в Массачусетском технологическом институте.
В 1963 году в журнале «Journal of the Atmospheric Sciences» вышла его статья «Deterministic Nonperiodic Flow» (русский перевод: Лоренц Э. Детерминированное непериодическое течение // Странные аттракторы. — М.: Мир, 1981, с. 88-117), заложившая не только основы теории хаоса, но и изменившая представления о моделировании погодных явлений. В этой работе из системы уравнений Навье-Стокса впервые была получена нелинейная автономная система обыкновенных дифференциальных уравнений третьего порядка (динамическая система), описывающая движение воздушных потоков в плоском слое жидкости постоянной толщины при разложении скорости течения и температуры в двойные ряды Фурье с последующем усечением до первых-вторых гармоник:
(1) 
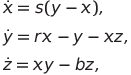
где s, r и b — некоторые положительные числа, параметры системы. Обычно исследования системы Лоренца проводят при s = 10, r = 28 и b = 8/3 (классические значения параметров).
Вообще, теория хаоса — раздел математики, изучающий поведение детерминированных динамических систем, где решения имеют достаточно сложную структуру, поэтому кажется, что во времени они ведут себя случайным образом. Детерминированная система — система, уравнения движения, параметры и начальные условия которой известны и не являются случайными (Мун Ф. Хаотические колебания. — М.: Мир, 1990).
Динамическая система (1) также возникает и в других процессах:
1. Конвекция в тороидальной трубе (Ланда П.С. Нелинейные колебания и волны. — М: ЛИБРОКОМ, 2010, с. 454-455);
2. Одномодовый лазер (Покровский Л.А. Решение системы уравнений Лоренца в асимптотическом пределе большого числа Релея. I. Система Лоренца в простейшей квантовой модели лазера и приложение к ней метода усреднения // Теоретическая и математическая физика, 1985, т. 62, №2, с. 272-290);
3. Осциллятор с инерционным возбуждением (Неймарк Ю.И., Ланда П.С. Стохастические и хаотические колебания. — М: ЛИБРОКОМ, 2009, с. 288-295).
Для любого решения системы Лоренца существует такой момент времени, когда соответствующая фазовая траектория навсегда погружается в сферу фиксированного радиуса. Поэтому существует предельное множество — аттрактор Лоренца, — к которому притягиваются все траектории динамической системы при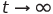 
(Немыцкий В.В., Степанов В.В. Качественная теория дифференциальных уравнений. — М.: Едиториал УРСС, 2004, с. 357-359). Таким образом, аттрактор определяет поведение решений системы (1) на больших отрезках времени.
Из-за отсутствия точных методов решения нелинейных динамических систем общего вида для анализа структуры аттрактора часто применяют численные методы такие, как, например, сочетание явной схемы Эйлера с центрально-разностной схемой, Адамса, использование старших производных, а также Рунге-Кутта 4-ого порядка. В случае классических значений параметров системы наблюдается неустойчивость ее решений, поскольку положения равновесия системы имеют седловой тип. Это ограничивает применение указанных методов, поскольку растет общая ошибка с увеличением отрезка интегрирования. Таким образом, небольшие изменения в начальных условиях системы (1) (т.е. атмосферы) могут привести со временем к значительным последствиям.
В 70-х гг. 20-ого века Гукенхеймер, Уильямс и Йорке на основе результатов численных экспериментов сформулировали гипотезу о структуре аттрактора Лоренца при классических значениях параметров системы, однако, соответствие этой гипотезы структуре притягивающего множества системы (1) строго не доказано. В 2000 году Стивен Смейл составил список из 18 наиболее значительных математических проблем 21-ого века. Проблема структуры аттрактора Лоренца была включена в этот перечень под номером 14. Считается, что она была решена Уориком Такером в 2002 году при помощи дискретной алгебры, но многие математики так и не приняли его доказательства хотя бы потому, что строго не показано наличие периодических решений в системе (1).
В литературе, посвященной численному исследованию системы Лоренца при классических значениях ее параметров, очень часто делаются заключения о структуре аттрактора на основе данных, полученных из вычислительного эксперимента (например, что аттрактор содержит циклы). При этом нет достаточных обоснований о выборе шага, с какими типами вещественных чисел приходилось работать, и на каком отрезке времени производились расчеты.
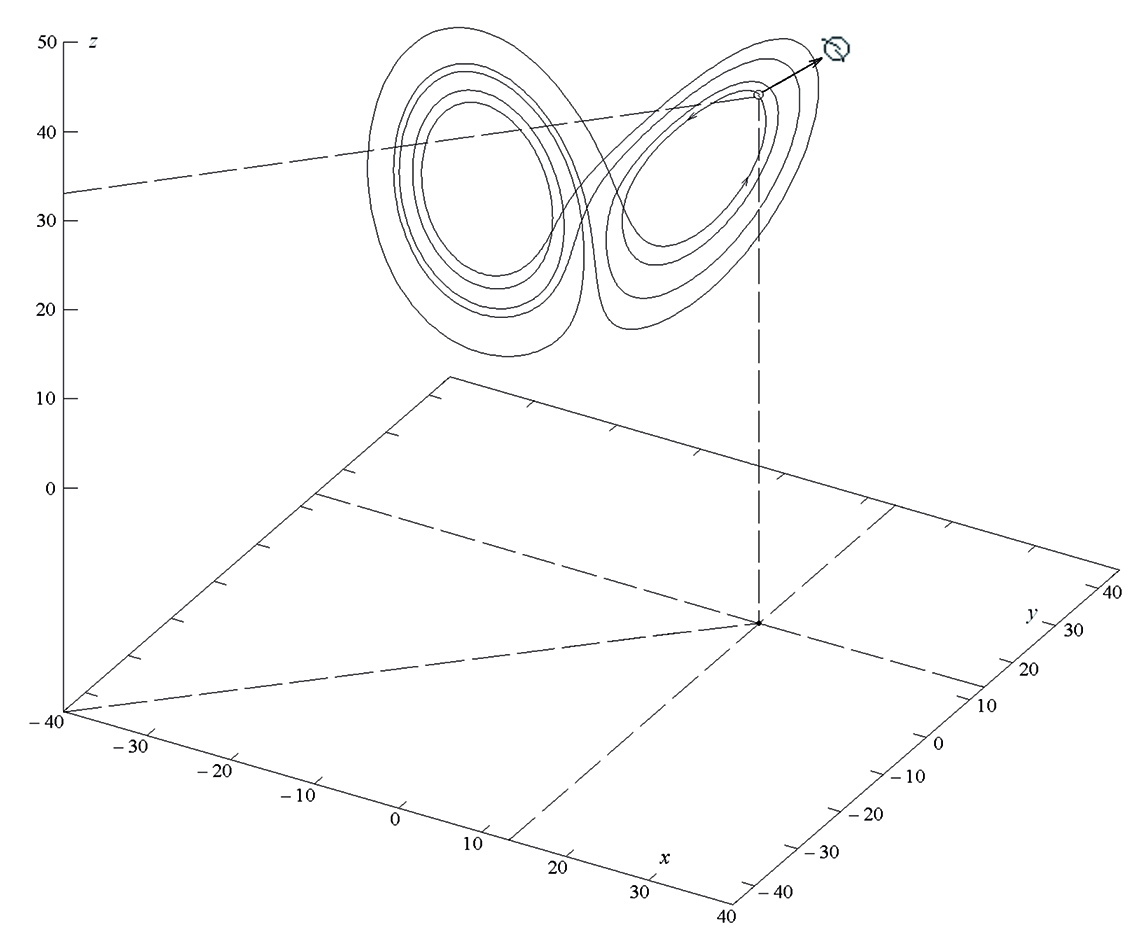
Рис. 1. Дуга траектории, построенная на отрезке времени [0;6.827] для x(0)=13.41265629, y(0)=13.46430003, z(0)=33.46156416.
По теореме Биркгофа (Немыцкий В.В., Степанов В.В. Качественная теория дифференциальных уравнений. — М.: Едиториал УРСС, 2004, с. 402) аттрактор Лоренца содержит рекуррентные траектории, а каждое рекуррентное движение устойчиво по Пуассону. Это означает, что найдутся сколь угодно большие значения моментов времени, что точка на траектории системы оказывается в любой окрестности своего начального положения. Таким рекуррентным движением может быть и цикл, но делать вывод об этом, исходя из найденного возврата траектории в некоторую окрестность начальных условий, нельзя. Как показали расчеты (рис. 1), в системе Лоренца динамика поведения решений на аттракторе достаточно сложна, и рекуррентные траектории, содержащиеся в нем, могут, например, описываться почти периодическими решениями или иметь более сложную структуру. Мной был построен пример неавтономной системы с таким поведением решений.
2. Моделирование динамики системы Лоренца
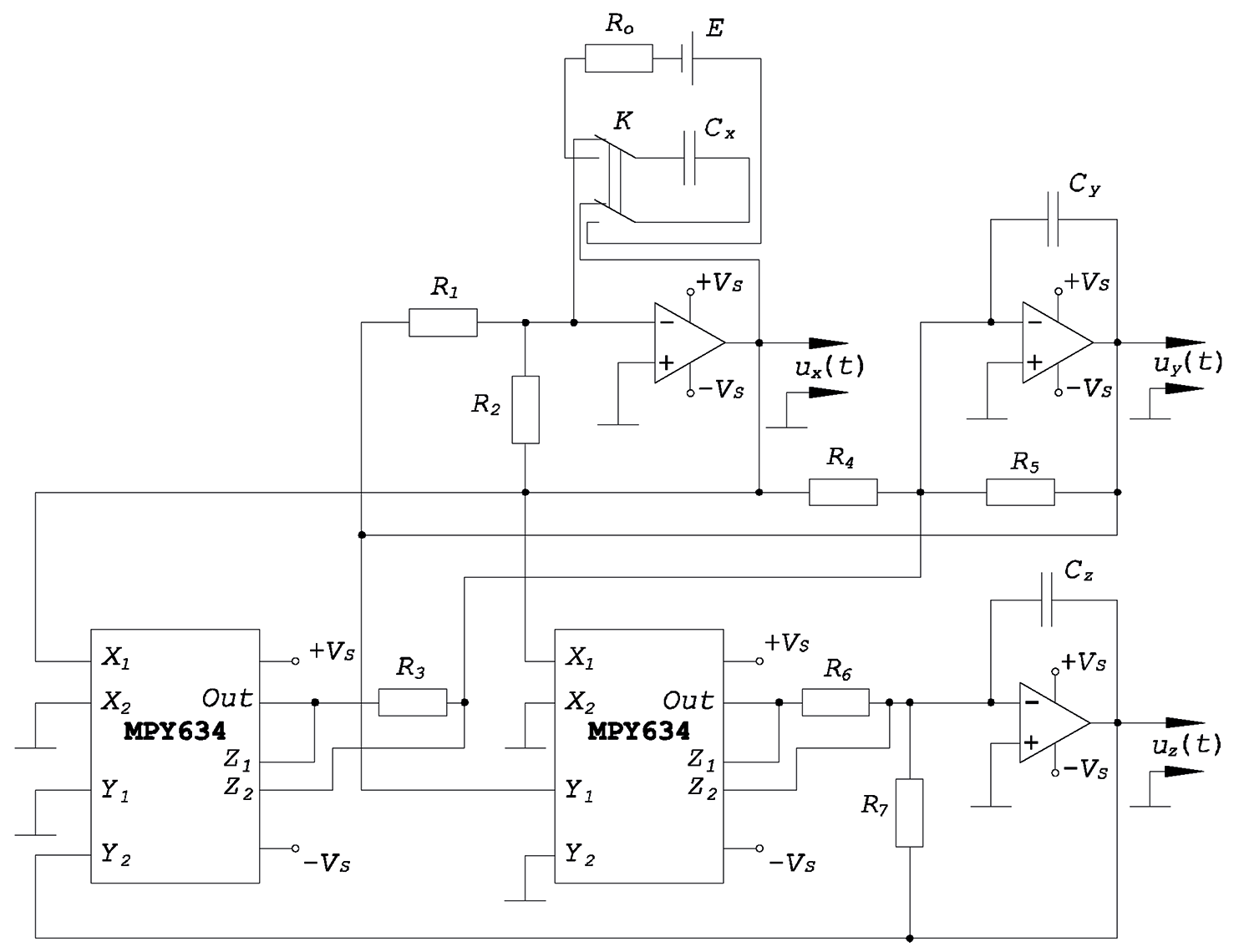
Рис. 2. Схема генератора колебаний, описывающих динамику системы Лоренца.
Для генерации сигналов (хаотических колебаний), описывающих траектории на аттракторах динамических систем с определенными видами нелинейностей правых частей, на практике также применяют физическое моделирование с помощью электрических схем /или аналоговых вычислительных машин/ (Дмитриев А.С., Панас А.И. Динамический хаос: новые носители информации для систем связи. — М.: Физматлит, 2002).
Рассмотрим электрическую схему генератора колебаний, представленную на рис. 2, как альтернативу численному моделированию. Поскольку система Лоренца имеет третий порядок, то для создания динамики изменения напряжений в цепи необходимы три интегратора на базе операционных усилителей, поскольку с дифференциаторами связаны проблемы шума. При этом для построения схемы и записи интегральных уравнений использовалась базовая схема включения современного аналогового умножителя MPY634, приведенная на рис. 3 в официальной документации производителя микросхемы. Имеем:
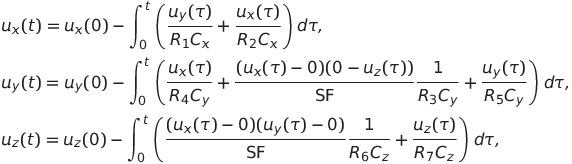
где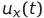 
, 
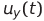и 
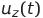— мгновенные значения напряжений, соответствующие функциям x(t), y(t) и z(t) (пара из этих напряжений может быть подана на пластины осциллографа — полученная сложная фигура является проекцией траектории системы Лоренца на соответствующую плоскость), 
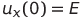и 
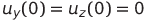— начальные напряжения на конденсаторах 
, 
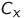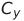и 
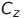соответственно, SF = 10 В — масштабный коэффициент умножителя.
Первоначально производится зарядка конденсатора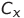 
от источника питания E; резистор 
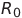предусмотрен для перезарядки (состояние ключа K показано на рисунке в цепи генератора). Остальные конденсаторы имеют нулевой начальный заряд. По сути мы задаем начальные условия для системы (1). Схему начальной зарядки можно изменить (например, заряжать два конденсатора), за исключением ситуации, когда 
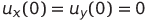. Это объясняется тем, что 
, 
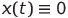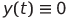и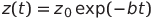 
— частное решение системы (1), где 
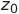— произвольная постоянная. Понятно, что в этом случае никаких колебаний не будет.
Сделаем замену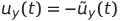 
и продифференцируем по времени обе части каждого интегрального уравнения. Получим
(2) 
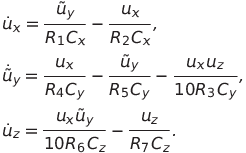
Будем моделировать динамику при классических значениях параметров системы (1). Положим величины сопротивлений и емкостей равными
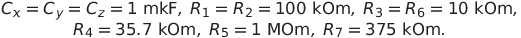
Тогда система (2) примет вид
(3) 
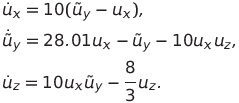
Делая в (3) замену
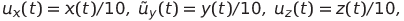
получим систему Лоренца. Поскольку
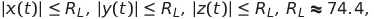
то из введенной замены следует, абсолютная величина напряжения не превысит величины 7.44 В, что предусматривается документацией умножителя MPY634. Значение E можно выбрать равным 1.5 В (ЭДС пальчиковой батарейки).
Точность представленной модели определяется погрешностями реальных емкостей и сопротивлений, а также частотными характеристиками интеграторов и умножителей.
P.S.
Недавно мной был сделан доклад по данной теме на математической конференции. Посмотреть его можно здесь (заранее прошу прощения за качество видео). Там же можно загрузить и материалы доклада (лучше просматривать презентацию синхронно с докладом, поскольку из-за качества видео ее нечетко видно).
Автор: pchelintsev_an
