Встала задача перебрать все возможные варианты «триангуляций». Это «склейки» из N треугольников, которые подчиняются простым правилам:
- Соприкасаться треугольники могут только по ребру
- Одно ребро может быть общим только у двух треугольников, не больше
Например, из трёх треугольников уникальных вариантов может быть всего два:
[[A B C], [A B D], [A C D]]
[[A B C], [A B D], [A C E]]
При том, что всего вариантов склеек 120. Мне удалось неплохо оптимизировать процесс перебора, который позволил просчитать почти все варианты вплоть до N = 11, но это всё равно очень мало.
Я расскажу как оптимизировал, может быть у уважаемой публики появятся идеи как этот процесс еще ускорить.
Наивный подход
Рассмотрим вариант при N = 3. Три треугольника, 9 вершин. Нумеруем вершины 0...8 и Перебираем все от 000 000 000 до 888 888 888.
Как видим, это очень дофига даже для трёх треугольников. Ну и повторы треугольников, которые тут будут постоянно попадаться, нам тут ни к чему.
Комбинаторный подход
Долгие вечера раздумий позволили голове родить следующую мысль:
Раз все треугольники должны быть склеены друг с другом хотя бы одним ребром, то максимальное количество вершин, которое понадобится для склейки из N треугольников, должно быть меньше, чем N * 3
И действительно, самая длинная валидная склейка будет выглядеть так:

И видно, что в ней всего 5 уникальных вершин вместо 9. В общем случае количество уникальных вершин получается по формуле N + 2, где N — количество треугольников. Если уникальных вершин будет больше, то один из треугольников обязательно будет соединяться с другими лишь одной вершиной, а это неправильно.
Итак. 5 уникальных вершин для трёх треугольников.
Всего комбинаций будет (вспоминаем комбинаторику и биномиальный коэффициент) 5! / (3!(5 — 3)!) = 10
Это количество уникальных треугольников, которое мы можем получить, генерируя все комбинации вершин.
Ну а теперь, считаем этот же биномиальный коэффициент для комбинаций из трёх треугольников
10! / (3!(10 — 3)!) = 120. Это сколько склеек надо перебрать чтобы учесть все варианты.
В общем виде формула для количества комбинаций выглядит следующим образом:
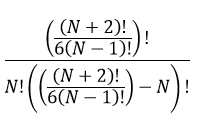
Видите, сколько факториалов? Например, для N = 10 всего будет 59 473 554 359 599 446 комбинаций, это очень много, даже если параллелить.
Когда я начал перебор с маленьких N (3,4,5..) то заметил, что программа довольно быстро находит все комбинации, а остальное — это просто дубликаты (они отсеиваются алгоритмом VF2, который проверяет графы на изоморфизм)
Довольно быстро — это значит, что последняя «хорошая» склейка для, например, N = 5 нашлась на 2084 шаге из 324 632, что составляет 0.642% от всего диапазона. Для N = 6 это 0.3644%. Последнее, что мне удалось посчитать самому — для N = 8 это 0.1352%.
То есть, в общем случае для N+1 мы смотрим, сколько процентов от предыдущего диапазона было посчитано и считаем столько же, это будет гарантировать нам, что всё проверено. Правда для N = 9 это все равно многовато (270 485 377 680, если проверять 0.1352%)
Так что, надо было придумать что то еще.
Итеративный подход
Еще несколько долгих вечеров и очередная идея:
А что, если генерить все склейки для N+1 на основе всех склеек для N путем добавления одного треугольника всеми возможными комбинациями?
То есть, мы знаем, что для троек у нас их всего две
[[A B C], [A B D], [A C D]]
[[A B C], [A B D], [A C E]]
А четверок шесть
[[A B C], [A B D], [A C D], [B C D]]
[[A B C], [A B D], [A C D], [B C E]]
[[A B C], [A B D], [A C E], [A D E]]
[[A B C], [A B D], [A C E], [A D F]]
[[A B C], [A B D], [A C E], [B C F]]
[[A B C], [A B D], [A C E], [B D F]]
Видно, что все четверки получились из предыдущих троек (перестановки генерятся в лексикографическом порядке)
Всё бы хорошо, генери себе дальше, НО! Когда проверил этот подход, обнаружилось, что таким образом генерятся не все, например, пятёрки
[[A B C], [A B D], [A C D], [B C E], [B D E]]
[[A B C], [A B D], [A C D], [B C E], [B D F]]
[[A B C], [A B D], [A C D], [B C E], [B E F]]
[[A B C], [A B D], [A C E], [A D E], [B C F]]
[[A B C], [A B D], [A C E], [A D F], [A E F]]
[[A B C], [A B D], [A C E], [A D F], [A E G]]
[[A B C], [A B D], [A C E], [A D F], [B C G]]
[[A B C], [A B D], [A C E], [A D F], [C E G]]
[[A B C], [A B D], [A C E], [B D E], [C D E]]
[[A B C], [A B D], [A C E], [B D F], [C E G]]
Если внимательно приглядеться, то предпоследняя пятерка получилась отличающейся от всех четверок не на один, а на два треугольника. В терминах топологии это «лента мёбиуса». И если попытаться нарисовать её без одного, любого треугольника, то будет получаться ситуация, когда группы треугольников соприкасаются лишь одной вершиной, что совсем нехорошо.
Что ж, выход все равно есть. Берем все получившиеся комбинации для N, отщипываем по одному треугольнику с конца, «догенериваем» еще все варианты двух и проверяем. Всё равно в кучу раз быстрее, чем с комбинаторным перебором.
Ан нет, при N = 8 нашлась триангуляция, которая отличается от всех семерок уже не на 2, а на 3 треугольника.
Так что, начиная с N = 9 отщипываются уже 2 треугольника, и «догенериваются» три. Это позволило просчитать почти все варианты вплоть до N = 11 и начало 12 ( почти — потому, что скорей всего там есть склейки, отличающиеся на 3, а то и больше треугольников). При том, что я распараллелил всё это дело. Один поток у меня выполняет первичную проверку склеек, остальные 3 занимаются отсечением дубликатов, т.к. проверка графов на изоморфность довольно ресурсоёмкое занятие.
В общем, если не нужны все варианты, то можно отщипывать (или не отщипывать) и догенеривать оставшиеся, это будет конечно плохо, но какие то варианты это способ точно даст даже для больших N. Потому, что совершенно непонятно сколько и когда надо «отщипывать» чтобы получить весь набор валидных склеек.
Но интересен то весь!
Я уже и на тему перебора графов материал искал, и чего только не думал, круче итеративного метода пока нет идей. Может быть у вас будут мысли на эту тему?
Например, когда генерируется комбинация треугольников, то первая всегда идет такая примерно склейка:
ABC ABD ABE ABF ABG…
Видно, что AB повторяется больше 2 раз. Если бы генерировать варианты, где изначально таких случаев бы не было, то по идее комбинаторному варианту было бы проще, но у меня нет идей как генерить такие последовательности.
P.S. это нужно для научной работы по классификации поверхностей. На меня конечно не обидятся, если я предоставлю данные до N = 11, у них и таких нет (хотя, например, тор можно построить из 14 треугольников, мне такое еще год обсчитывать). Но было бы интересно придумать способ который позволил бы это N отодвинуть подальше. Спасибо за внимание.
Автор: Scratch




