Познакомившись с магией систем компьютерной алгебры, я провела несколько вечеров в странных и на первый взгляд бессмысленных занятиях — перерешивая вузовские задачки по алгебре, математическому анализу, дифференциальным уравнениям… Просто потому, что было интересно — найдется ли такое уравнение, которое не смогут решить ни Maple, ни Maxima? В моем арсенале были эти две системы, и со всеми проблемами они справлялись «на ура». Это вовсе не означает, что всё решалось мгновенно и без применения математических знаний. Некоторые задачи требовали особых подходов, многочисленных преобразований и замен переменных. Так что, с противниками компьютерной алгебры можно поспорить — при правильном применении она нисколько не расслабляет , а наоборот — развивает логическое (и прочее)
Иллюстрируя вышесказанное, в этом посте я расскажу о нескольких различных сценариях использования СКА Maple в борьбе с интегралами. Надеюсь, что персоны, знакомые с тонкостями символьных вычислений, найдут для себя здесь что-нибудь новенькое. А для тех, кому такой способ решения задач в новинку, я постаралась добавить побольше комментариев.

Сценарий №1 — «Для ленивых/уставших»
Всем, кому не повезло с преподавателем матана, и людям, которым просто нравится наблюдать пошаговое решение интегралов, посвящен отдельный модуль пакета student. Некоторые его «фишки» хороши и для «заковыристых» интегралов, но об этом позже.
Итак, сначала подключим модуль и ограничим вывод дополнительной информации. Двоеточие на конце означает, что вывод команды будет скрыт от глаз пользователя.
> with(student):
> infolevel[Student[Calculus1]] := 1:Для разминки вычислим довольно обычный определенный интеграл, который был позаимствован из задачника по матанализу. Я предпочитаю использовать наиболее простой интерфейс (Classic Worksheet), в нем команды вводятся в символьной форме, а специальный интерфейс для ввода формул отсутствует. Получаем заботливо отрисованный интеграл.
> Res:=Int(1/(x^2+4*x+5),x=0..1);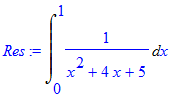
Мы могли бы просто использовать команду value(Res), и сразу получить результат. Но не зря же пакет student называется именно так! Займемся интегрированием по шагам. Сначала нам нужна подсказка.
> Hint(Res);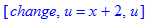
Предлагают замену переменных, чтобы избавиться от квадрата в знаменателе. Так и сделаем. Интеграл стал выглядеть гораздо приятней.
> Res:=Rule[change, u = x+2, u](Res);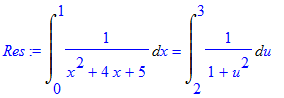
Теперь попробуем обойтись без подсказки.
> Res:=Rule[change, u = tan(v), v](Res);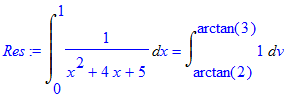
Интеграл от константы — что может быть проще? Здесь достаточно применить одно простое правило (полный список правил, разумеется, доступен в мануалах). И упростить.
> Result:=Rule[constant](Res);
> simplify(Result);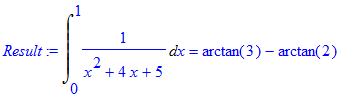
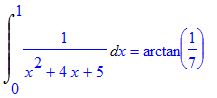
Сценарий №2 — «Для энтузиастов»
Попробуем теперь разобраться с двойным неопределенным интегралом, совсем без подсказок.
> DRes:=Doubleint(sqrt(sqrt(x^2+y^2)-x)/sqrt(x^2+y^2)*exp(-2*x-y),x=0..infinity,y=0..infinity);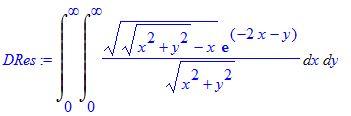
Очевидна замена переменных. С ней отлично справляется команда changevar. Для того, чтобы указать условия и избавиться от модулей, добавляем assuming.
> DRes:=changevar({x=r^2*cos(theta),y=r^2*sin(theta)},DRes,[theta,r]) assuming r>0;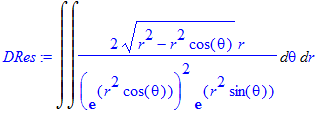
Упрощаем подынтегральное выражение (integrand) с помощью заветной команды simplify (она хороша для упрощения выражений — и не только внутри интегралов).
> IntegrandDRes:=simplify(integrand(DRes)) assuming r>0;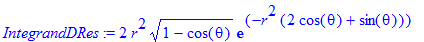
Избавляемся поочередно от обоих интегралов, не забывая про границы. Команда int — простая попытка проинтегрировать выражение. Она доступна и вне пакета student.
Res:= int(IntegrandDRes,r=0..infinity) assuming (theta>0,theta<Pi/2);
DRes:= int(Res,theta=0..Pi/2);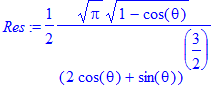
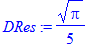
Ответ радует глаз. Если не радует, можно представить его в виде дроби с заданной точностью.
> evalf[16](DRes);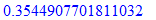
Заключение
Я затронула лишь малую часть возможностей, которые предоставляют символьные вычисления. Но даже владея небольшим набором команд и правильно комбинируя их, можно решить много интересных примеров и поупражняться в знании математических правил и законов. Предпочтения в выборе программного пакета, по моему мнению, не играют решающей роли, ведь синтаксически все системы достаточно похожи друг на друга.
А вот с литературой по системам компьютерной алгебры дела обстоят плохо. Это касается и Maple: большая часть книг написаны уже давно и не соответствуют возможностям новых версий ПО. Поэтому лучшее, что можно прочесть для ознакомления с возможностями различных пакетов и функций — это неисчерпаемый официальный мануал.
Автор: cloudberry






