Добрый день, любезные читатели. Как, быть может, некоторые из вас помнят, в предыдущем посте я грозился показать, как конструируется нормальное число, доказательство нормальности которого возможно провести элементарными средствами. К сожалению, у меня целый месяц не было возможности написать этот пост вследствие неожиданного перехода моего аккаунта в режим рид-онли. Однако теперь я вернулся, так сказать, отдохнувшим и могу приступить к выполнению обещания.
Если вы знаете, что такое нормальные числа, и вам интересно, как их строить — пожалуйте под кат. Если вы не знаете, что такое нормальные числа — прочитайте предыдущую статью (ссылка выше), затем пожалуйте под кат. Если же вам неинтересно, как строить нормальное число — всё равно пожалуйте под кат, потому что там я буду рассказывать про циклы де Брёйна, которые сами по себе очень интересные штуки.

Цирк дрессированных структур имени Николаса де Брёйна.
Товарищ де Брёйн (он же де Бройн, де Брюйн и даже иногда де Брюин) — это, конечно, не Гаусс и не Эйлер, но персоналия также достаточно значимая. Среди меня он наиболее известен по результатам в области комбинаторики и теории графов, однако, говорят, он занимался и чем-то ещё. Впрочем, в рамках данной статьи его достижениями в иных сферах можно цинично пренебречь.
Циклом де Брёйна для некоторых натуральных параметров n и k называется циклическая последовательность из kn цифр k-ичной системы счисления, в которой (последовательности) любая возможная подпоследовательность длины n встречается ровно единожды.
Рассмотрим примеры циклов де Брёйна для различных k и n.
n=1, k=2: последовательность «01» будет искомым циклом, поскольку содержит по одному разу все возможные двоичные последовательности длины 1 (то есть нолик и единичку).
n=2, k=2: последовательность «0110» нам подходит. Проверим: в ней содержатся подпоследовательности «01», «11», «10» и, благодаря цикличности, «00». Это все возможные двоичные последовательности длины 2.
n=3, k=10:
0370380390410420430440450460470480490510520530540550560570580590610620630640650660670680690710720730
7407507607707807908108208308408508608708808909109209309409509609709809911121131141151161171181191221
2312412512612712812913213313413513613713813914214314414514614714814915215315415515615715815916216316
4165166167168169172173174175176177178179182183184185186187188189192193194195196197198199222322422522
6227228229233234235236237238239243244245246247248249253254255256257258259263264265266267268269273274
2752762772782792832842852862872882892932942952962972982993334335336337338339344345346347348349354355
3563573583593643653663673683693743753763773783793843853863873883893943953963973983994445446447448449
4554564574584594654664674684694754764774784794854864874884894954964974984995556557558559566567568569
5765775785795865875885895965975985996667668669677678679687688689697698699777877978878979879988898999
Вообще, вот тут, например, есть онлайн-генератор циклов де Брёйна для любых не слишком больших параметров.
По слухам, использование циклов де Брёйна может сократить время брутфорса, если ломаемое устройство в качестве PIN-кода воспринимает n последних введённых символов. Вместо того, чтобы вводить по очереди все kn возможных кодов (что даст n*kn символов), можно ввести последовательность цифр некоторого цикла де Брёйна (что даст kn символов) с небольшим «хвостиком» (n — 1 символ, чтобы замкнуть цикл). Итого выигрыш по времени приблизительно в n раз. Впрочем, я никогда не встречался с такими устройствами, поэтому для меня это просто слухи. Если вам есть что сказать по этому поводу, отпишитесь, пожалуйста, в комментариях, мне будет интересно.
Первый вопрос, который должен возникнуть у математика после прочтения вышеизложенного: «Для любых ли k и n существует соответствующий им цикл де Брёйна?» Первый вопрос, который должен возникнуть у программиста:«Каким образом можно генерировать цикл де Брёйна для заданных k и n?» Чтобы ответить на оба этих вопроса, введём новое определение.
Графом де Брёйна для натуральных параметров k и n называется ориентированный граф, вершинам которого соответствуют все возможные n-значные k-ичные последовательности, а рёбра соединяют те и только те пары вершин, для которых последние n-1 цифр первого числа совпадают с первыми n-1 цифрами второго числа.
Очевидно, что найдя в этом графе гамильтонов цикл (т.е. замкнутый путь по его рёбрам, проходящий через каждую вершину ровно один раз), мы тем самым найдём и цикл де Брёйна для тех же параметров k и n (далее будем использовать сокращённое обозначение B(k, n) ), и наоборот. Действительно, цикл де Брёйна — это, по сути, «склеивание» всевозможных n-значных последовательностей по их общим (n-1)-значным подпоследовательностям. Однако гамильтонов цикл в графе де Брёйна как раз и предоставляет такой способ «склейки».
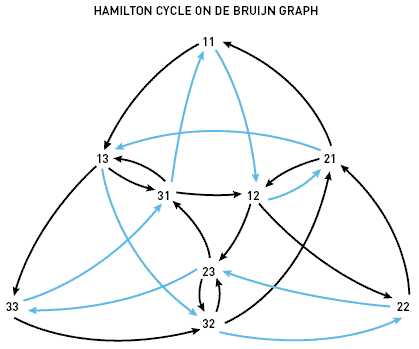
Таким образом мы ответили на вопрос программиста. Если B(k, n) существует, мы можем найти её соответствующим алгоритмом на соответствующем графе. Однако математик не удовлетворён. Существование гамильтонова цикла — вещь совершенно неочевидная, а значит, неочевидно, существует ли B(k, n). Однако, к счастью для математика, есть ещё одно замечательное свойство графа де Брёйна: всякий эйлеров (т.е. проходящий через все рёбра) цикл соответствует некоторому циклу де Брёйна B(k, n+1). Действительно, каждое ребро графа де Брёйна — это пара «склеенных» n-значных последовательностей, что можно интерпретировать как одну (n+1) — значную последовательность. Если одно ребро входит в вершину, из которой выходит второе — значит, (n+1)-значные последовательности, соответствующие этим рёбрам, «склеиваются» по общей n-значной последовательности, соответствующей этой вершине.
Существование эйлеровых циклов — вопрос хорошо изученный; критерий наличия эйлерова цикла можно найти, например, в википедии:
Ориентированный граф содержит эйлеров цикл тогда и только тогда, когда он сильно связан и для каждой вершины графа её полустепень захода равна её полустепени исхода, то есть в вершину входит столько же ребер, сколько из неё и выходит.
Сильная связность — это когда для любой пары вершин в ориентированном графе мы можем из одной попасть в другую, следуя по рёбрам, и наоборот. Полустепень захода — это сколько рёбер входит в вершину. Полустепень исхода — это, соответственно, сколько рёбер из неё выходит. Предлагаю читателю самостоятельно доказать, что граф де Брёйна удовлетворяет условию существования эйлерова цикла. Серьёзно, если у вас есть свободное время, которое нечем занять. напишите доказательство в комментариях.
Скажем «нет» графомании
Всё-таки искать циклы де Брёйна с помощью алгоритмов на графах не слишком удобно, да и грешновато. Существуют более эффективные способы построения оных циклов. Здесь я расскажу об одном из них: с помощью ожерелий. Самые любознательные могут почитать оригинальную статью, я же изложу всё кратко и бездоказательно.
Ожерельем называется конечная последовательность, рассматривая с точностью до циклического сдвига. То есть «1100», «1001», «0011» — это одно и то же ожерелье. С ожерельями связано много любопытных комбинаторных результатов, однако сейчас мы не будем на них отвлекаться.
Представителем ожерелья мы назовём ту его запись, которая идёт раньше всех остальных записей в лексикографическом порядке. Ожерелье из предыдущего примера можно записать четыремя способами: «1100», «1001», «0011», «0110». Из них раньше всего «по алфавиту» идёт запись «0011», она-то и будет представителем.
Периодической редукцией последовательности назовём наименьшую её подпоследовательность такую, что исходная последовательность состоит из некоторого числа её повторений. Например «0101» — это «01», повторённая два раза, поэтому подпоследовательность «01» — это периодическая редукция последовательности «0101». Периодической редукцией последовательности «0000» будет подпоследовательность «0». Большинство последовательностей нельзя представить в виде повторения некоторого меньшего «куска», поэтому их периодические редукции совпадают с ними самими.
Теперь, сформулировав эти понятия, я могу записать алгоритм построения B(k, n) с помощью ожерелий:
- Берём все возможные k-ичные ожерелья длины n;
- Для каждого из них выбираем представителя;
- Выписываем представителей в лексикографическом порядке;
- Каждого представителя заменяем его периодической редукцией;
- ???
- Мы построили B(k, n).
Опробуем этот алгоритм на примере B(2,3). У нас есть всего четыре двоичных ожерелья длины три: из всех единичек, из всех ноликов, из одной единички и двух ноликов, из одного нолика и двух единичек. Их представителями будут, соответственно, «111», «000», «001», «011». Упорядочим их по алфавиту: «000», «001», «011», «111». После периодической редукции получаем «0», «001», «011», «1». Конкатенация этих четырёх бинарных слов — «00010111» — как раз и будет B(2,3). Можете проверить это, можете поверить моему честному слову.
Вернёмся к нашим баранам
Так вот, построение нормального числа. Этот параграф будет очень коротким. Чтобы построить k-ичное число, в нормальности которого нет никаких сомнений, возьмём в качестве записи его дробной части бесконечную конкатенацию: B(k, 1) + B(k, 2) +… + B(k, n) +…
В принципе, на этом данный псто можно было бы и закончить, но на всякий случай поясню. Любая последовательность длины m входит в B(k, n), n ≥ m, ровно с той же частотой, что и любая другая последовательность длины m. Это как раз то, что нужно для нормального числа. Соответственно, погрешности в частоте могут возникнуть либо при n < m (а это начальный кусок конечной длины, он не может повлиять на асимптотическую плотность), либо на «стыках» между циклами де Брёйна.
Поскольку при увеличении n длина цикла де Брёйна растёт экспоненциально, асимптотическая плотность стыков равна нулю, а значит, стыки также не могут повлиять на асимптотическую плотность нашей последовательности. Вывод: в записи построенного нами числа для всякого n все последовательности длины n будут встречаться с одной и той же асимптотической плотностью. Это определение нормального числа. Можно кричать «ура» и бросать в воздух чепчики: теорема доказана.
Автор: Sirion





