Для начала небольшой спойлер

Да я знаю, что если написать фамилию с заглавной буквы, казуса не получится. Дальше перевод.
Математика – одна из немногих областей знаний, которая может быть объективно названа истинной, потому что ее теоремы основаны на чистой логике. Но в то же время эти теоремы часто оказываются очень странными и противоречащими интуиции.
Некоторые люди считают математику скучной. Следующие примеры показывают, что она какая угодно, но не такая
5. Случайные наборы данных
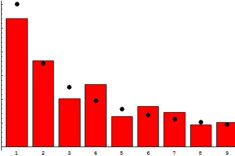
Как это ни странно, случайные данные на самом деле не такие уж и случайные. В приведенных данных, представляющих собой все от биржевых курсов до населения городов, высот зданий и протяженностей рек, около 30 процентов всех чисел начинаются с единицы. Меньшее количество начинается с 2, еще меньше с 3 и так далее, с 9 начинается только каждое двадцатое число. И чем больше набор данных, чем шире порядок охватываемых величин, тем сильнее проявляется эта закономерность.
4. Спирали простых чисел
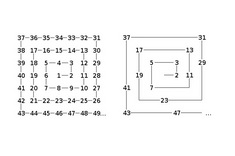
В силу того, что простые числа неделимы (кроме как на единицу и самого себя), и того, что все остальные числа могут быть представлены в виде их произведения, простые числа часто рассматриваются как «атомы» в мире математики. Несмотря на свою важность, распределение простых чисел до сих пор остается тайной. Нет такого правила, которое бы однозначно говорило, какие числа будут простыми и через сколько встретится следующее простое число.
Кажущаяся случайность простых чисел делает факты, обнаруженные в «Скатерти Улама» очень странными.
В 1963 году математик Станислав Улам, обнаружил удивительную закономерность, когда разрисовывал свою записную книжку во время презентации: если записывать целые числа по спирали, простые числа выстраиваются вдоль диагональных линий. Само по себе это не очень удивительно, если помнить, что все простые числа, кроме двойки, нечетные, а диагональные линии в спиралях целых чисел поочередно являются нечетными. Более необычной была тенденция простых чисел лежать преимущественно на одних диагоналях и практически отсутствовать на других. Причем закономерность наблюдалась вне зависимости от того, с какого числа начиналась спираль (с единицы или любого другого).
Даже если масштабировать спираль, чтобы она вмещала гораздо большее количество чисел, можно увидеть, что скопление простых чисел на одних диагоналях гораздо плотнее, чем на других. Существуют математические предположения, объясняющие эту закономерность, но пока они не доказаны.
3. Выворачивание сферы
В одной важной области математики, которая называется топология, два объекта считаются эквивалентными или гомеоморфными, если один из них может быть преобразован в другой путем скручивания или растягивания поверхности. Объекты считаются разными, если для преобразования требуются разрезы или изломы поверхности.

В качестве примера рассмотрим тор – объект в форме пончика. Если поставить его вертикально, расширить одну сторону и вдавить верхушку этой же стороны, то получится цилиндрический объект с ручкой. В среде математиков существует классическая шутка, что топологи не могут отличить пончика от чашки с кофе.
С другой стороны, ленты Мебиуса – петли с единственным перегибом не являются гомеоморфными петлями без перегибов (цилиндры), потому что нельзя распрямить ленту Мебиуса, без того чтобы разрезать ее, перевернуть одну сторону и склеить заново.
Топологов давно интересует вопрос, будет ли сфера гомеоморфной самой себе, будучи вывернутой наизнанку? Другими словами, можно ли выворачивать сферу? На первый взгляд это кажется невозможным, потому что нельзя проткнуть дырку в сфере. Но, оказывается, выворачивание сферы возможно. Как это делается, показано на видео
.
Поражает тот факт, что тополог Бернард Морин, который является главным разработчиком приведенного метода выворачивания сферы, слеп.
2. Математика стен

Несмотря на то, что стены могут быть украшены бесконечным количеством завитушек, говоря математическим языком, существует конечное число отдельных геометрических шаблонов. Все периодические рисунки Эшера, обои, плиточные дизайны и вообще все двумерные повторяющиеся группы фигур, могут быть отнесены к той или иной так называемой «группе рисунка обоев». И знаете, сколько существует таких групп? Ровно 17.
1. Сонет
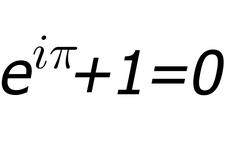
«Как сонет Шекспира схватывает саму суть любви, или картина показывает внутреннюю красоту человека, уравнение Эйлера проникает в самые глубины существования.»
Математик из Стэнфорда Кейт Девлин (Keith Devlin) написал эти слова об уравнении в эссе 2002 года, которое называлось «Самое прекрасное уравнение». Но почему от формулы Эйлера перехватывает дыхание? И что она вообще значит?
Во-первых, буква «e» представляет собой иррациональное число (с бесконечным количеством цифр), которое начинается с 2.71828… Открытое в контексте непрерывно начисляемого сложного процента, оно описывает темпы экспоненциального роста от колоний популяций насекомых до радиоактивного распада. В математике число обладает рядом неожиданных свойств, например, оно равняется сумме обратных факториалов от нуля до бесконечности. В конечном счете константа e оккупировала математику, взявшись вроде бы ниоткуда, но оказавшись в большом числе важных уравнений.
Далее. i представляет собой так называемую мнимую единицу – квадратный корень из минус 1. «Так называемую», потому что в реальности не существует числа, которое, будучи умноженным само на себя, в результате дало отрицательное число (потому отрицательные числа не имеют действительных квадратных корней). Но в математике существует большое количество ситуаций, когда приходится извлекать квадратный корень из отрицательного числа. Число i используется как своеобразная пометка того места, где такая операция была произведена.
Пи – отношение длины окружности к ее диаметру, одна из любимых и наиболее интересных констант в математике. Подобно e, она появилась в большом количестве математических и физических формул как будто из ниоткуда.
Константа e, возведенная в степень мнимая единица, умноженная на Пи равняется минус одному. Из уравнения Эйлера следует, что добавление к этому единицы дает ноль. Трудно поверить, что все эти странные числа, одно из которых даже не относится к реальному миру, могут быть так просто скомбинированы. Но это доказанный факт.
Автор: vadim_ig






