Здравствуйте.
Сомневаюсь в своей готовности писать полноценные содержательные посты. Но хотел бы иметь возможность комментировать и задавать вопросы.
В последнем посте из R-хаба «Визуализация двумерного гауссиана на плоскости» был описан алгоритм построения доверительного эллипса по ковариационной матрице. Алгоритм сопровождался примером и R-скриптом.
Возможно, автору поста о «Визуализации гауссианы» mephistopheies и читателям R-хаба будет полезной следующая информация. В репозитории R есть пакет ellipse. Этот пакет содержит различные процедуры для построения эллипсов доверительных областей.
Рассмотрим пример.
Выборка из двумерного нормального распределения
Для генерации выборки из двумерного нормального распределения используем пакет mvtnorm.
Строим выборку data из 1000 элементов c вектором средних значений mu и ковариационной матрицей sigma:
require(mvtnorm)
mu <- c(1,2)
sigma <- matrix(c(4,2,2,3), ncol=2)
set.seed(100)
data <- rmvnorm(n=1000, mean=mu, sigma=sigma) # генерируем выборку с заданными параметрами
Эллипс 95% доверительной области
Для ковариационной матрицы sigma находим координаты 100 точек эллипса 95% доверительной области:
require(ellipse)
confidence.ellipse <- ellipse(sigma,centre=mu,level=0.95,npoints=100)
Визуализация
Отображаем на плоскости точки data и эллипс confidence.ellipse
plot(data,pch=19,col=rgb(0, 0.5, 1, 0.2), xlab="x", ylab="y",
xlim=range(data[,1]), ylim=range(data[,2]))
par(new=TRUE)
plot(confidence.ellipse,type="l", xlab="",ylab="",
xlim=range(data[,1]),ylim=range(data[,2]))
Результат:
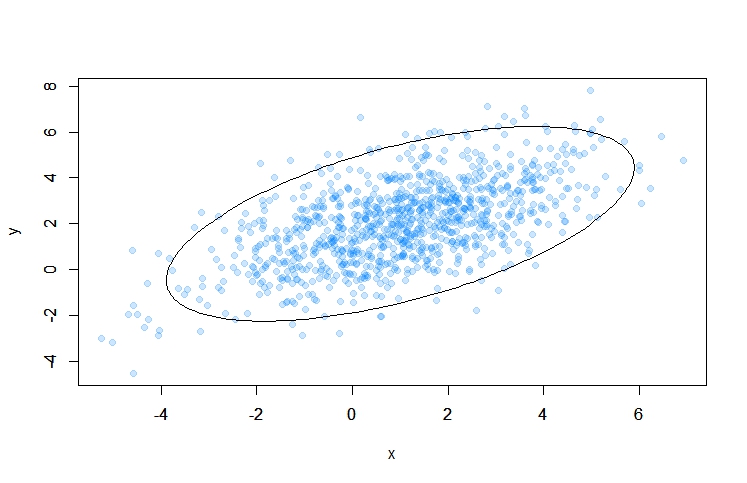
Автор: jzha






