CFD 3D: простой симулятор воды

Введение

CFD (Computational fluid dynamics) — вычислительная гидродинамика.
Используется для моделирования разных процессов в жидкостях, а также разных типов жидкостей (например мёд, нефть — это все жидкости).

В данном посте рассматривается 2D симулятор обычной воды с открытой поверхностью и препятствиями (для 3D версии все аналогично + доступны исходники).
Поверхность воды представляет собой границу, отделяющую воду от воздуха.Это позволяет моделировать волны, падение капель и т.д.

Написать свой симулятор я решил по нескольким причинам. Одна из них — это отсутствие нормально написанных исходников по данной теме в интернете. Все что я находил, было или на фортране, или только 2d, или написано очень сложно для понимания.

Итак, основные фичи симулятора:

• real-time режим
• простая и понятная схема расчета + explicit, implicit
• открытый исходный код
• есть и 2d и 3d
• встроенный простой opengl render
• xml описание сцен

В плане расчетов я отталкивался от уравнений Навье-Стокса (а также от найденных в инете исходников).
Это система дифференциальных уравнений в частных производных, описывающая движение вязкой несжимаемой жидкости. Слово несжимаемой здесь скорее для галочки, поскольку все жидкости по определению являются несжимаемыми. Вязкость обозначает трение между отдельными частицами, она не дает разлетаться им в разных направлениях как в случае с газом, когда он заполняет весь отведенный ему объем. Частицы жидкости же стараются держатся по возможности вместе.

В своем симуляторе я использовал немного измененный набор уравнений, об этом ниже…

Уравнения гидродинамики

Итак, вот основные уравнения Навье-Стокса в общем (векторном) виде:

Здесь:

• u — это традиционное обозначение поля скорости ( в 2D — скорость состоит из 2-х компонент по x и по y направлениям — обозначаются они соответственно как u и v)
• p — это давление
• t — время
• символ rho — плотность жидкости
• символ mu — кинематический коэффициент вязкости
• Fext — какие-либо внешние силы действующие на жидкость, например гравитация ( g )

Первое из уравнений — уравнение движения, второе — уравнение неразрывности.
Уравнение движения выглядит похожим на уравнение Ньютона ma=F, где у нас справа — сумма сил действующих на жидкость — это давление, диффузия, гравитация…

Для 2D варианта уравнения принимают такой вид (здесь уже они представлены в безразмерном виде):

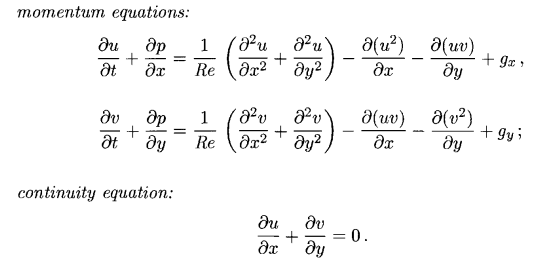
Уравнение движения теперь представлено 2 уравнениями — для 2х компонентов скорости — u и v.
По поводу нового коэффициента Re — это число Рейнольдса (оно получилось при переходе к безразмерным переменным), которое заменяет сразу 2 предыдущих коэффициента — коэфф. плотности и вязкости. От него зависит на что будет похожа вода — на мед или на обычную воду. Чем больше Re тем более похожа жидкость на обычную воду.
В скобках это у нас выражение определяющее вязкое поведение жидкости (или диффузия). Остальные члены в правой части (кроме гравитации) — это конвекция. В левой части — скорость и давление.

Далее я немного упростил эти уравнения:

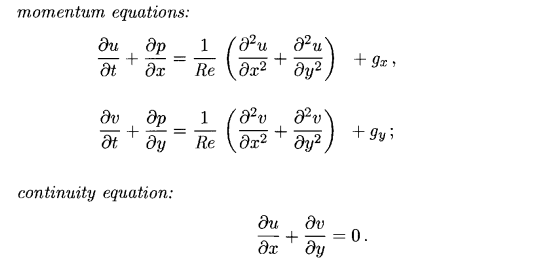
Как видно — исчезла конвекция, что несколько ухудшает поведение жидкости, но в целом визуально выглядит вполне нормально.Отсутствие конвекции дает сразу несколько плюсов — исчезает нелинейность, улучшается стабильность и шаг по времени можно делать больше, также конвекция обычно очень затратный терм по количеству необходимых вычислений, к тому же чтобы правильно дискретизировать конвекцию- применяют специальные схемы — что выглядит достаточно громоздко.

При решении уравнений применяется специальная схема, называемая Splitting.Очень хотелось бы остановиться поподробней на этом, но это скорее для отдельного поста.Тема достаточно большая.Очень хорошо это описано в книге
Bridson R. Fluid Simulation for Computer Graphics.pdf в разделе Overview of numerical simulation.
И тут Numerical simulation in fluid dynamics Griebel M Dornseifer T Neunhoeffer T SIAM 1998

Вот split схема решения уравнений:

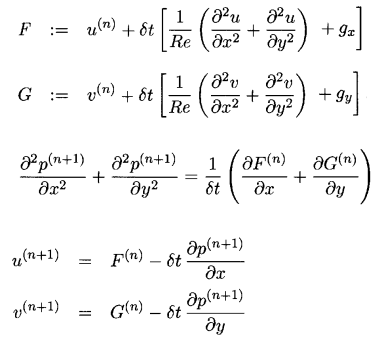
Для шага по времени используется метод Эйлера, также на первом шаге мы опускаем давление и получаем промежуточный расчет скоростей F и G. Эти скорости, кроме того что не учитывают давление, еще и не будут удовлетворять уравнению неразрывности. Путем хитрых манипуляций находится уравнение для расчета давления, которое в том числе решает и проблему с уравнением неразрывности. Решая это уравнение по уже рассчитанным F и G мы находим новое давление P.
Далее на 3-м шаге происходит коррекция скоростей с учетом посчитанного давления.
На этом завершается один полный шаг по времени и на следующем шаге все повторяется заново.

Дискретизация уравнений

Для дискретизации уравнений используется метод конечных разностей. Для шага по времени используется стандартный метод Эйлера — схематично выглядит это так: u(n+1)=u(n) + dt* f,
где под f понимается вся часть уравнения в которую не входит дифференциал по времени.

В общем значение скорости в новый момент времени ( u(n+1) ) находим из значения в предыдущий момент времени ( u(n) ).
Описывать дискретные аналоги уравнений в данном посте я не буду.Это очень хорошо сделано в книге «Numerical simulation in fluid dynamics» (Griebel M Dornseifer T Neunhoeffer T SIAM 1998).

Для решения дискретных уравнений используется не матричный способ решения а итеративный — Гаусс-Зейделя. Он не требует предварительной сборки матриц и вообще не требует никаких промежуточных массивов, позволяет легко модифицировать расчетную схему, приблизительное решение находиться уже через 1 итерацию — что очень ускоряет всю симуляцию.

В данном посте будет рассмотрен 2D случай, основной акцент будет на объяснении граничных условий, т.к. они вызывают наибольшие сложности в решении уравнений. Вся симулируемая область разбивается на imax точек по горизонтали и jmax по вертикали. Получается сетка imax*jmax клеток.
К ним с 4 границ добавляются граничные точки. Итого получается массив размером (imax+2)*(jmax+2).

У каждой клетки свои значения скоростей и давления — принято говорить о векторном поле скоростей и скалярном поле давления на расчетной сетке.
U — скорость частицы в клетке по x
V — скорость частицы в клетке по y
P — давление

Обычно принято располагать расчетные переменные (U,V,P) по центру клеток, но в случае с моделированием жидкости это всегда вызывает проблемы с решением — оно получается не совсем корректное и осциллирующее. Поэтому в CFD используется разнесенная сетка (staggered grid) — еще ее называют чехарда.

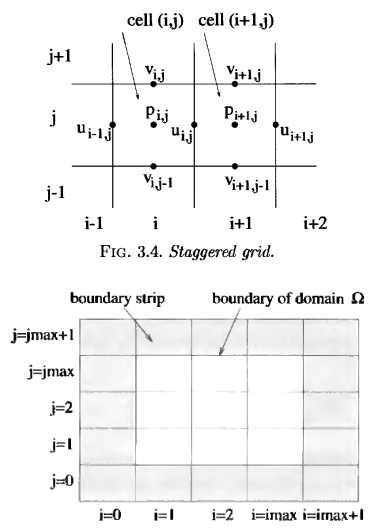
Из рисунка видно что скорости находятся не в самой клетке а на ее гранях, u — на правой границе клетки, а v — на верхней границе.

Граничные условия на стенках

Для расчета методом конечных разностей, нам нужно задать значения (u,v,p) на границах раcчетной сетки.Это 4 стенки — слева справа снизу и сверху.Граничные условия могут быть типов no-slip и free-sleep; есть и другие типы, но это скорее специализированные условия, а не общего плана.

free-sleep — это значит что жидкость свободно скользит по стенке, как будто отсутствует трение и ничто ей не мешает двигаться вдоль неё.
В данном посте мы не рассматриваем этот тип граничных условий.

no-slip — это условие прилипания — то есть жидкость притормаживает когда натыкается на стенку.
Это означает, что скорость жидкости совпадает со скоростью стенки (то есть в нашем случае равна нулю на неподвижной границе).

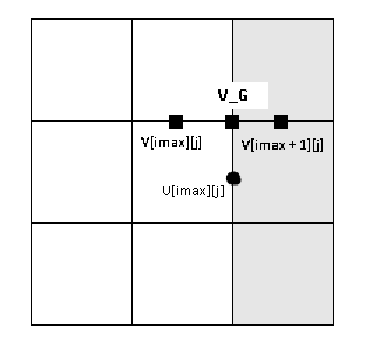
Рассмотрим для примера только правую границу: u составляющая скорости = 0, т.к. она перпендикулярна стенке и вода не должна проникать сквозь границу.
v составляющая для случая no-slip границы тоже равна 0, но для нашей staggered сетки придется ее скорректировать.Для v составляющей, учитывая что v не находится прямо на границе, необходимо немного подправить выражение.
v на стенке будет равно среднему между 2-я последними ячейками. v_g=(v[imax+1][j]+v[imax][j])/2
v_g приравняем нулю ( (v[imax+1][j]+v[imax][j])/2=0 ) и найдем отсюда значение v[imax+1][j], которое нам и нужно задать в программе:
v[imax+1][j]=-v[imax][j];
Тоже самое необходимо проделать для u компоненты на верхней границе.

4 границы представлены в массиве следующими координатами:

левая стенка

u[0][j], где j пробегает значения по всей стенке
v[0][j]

Вот как это выглядит в коде:

for (j = 0; j <= jmax + 1; j++)
{
  U[0][j] = 0.0;
  V[0][j] = -V[1][j];
}

нижняя стенка

u[i][0]
v[i][0]

for (i = 0; i <= imax + 1; i++)
{
  U[i][0] = -U[i][1];
  V[i][0] = 0.0;
}

правая стенка
Т.к у нас разнесенная сетка, то на правой стенке у нас граница для значений u проходит не по последнему столбцу а по предпоследнему — поэтому ставим значения для U в клетке — U[imax][j].

u[imax][j]
v[imax+1][j]

for (j = 0; j <= jmax + 1; j++)
{
  U[imax][j] = 0.0;
  V[imax + 1][j] = -V[imax][j];
}

верхняя стенка
Здесь уже для значений v граница проходит по предпоследней строке — jmax — поэтому ставим значения для V в клетке — V[i][jmax]

u[i][jmax+1]
v[i][jmax]

for (i = 0; i <= imax + 1; i++)
{
  U[i][jmax + 1] = -U[i][jmax];
  V[i][jmax] = 0.0;
}

Для тестирования основного решателя можно все граничные значения задать =0.

Также нам нужно проставить давление на границах.Давление задано по центру клеток а не по краям как скорости.Поэтому с ним все очень просто.Давление на границах можно поставить таким же как и в соседних клетках.Просто копируем значения из соседних клеток.

for (j = 1; j <= jmax; j++)
{
  // левая стенка
  P[0][j] = P[1][j];
  // правая стенка
  P[imax + 1][j] = P[imax][j];
}
for (i = 1; i <= imax; i++)
{
  P[i][0] = P[i][1];
  P[i][jmax + 1] = P[i][jmax];
}

Граничные условия на препятствиях

Препятствия представлены флагом C_B. Граничные условия для них ставятся по такому же принципу как и для внешних стенок.Приведу 2 примера простановки давления:

if (IsObstacle(i, j))
{
   // если снизу от препятствия - вода - то копируем значение P из нее
          if (IsFluid(i, j - 1))
          {
            P[i][j] = P[i][j - 1];
          }
   // если слева - вода ...
          else if (IsFluid(i - 1, j))
          {
            P[i][j] = P[i - 1][j];
          }
  // .......
}

Для угловой клетки берем среднее по значениям окружающих ее водных клеток.Например возмём препятствие, слева и сверху от него будет вода.Тогда давление в клетке-препятствии считаем так:

if (IsFluid(i - 1, j) && IsFluid(i, j + 1))
{
  P[i][j] = (P[i][j + 1] + P[i - 1][j]) / 2;
}

Граничные условия на поверхности

Поверхность и ее движение моделируется с помощью частиц. (Исходники с граничными условиями на поверхности, сделанные как описано в данном разделе — находятся в папке simpletestobstacle.)

Изначально частицы помещаются в клетки с жидкостью по 4 штуки на клетку (по 1 возле каждого угла). Далее частицы на каждом шаге перемещаются используя простой метод Эйлера из классической механики. Скорости для движения берутся в каждой клетке как средние по всей клетке(хотя не проблема использовать например интерполяцию).

  x = particles[k].x;
  y = particles[k].y;
// определяем координаты клетки в которой находятся частицы
  i = (int)(x / delx);
  j = (int)(y / dely);
  u = U[i][j];
  v = V[i][j];
  // собственно сам метод Эйлера для движения частиц
  x += delt * u;
  y += delt * v;

На каждом шаге клетки с частицами помечаются как вода.Остальные — это пустые клетки, в них расчет основных переменных (u,v,p) не производится.

Для расчетов основных переменных, необходимо задать граничные условия на поверхности и соседними с ней клетками, также как это требовалось для стенок. Но сначала нужно определить какие клетки, из помеченных как вода — принадлежат к поверхности, а также с какой стороны находится воздух. Для этих целей используется 2 массива — FLAG и FLAGSURF. В первом задаются только типы клеток — вода, воздух (пусто) и препятствия. Вот соответствующие флаги (сокращения B — boundary F — fluid E — empty):

public const int C_B = 0x0000; //препятствие
public const int C_F = 0x0010;//вода
public const int C_E = 0x1000;//пусто

Массив FLAGSURF используется для определения поверхностных клеток, для остальных клеток значение там =0. Флаги в этом массиве определяют не только тип клетки, но и все комбинации соседних клеток, в которых пусто. Флаги сделаны как стандартные битовые маски, чтобы их можно было комбинировать.
Каждое значение в FLAGSURF содержит 4 бита которые соответствуют 4 сторонам (соседним клеткам).
Если бит установлен в 1 то в соответствующей соседней клетке — пусто. Если 0 — то там вода.
Расположение битов: 0000 NSWO 0000 0000 — буквами обозначены 4 стороны N (North север) S (South юг) W (West восток) и O (запад).

Весь список флагов есть в исходниках, поэтому приведу лишь некоторые примеры значений:

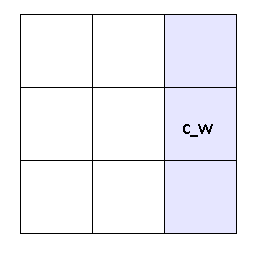
public const int C_W = 0x0200;// 512
в двоичном виде значение выглядит так 0000 0010 0000 0000
Здесь флаг соответствующий стороне W установлен в 1. Это значит что слева от текущей клетки — пусто.
В тоже время остальные 3 бита установлены в 0 — значит остальные соседние клетки наполнены водой.

public const int C_SW = 0x0600;// 1536 0000 0110 0000 0000
Здесь флаг соответствующий сторонам W и S установлен в 1. Значит слева и снизу от текущей клетки — пусто, а остальные клетки — водные

При определении типов поверхностных клеток и заполнении массива FLAGSURF соответствующие биты устанавливаются в 1 таким образом:

// если слева пусто, то установим соответствующий бит  в 1
if (FLAG[i-1][j] == GG.C_E)
  FLAGSURF[i][j] = FLAGSURF[i][j] | GG.C_W;

Массив FLAGSURF в основном нужен только для удобства простановки граничных условий на поверхности. Поскольку для разных типов поверхностных клеток применяются разные граничные условия. Как уже говорилось, нам необходимо проставить граничные условия в пустых клетках, которые находятся рядом с поверхностными клетками и также граничные условия нужны в самих поверхностных клетках, поскольку у нас staggered сетка и в расчет переменных u v входят не все поверхностные клетки.

Принцип простановки значений простой. Т.к. давление воздуха в 1000 раз меньше давления в воде — то им можно пренебречь и дать возможность воде свободно перемещаться вдоль поверхности, никак не ограничивая ее скорости и не изменяя направления движения. Конечно в моей схеме не учитывается поверхностное натяжение, иначе все было бы гораздо сложней.

Мы проставляем значения скоростей U и V в поверхностных клетках и граничащих с ними пустых клетках не забывая при этом то, что у нас staggered сетка.
Значения для простановки берутся из соседних водных клеток.Осталось только решить из каких именно соседних клеток все это берется, потому что таких клеток может быть несколько.

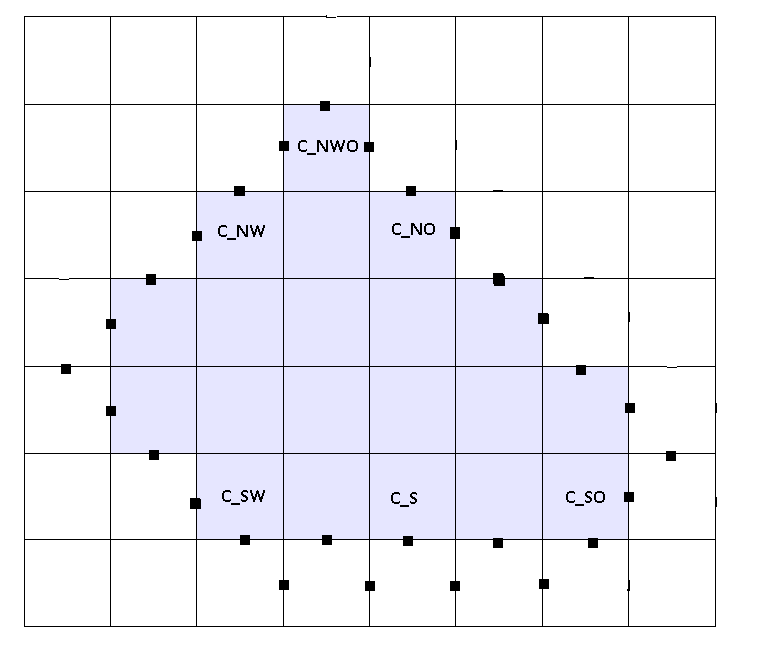
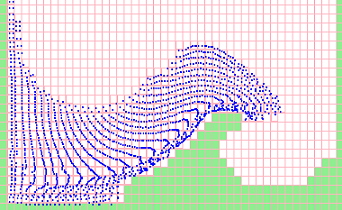
Вот скрин с граничными условиями которые нужно проставить.Синие квадраты — вода. Черные метки — требующиеся граничные условия. Обратите внимание что метки расположены частично в поверхностных клетках а частично в пустых. Так получается, потому что в коде решателя у нас есть такие условия (как видно — в клетках перед правой граничной стенкой расчет U V не производится):

        if (IsFluid(i, j) && IsFluid(i+1, j)){
          F[i][j] = ...
        }

Рассмотрим несколько примеров:

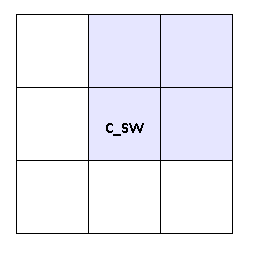
клетка с флагом C_SW

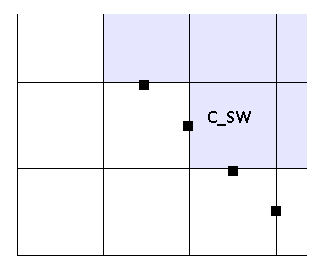
          case GG.C_SW:
            {
              U[i][j - 1] = U[i][j];
              V[i][j - 1] = V[i][j];
              U[i - 1][j] = U[i][j];
              V[i - 1][j] = V[i][j];
            } break;

Здесь значения в самой клетки нам не нужны — они будут рассчитаны в решателе. Но зато нужны значения в соседних пустых клетках — т.к. в решателе есть термы с U[i][j — 1] и т.д.

Ближайшая водная клетка к этим пустым клеткам — это клетка [i][j] из нее и берутся значения U и V.
Из рисунка видно, что значение для V[i — 1][j] можно было бы взять как из клетки [i][j], так и из [i — 1][j+1] — но в общем случае клетка [i — 1][j+1] может оказаться не водной к тому же значение V в ней может тоже оказаться граничным и еще не будет проставлено.Поэтому правильный вариант — [i][j] т.к значения в ней будут рассчитаны в решателе.

клетка с флагом C_W

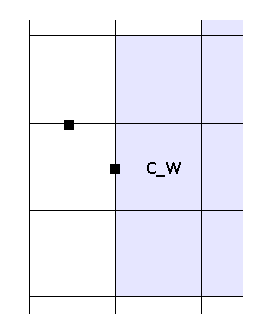
          case GG.C_W:
            {
              U[i - 1][j] = U[i][j];
              V[i - 1][j] = V[i][j];
            } break;

Здесь все аналогично.

клетка с флагом C_NW

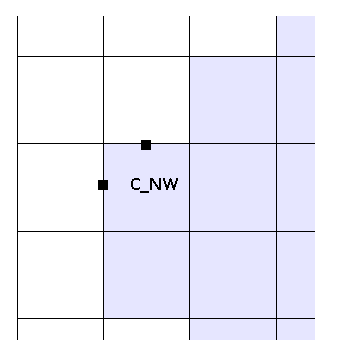
          case GG.C_NW:
            {
              V[i][j] = V[i][j - 1];
              U[i - 1][j] = U[i][j];
            } break;

Здесь значение U в самой клетке будет рассчитано в решателе, т.к. справа от нее есть водная клетка. А вот V нужно проставить, поскольку клетка сверху — пустая.Также необходимо задать значение U[i — 1][j], тк при расчете U[i][j] потребуются значения и в соседних с ней клетках, в том числе и в U[i — 1][j].

Точно также, как и в предыдущем случае значение V[i][j] берем из клетки V[i][j — 1], а не из V[i-1][j] — тк значение в V[i-1][j] может оказаться граничным и еще не известным.

Давление в пустых клетках и клетках поверхности ставим = 0. Это не совсем корректно, но это работает.
В поверхностных клетках давление нужно, потому что при решении уравнения для давления эти клетки являются граничными и в них расчет давления непосредственно не производится.

Алгоритм движения жидкости с помощью частиц только на поверхности

В исходниках присутствуют варианты с именем track в названии. Это метод перемещения свободной поверхности, в котором перемещаются частицы только на самой поверхности, а не во всем объеме жидкости. Это в некоторой степени похоже на метод VOF — но там делается предварительная реконструкция поверхности, что достаточно громоздко. В моем методе если частица ушла из клетки то она помечается пустой, а в находящиеся рядом клетки жидкости в которых нет частиц — добавляются частицы, чтобы знать где находится поверхность. Если же частица переходить в пустую клетку — то клетка помечается как жидкость. Конечно у данного метода есть приличная доля неточности, но зато он быстрый и не требует сложного кодирования.

Implicit схема расчета

В исходниках есть также implicit версия решателя — применяется к уравнениям для скоростей, отличия в коде от explicit версии там минимальные. При дискретизации просто все термы с U и V[i][j] переходят в левую часть уравнения а не в правую как в explicit.Implicit (неявная) схема позволяет делать значительно большие шаги по времени, что в случае с explicit невозможно.
Про implicit можно почитать тут http://math.mit.edu/cse/codes/mit18086_navierstokes.pdf.

3D версия

В 3D версии сделано все по аналогии с 2D.
Управление клавишами F1-F8 + WASD, стрелки и E R PgUp PgDown для поворота камеры.
Для сцен с источником воды — клавиша P — для включения отключения напора воды.
G — получше рендеринг поверхности (вместо кубов используются сферы), но жутко тормозит.
В папке Demos — находятся сцены и параметры (размеры, шаг по времени, гравитация и кол-во частиц на клетку) в виде xml файла. Также есть возможность нарисовать в paint свой HeightMap (карту высот), размеры могут быть любые — есть autoresize.

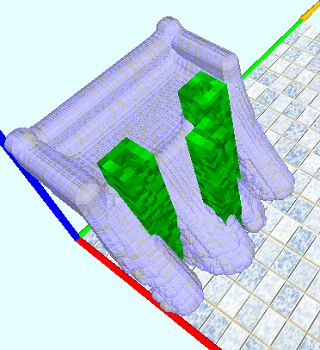
В заключение приведу скрины из 2D и 3D:

Остальные скрины тут

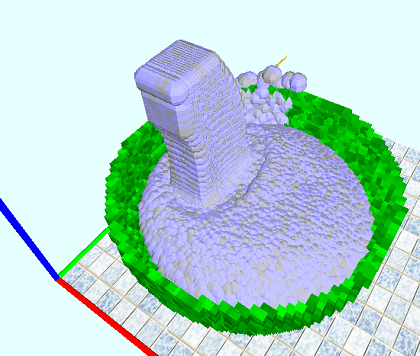
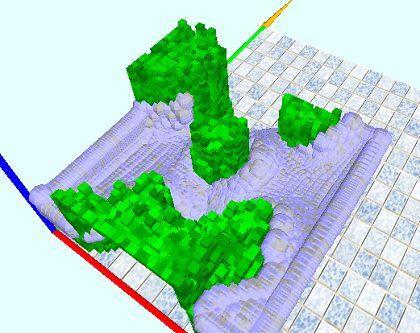
Исходники лежат тут sourceforge.

P.S. Если есть люди, знакомые с CFD, было бы интересно вместе улучшить данный проект в плане скорости и корректности решения (особенно при моделировании поверхности).
Рендеринг я и сам смогу запилить более — менее, а вот математика и физика — это не основное мое направление. Буду рад любым замечаниям и полезным советам.

Автор: scifix

Источник