Введение
Сегодня уже все, кто хоть немного интересуется дата майнингом, наверняка слышали про простую линейную регрессию. Про нее уже писали на хабре, а также подробно рассказывал Эндрю Нг в своем известном курсе машинного обучения. Линейная регрессия является одним из базовых и самых простых методов машинного обучения, однако очень редко упоминаются методы оценки качества построенной модели. В этой статье я постараюсь немного исправить это досадное упущение на примере разбора результатов функции summary.lm() в языке R. При этом я постараюсь предоставить необходимые формулы, таким образом все вычисления можно легко запрограммировать на любом другом языке. Эта статья предназначена для тех, кто слышал о том, что можно строить линейную регрессию, но не сталкивался со статистическими процедурами для оценки ее качества.
Модель линейной регрессии
Итак, пусть есть несколько независимых случайных величин X1, X2, ..., Xn (предикторов) и зависящая от них величина Y (предполагается, что все необходимые преобразования предикторов уже сделаны). Более того, мы предполагаем, что зависимость линейная, а ошибки рапределены нормально, то есть
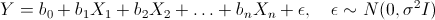
где I — единичная квадратная матрица размера n x n.
Итак, у нас есть данные, состоящие из k наблюдений величин Y и Xi и мы хотим оценить коэффициенты. Стандартным методом для нахождения оценок коэффициентов является метод наименьших квадратов. И аналитическое решение, которое можно получить, применив этот метод, выглядит так:
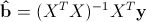
где b с крышкой — оценка вектора коэффициентов, y — вектор значений зависимой величины, а X — матрица размера k x n+1 (n — количество предикторов, k — количество наблюдений), у которой первый столбец состоит из единиц, второй — значения первого предиктора, третий — второго и так далее, а строки соответствуют имеющимся наблюдениям.
Функция summary.lm() и оценка получившихся результатов
Теперь рассмотрим пример построения модели линейной регрессии в языке R:
> library(faraway)
> lm1<-lm(Species~Area+Elevation+Nearest+Scruz+Adjacent, data=gala)
> summary(lm1)
Call:
lm(formula = Species ~ Area + Elevation + Nearest + Scruz + Adjacent,
data = gala)
Residuals:
Min 1Q Median 3Q Max
-111.679 -34.898 -7.862 33.460 182.584
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 7.068221 19.154198 0.369 0.715351
Area -0.023938 0.022422 -1.068 0.296318
Elevation 0.319465 0.053663 5.953 3.82e-06 ***
Nearest 0.009144 1.054136 0.009 0.993151
Scruz -0.240524 0.215402 -1.117 0.275208
Adjacent -0.074805 0.017700 -4.226 0.000297 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 60.98 on 24 degrees of freedom
Multiple R-squared: 0.7658, Adjusted R-squared: 0.7171
F-statistic: 15.7 on 5 and 24 DF, p-value: 6.838e-07
Таблица gala содержит некоторые данные о 30 Галапагосских островах. Мы будем рассматривать модель, где Species — количество разных видов растений на острове линейно зависит от нескольких других переменных.
Рассмотрим вывод функции summary.lm().
Сначала идет строка, которая напоминает, как строилась модель.
Затем идет информация о распределении остатков: минимум, первая квартиль, медиана, третья квартиль, максимум. В этом месте было бы полезно не только посмотреть на некоторые квантили остатков, но и проверить их на нормальность, например тестом Шапиро-Уилка.
Далее — самое интересное — информация о коэффициентах. Здесь потребуется немного теории.
Сначала выпишем следующий результат:
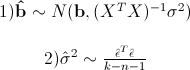
при этом сигма в квадрате с крышкой является несмещенной оценкой для реальной сигмы в квадрате. Здесь b — реальный вектор коэффициентов, а эпсилон с крышкой — вектор остатков, если в качестве коэффициентов взять оценки, полученные методом наименьших квадратов. То есть при предположении, что ошибки распределены нормально, вектор коэффициентов тоже будет распределен нормально вокруг реального значения, а его дисперсию можно несмещенно оценить. Это значит, что можно проверять гипотезу на равенство коэффициентов нулю, а следовательно проверять значимость предикторов, то есть действительно ли величина Xi сильно влияет на качество построенной модели.
Для проверки этой гипотезы нам понадобится следующая статистика, имеющая распределение Стьюдента в том случае, если реальное значение коэффициента bi равно 0:
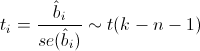
где
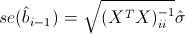— стандартная ошибка оценки коэффициента, а t(k-n-1) — распределение Стьюдента с k-n-1 степенями свободы.
Теперь все готово для продолжения разбора вывода функции summary.lm().
Итак, далее идут оценки коэффициентов, полученные методом наименьших квадратов, их стандартные ошибки, значения t-статистики и p-значения для нее. Обычно p-значение сравнивается с каким-нибудь достаточно малым заранее выбранным порогом, например 0.05 или 0.01. И если значение p-статистики оказывается меньше порога, то гипотеза отвергается, если же больше, ничего конкретного, к сожалению, сказать нельзя. Напомню, что в данном случае, так как распределение Стьюдента симметричное относительно 0, то p-значение будет равно 1-F(|t|)+F(-|t|), где F — функция распределения Стьюдента с k-n-1 степенями свободы. Также, R любезно обозначает звездочками значимые коэффициенты, для которых p-значение достаточно мало. То есть, те коэффициенты, которые с очень малой вероятностью равны 0. В строке Signif. codes как раз содержится расшифровка звездочек: если их три, то p-значение от 0 до 0.001, если две, то оно от 0.001 до 0.01 и так далее. Если никаких значков нет, то р-значение больше 0.1.
В нашем примере можно с большой уверенностью сказать, что предикторы Elevation и Adjacent действительно с большой вероятностью влияют на величину Species, а вот про остальные предикторы ничего определенного сказать нельзя. Обычно, в таких случаях предикторы убирают по одному и смотрят, насколько изменяются другие показатели модели, например BIC или Adjusted R-squared, который будет разобран далее.
Значение Residual standart error соответствует просто оценке сигмы с крышкой, а степени свободы вычисляются как k-n-1.
А теперь самая важные статистики, на которые в первую очередь стоит смотреть: R-squared и Adjusted R-squared:
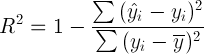
где Yi — реальные значения Y в каждом наблюдении, Yi с крышкой — значения, предсказанные моделью, Y с чертой — среднее по всем реальным значениям Yi.
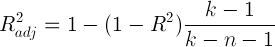
Начнем со статистики R-квадрат или, как ее иногда называют, коэффициента детерминации. Она показывает, насколько условная дисперсия модели отличается от дисперсии реальных значений Y. Если этот коэффициент близок к 1, то условная дисперсия модели достаточно мала и весьма вероятно, что модель неплохо описывает данные. Если же коэффициент R-квадрат сильно меньше, например, меньше 0.5, то, с большой долей уверенности модель не отражает реальное положение вещей.
Однако, у статистики R-квадрат есть один серьезный недостаток: при увеличении числа предикторов эта статистика может только возрастать. Поэтому, может показаться, что модель с большим количеством предикторов лучше, чем модель с меньшим, даже если все новые предикторы никак не влияют на зависимую переменную. Тут можно вспомнить про принцип бритвы Оккама. Следуя ему, по возможности, стоит избавляться от лишних предикторов в модели, поскольку она становится более простой и понятной. Для этих целей была придумана статистика скорректированный R-квадрат. Она представляет собой обычный R-квадрат, но со штрафом за большое количество предикторов. Основная идея: если новые независимые переменные дают большой вклад в качество модели, значение этой статистики растет, если нет — то наоборот уменьшается.
Для примера рассмотрим ту же модель, что и раньше, но теперь вместо пяти предикторов оставим два:
> lm2<-lm(Species~Elevation+Adjacent, data=gala)
> summary(lm2)
Call:
lm(formula = Species ~ Elevation + Adjacent, data = gala)
Residuals:
Min 1Q Median 3Q Max
-103.41 -34.33 -11.43 22.57 203.65
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 1.43287 15.02469 0.095 0.924727
Elevation 0.27657 0.03176 8.707 2.53e-09 ***
Adjacent -0.06889 0.01549 -4.447 0.000134 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 60.86 on 27 degrees of freedom
Multiple R-squared: 0.7376, Adjusted R-squared: 0.7181
F-statistic: 37.94 on 2 and 27 DF, p-value: 1.434e-08
Как можно увидеть, значение статистики R-квадрат снизилось, однако значение скорректированного R-квадрат даже немного возросло.
Теперь проверим гипотезу о равенстве нулю всех коэффициентов при предикторах. То есть, гипотезу о том, зависит ли вообще величина Y от величин Xi линейно. Для этого можно использовать следующую статистику, которая, если гипотеза о равенстве нулю всех коэффициентов верна, имеет распределение Фишера c n и k-n-1 степенями свободы:
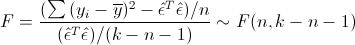
Значение F-статистики и p-значение для нее находятся в последней строке вывода функции summary.lm().
Заключение
В этой статье были описаны стандартные методы оценки значимости коэффициентов и некоторые критерии оценки качества построенной линейной модели. К сожалению, я не касался вопроса рассмотрения распределения остатков и проверки его на нормальность, поскольку это увеличило бы статью еще вдвое, хотя это и достаточно важный элемент проверки адекватности модели.
Очень надеюсь что мне удалось немного расширить стандартное представление о линейной регрессии, как об алгоритме который просто оценивает некоторый вид зависимости, и показать, как можно оценить его результаты.
Автор: DeMoerto
