
Я обнаружил этот фрактал, когда разглядывал интерференцию волн на поверхности речки. Волна движется к берегу, отражается и накладывается сама на себя. Есть ли порядок в тех узорах, которые создаются волнами? Попробуем найти его. Рассмотрим не всю волну, а только вектор ее движения. «Берега» сделаем гладкими, для простоты эксперимента.
Эксперимент можно провести на обычном листке в клеточку из школьной тетради.
Или используя JavaScript реализацию алгоритма.
Английская версия: New kind of fractals — Fractals in relatively prime integers (coprime integers)
Возьмем прямоугольник со сторонами q и p. Отправим луч (вектор) из угла в угол. Луч двигается к одной из сторон прямоугольника, отражается и продолжает движение к следующей стороне. Это продолжается до тех пор, пока луч не попадет в один из оставшихся углов. Если размер стороны q и p — взаимно просты числа, то получается узор (как мы увидим позже — фрактал).
На картинке мы ясно видим, как работает этот алгоритм.
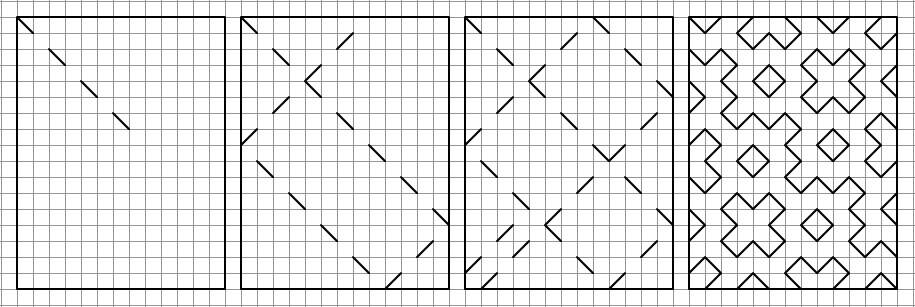
Gif-анимация:


Самое удивительное то, что с разными сторонами прямоугольника — получаем разные узоры.












Почему я называю эти узоры фракталами? Как известно, «фрактал» — это геометрическая фигура, обладающая свойствами самоподобия. Часть картинки повторяет всю картинку в целом. Если значительно увеличить размеры сторон Q и P — ясно, что эти узоры обладают свойствами самоподобия.
Попробуем увеличить. Увеличивать будем хитрым способом. Возьмем, например, узор 17x29. Следующие узоры будут: 29x(17+29=46), 46x(29+46=75)…
Одна сторона: F(n);
Вторая сторона: F(n+1)=F(n)+F(n-1);
17, 29, 46, 75, 121, 196, 317, 513, 830, 1343
Как числа Фибоначчи, только с другими первым и вторым членом последовательности: F(0)=17, F(1)=29.









Дальше фракталы циклически повторяются.
Если большая сторона четная, получается такой узор:

Если меньшая сторона четная:

Если обе стороны нечетные — получаем симметрический узор:


В зависимости от того, как начинается луч:

или

Попробую объяснить, что происходит в этих прямоугольниках.
Отделим от прямоугольника квадрат, и посмотрим, что происходит на границе.
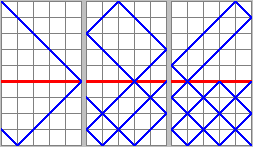
Луч выходит в той-же точке, откуда зашел.
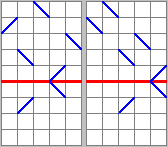
При этом, количество квадратиков, которые проходит луч — всегда четное число.
Поэтому, если отрезать от прямоугольника квадрат — останется не измененная часть фрактала.
Если отделять от фрактала квадраты столько раз, сколько это возможно — можно добраться до «начала» фрактала.
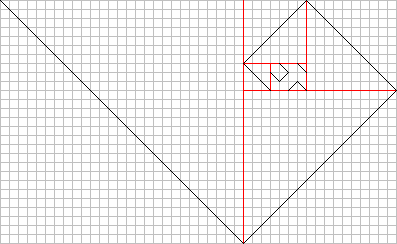
Похоже на спираль Фибоначчи?
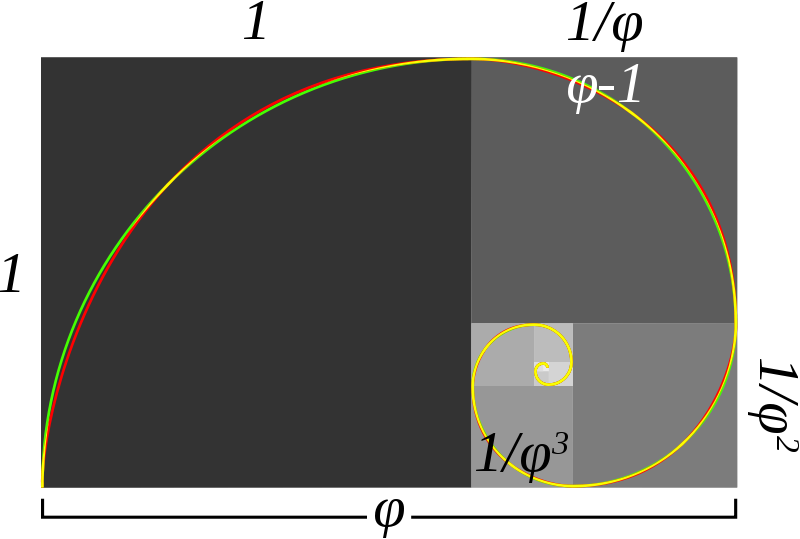
Из чисел Фибоначчи тоже можно получить фракталы.
В математике числами Фибоначчи (ряд Фибоначчи, последовательность Фибоначчи) называют числа:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597…
По определению, первые две цифры в последовательности Фибоначчи 0 и 1, а каждое последующее число равно сумме двух предыдущих.
F(n)=F(n-1)+F(n-2)
F(0)=0, F(1)=1
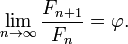
Поехали:
Как мы видим, чем ближе отношение сторон приближается к золотому сечению — тем больше детализация фрактала.

При этом фрактал повторяет часть фрактала, увеличенного на 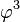 .
.
Вместо чисел Фибоначчи можно использовать иррациональные размеры сторон:
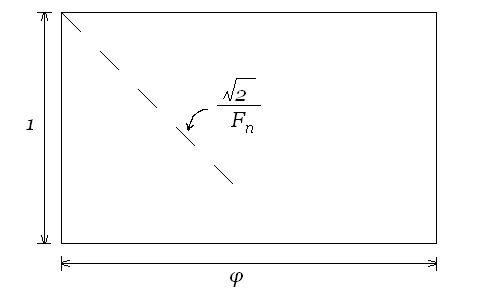
Получим тот-же фрактал.
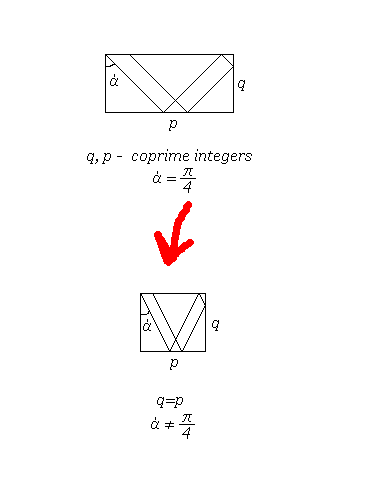
Те-же фракталы можно получить и в квадрате, если пускать луч под другим углом:
Что можно сказать в заключении?
Хаос — это тоже порядок. Со своими закономерностями. Порядок этот не изученный, но вполне поддающийся изучению. А все стремление науки — обнаружить эти закономерности. И в конечном итоге соединить детали головоломки, чтобы увидеть общую картину.
Давайте посмотрим на поверхность речки. Если бросить в нее камень — пойдут волны. Круги, вполне поддающиеся изучению. Скорость, период, длину волны — все это можно подсчитать. Но до тех пор, пока волна не дойдет до берега, не отразиться и не начнет накладываться на саму себя. Получим хаос (интерференцию), который уже трудно поддается изучению.
Что если двигаться от обратного? Упростить поведение волны на столько, на сколько это возможно. Упростить, найти закономерность и после этого попробовать описать уже полную картину происходящего.
Что можно упростить? Очевидно, что сделать отражающую поверхность прямой, без изгибов. Далее, вместо самой волны, использовать только вектор движения волны. В принципе, этого достаточно, чтобы построить простой алгоритм и смоделировать процесс на компьютере. И даже вполне достаточно, чтобы сделать «модель» поведения волны на обычном листке в клеточку.
Что имеем в результате? В результате видим, что в волновых процессах (та-же рябь на поверхности речки) имеем не хаос, а наложение фракталов (самоподобных структур) друг на друга.
Рассмотрим другой вид волн. Как известно, электромагнитная волна состоит из трех векторов — волновой вектор и вектора напряженности электрического и магнитного поля. Как видим, если «словить» такую волну в замкнутой области – там, где пересекаются эти вектора, получаем вполне четкие замкнутые структуры. Быть может, элементарные частицы – это такие-же фракталы?

Все фрактальчики в прямоугольниках от 1 до 80 (6723х6723 px):

Замкнутые области во фракталах (6723х6723 px):


Просто красивый фрактал (4078x2518 px):

Если у вас хватило терпения дочитать до конца, еще раз JavaScript реализация алгоритма :)
Автор: xcont













