Винтик и Шпунтик — Сhallenge продолжается

2025-03-24 в 14:32, admin, рубрики: математика, олимпиадное программирование, теория групп

Некоторое время назад я объявил челлендж имени Винтика и Шпунтика. Суть его — в подсчете числа решений задачки, почерпнутой из математической олимпиады для 7 класса. Изначально я рассчитывал на то, что лучшие умы Хабра разберутся с задачей за месяц. Однако с тех пор прошло 10, и не сказать, чтобы обозначились какие-то серьезные прорывы. Но некоторые новые идеи появились. Поэтому сегодня мы подведем промежуточные итоги нашего челленджа, а также разберем некоторые подходы, которые позволяют двигаться вперед в нашем нелегком деле.

Для начала снова приведу условия задачи.

«Незнайка записывает 9 разрядов 10-значного десятичного числа и пропускает один по своему выбору. Пропущенный разряд он предлагает записать Винтику, а затем показывает полученное 10 -значное число Шпунтику. Как могут Винтик и Шпунтик договориться, чтобы Шпунтик угадал, какой именно разряд записал Винтик?»

Ну, то есть Незнайка может написать что-то такое: 01234...6789 (ведущие нули допускаются). Или такое: 000111...223. Или вообще вот такое: ...777777777. Винтик дописывает одну недостающую цифру (пусть в первом случае это будет 5). Затем Незнайка показывает полученное число 0123456789 Шпунтику. И тот должен угадать, что именно пятый разряд Незнайка пропустил, а Винтик, соответственно, записал.

Итак, вопрос, на который предстоит найти ответ.

Сколько есть взаимно‑однозначных отображений между множествами 10⁹(записанные Незнайкой разряды)*10(номер пропущенного) и 10¹⁰ (десятизначное число, которое видит Шпунтик)?

Сразу скажу, что десятичный (десятизначный) случай пока представляется практически неподъемной проблемой. Чуть забегая вперед, замечу, что пространство вариантов перебора растет как $X^{{X}^{X}}$ . А $10^{{10}^{10}}$ — это даже для суперкомпьютера неподъемная тяжесть. Поэтому более продуктивный подход состоит в анализе редуцированных случаев (бинарного, тернарного, кватернарного и тд). Вот с них мы и начнем.

Бинарный случай

В данном случае записываемые разряды могут принимать значения 0 и 1. И их всего два: один по своему выбору записывает Незнайка, а второй предстоит записать Винтику. Бинарный случай тривиален, я подозреваю, это связано с тем, что S(2) является единственной коммутативной среди всех симметрических групп. Тем не менее, давайте разберем этот случай, чтобы познакомиться с основными подходами.

«Таблицы Шмелева»

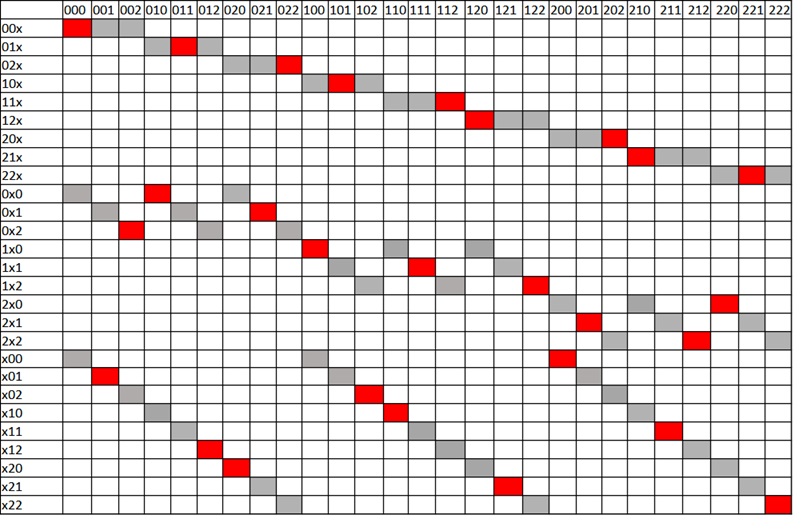
Для начала посмотрим, как выглядит наша задача в графическом представлении. Табличками Шмелева я называю матрицы смежности двудольного графа, ибо именно Алексей Сергеевич Шмелев указал на удобство их использования. В бинарном случае она будет выглядеть вот так.

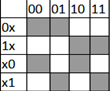
В первом столбце показано то, что видит Винтик (где x обозначает пропущенный разряд). В первой строке то, что видит Шпунтик (двузначное число). Решение должно задавать взаимно однозначное соответствие, то есть у нас должно быть по одному элементу в каждой строке и в каждом столбце. Что приводит нас к задаче расстановки не бьющих друг друга ладей на доске специального вида, где не все клетки доступны (только те, которые выделены серым). В общем случае задача расстановки ладей является NP — трудной. Но у нас случай не общий, а очень даже конкретный, и он допускает только два решения.

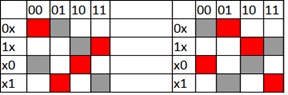
Понижение размерности.

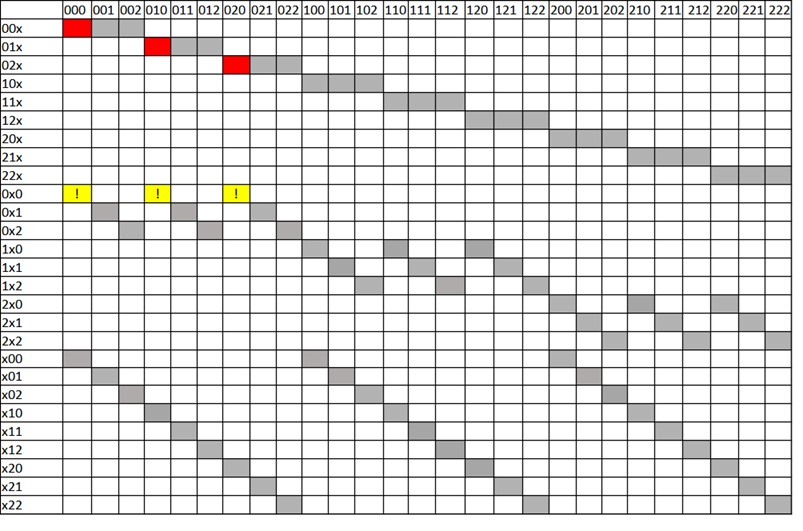
Давайте покажу еще один трюк, который я называю понижением размерности. Как мы увидим в дальнейшем, основную роль в поиске решений будет играть «верхняя линия» матрицы смежности. Это те строки (первая и вторая), которые соответствуют случаю, когда Незнайка пропускает крайний правый разряд. Заметим еще, что в «верхней линии» в обоих решениях есть один элемент, который при делении на 2 (основание) дает в остатке 0, а второй — 1. Как мы увидим далее, это общее свойство задачи Винтика и Шпунтика. Таким образом мы можем свести наш кейс к «задаче о раскрасках» существенно меньшей размерности. Назовем элемент, дающий в остатке от деления на 2 ноль — «красным», а единицу — «синим».

Таким образом, теперь нам надо раскрасить верхнюю диагональ (одномерное многообразие) так, чтобы у нас был один красный и один синий элемент. Сделать это можно всего лишь двумя способами.

Винтик и Шпунтик — Сhallenge продолжается - 5

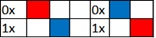
И они будут соответствовать решениям, полученным выше.

Тернарный случай

Тернарный кейс является первым нетривиальным в задаче. Здесь у нас уже три разряда, которые могут принимать значения -0,1,2. «Табличка Шмелева» имеет вид:

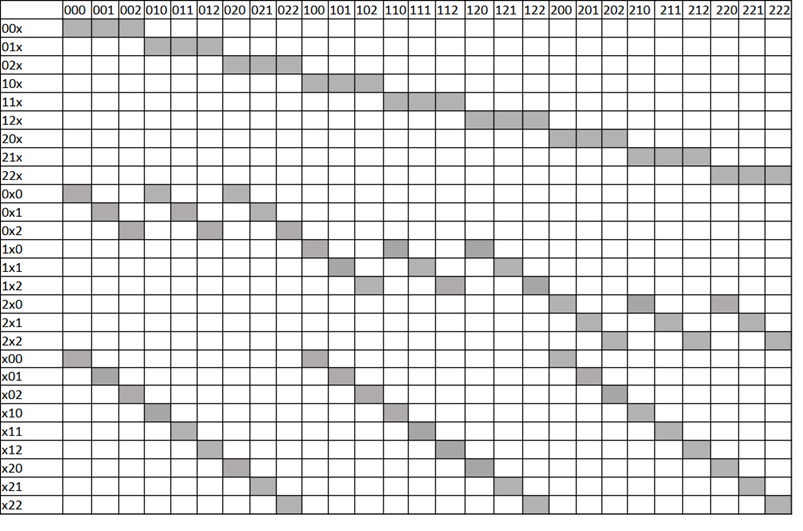
А вот так может выглядеть решение.

Но сколько их всего? Чтобы ответить на этот вопрос, давайте напишем небольшой кусок кода, осуществляющий перебор всех возможных вариантов. Оно рекурсивно спускается с нулевой до 26й строчки и проверяет взаимную однозначность соответствия.

// dummy. cpp

#include <stdio.h>

int col[27]; //массив флагов. флаг = 1, если в столбце уже есть элемент решения и 0 в противном случае

int start[27] = { 0,3,6,9,12,15,18,21,24,0,1,2,9,10,11,18,19,20,0,1,2,3,4,5,6,7,8 };//позиции первых слева элементов в строках матрицы смежности

int inc[27] = { 1,1,1,1,1,1,1,1,1,3,3,3,3,3,3,3,3,3,9,9,9,9,9,9,9,9,9 };//расстояния между элементами в строках

int solutions[10753][27]; // массив решений

int count;//счетчик решений

void line(int level) // итерация по строке

{

    int x, i;

    x = start[level]; // устанавливаем начальную позицию

    for (i = 0; i < 3; i++) //цикл по 3м точкам в строке 

    {

        if (col[x]) // проверяем флаг для текущего столбца

        {

            x += inc[level];

            continue;

        }

        if (level == 26) // для последней строки инкрементируем счетчик решений

        {

            for (i = 0; i < 27; i++) solutions[count + 1][i] = solutions[count][i]; //сохраняем полученное решение

        

            count++;

            break;

        }

        col[x] = 1; // устанавливаем флаг

        line(level + 1); // запускаем поиск для следующей строки

        col[x] = 0; // сбрасываем флаг

        x += inc[level]; //переходим к следующему элементу

    }

}

int main()

{

    for (int i = 0; i < 27; i++) col[i] = 0; //обнуляем флаги

    count = 0;

    line(0);

    printf("%d", count);

    getchar();

}

Даже на моем не самом мощном ноутбуке этот убогий однопоточный перебор отрабатывает за пару секунд. Конечно, его можно оптимизировать. Первое, что приходит в голову — исключать в процессе перебора запрещенные комбинации.

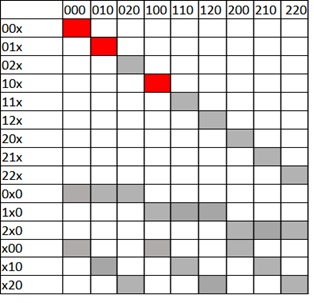
Например,

Мы не можем размещать элементы в первой линии таким образом, ибо «блокируем» целую строчку в линии второй. А это невозможно, ибо отображение наше должно быть 1 в 1. Исключение подобных комбинаций даст нам некоторое ускорение перебора. Но в данном случае — незачем, а в более высоких размерностях это, увы, не помогает. Здесь мы имеем $3^{{3}^{3}}=3^{27}approx10^{13}$ вариантов, и это маленькое число. А вот в четверичном случае пространство перебора $4^{{4}^{4}}=4^{256}approx 10^{153}$ , и это число уже большое (хотя и не бесконечное). Но подход «в лоб» не работает. Приходится что-то придумывать. А уж в пятеричном случае $5^{{5}^{5}}=5^{3125}approx 10^{2184}$ и подавно…

Но давайте вернемся к результату наших вычислений. Мы получили Это выглядит странно. Немного удивляет степень двойки — даже в числе 9! (появления которого можно было бы ожидать) содержится всего 7 двоек. И непонятно, откуда взялась семерка в задаче, где интуитивно больше ожидаешь троек. И тем не менее 10 752 — это правильный ответ. Давайте разбираться, как же он получается.

Вклад двух «нижних линий» и метод «разделения переменных».

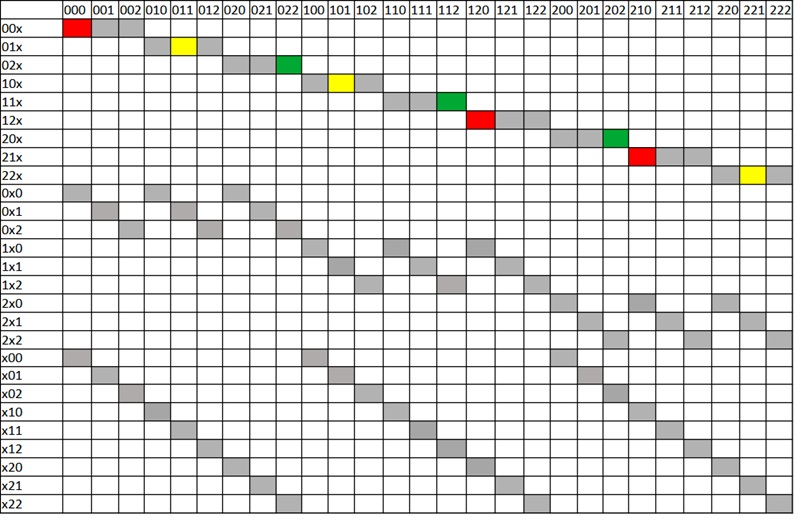
Интересной особенностью задачи про Винтика и Шпунтика является то, что две «нижние линии» (в тернарном случае строки 9–17 и 18–26) дают очень простой вклад. Для заданной конфигурации «верхней линии» (строки 0–8) мы получаем разных решений. Намечу идею доказательства этого факта. Для этого воспользуемся еще одним трюком, который я называю «разделением переменных». Для этого заметим, что в матрице смежности мы имеем по сути три разных «подсетки». В первую входят столбцы и строки, номера которых делятся на 3 нацело, во вторую — с остатком 1, в третью — с остатком 2. Давайте возьмем первую из них.

Номера столбцов и строк делятся на 3 нацело

Мы получили три «подсетки» размером 9×9, которые «интерферируют» друг с другом только на уровне «верхней линии». Но мы договорились, что она у нас определена (например, так, как показано на рисунке). А значит, мы можем анализировать каждое подмножество независимо. И легко показать, что для каждой конфигурации верхней строчки мы будем иметь ровно два решения. В то случае, который я привел на рисунке, всё элементарно сводится к бинарному кейсу, в котором два решения. Но на самом деле все будет так же при любом допустимом выборе трех красных ячеек. Ну а поскольку «подсеток» у нас 3, и они независимы, то мы получаем или 8 решений для каждой конфигурации верхней линии. На самом деле метод «разделения переменных» имеет важное значение для оптимизации решения задачи Винтика и Шпунтика. Как только мы определили конфигурацию верхней линии, мы можем искать число решений для каждой «подсетки» независимо от других. А результат будет просто их произведением.

Ну и, забегая вперед, скажу, что вклад двух «нижних линий» всегда будет степенью двойки. Он дает множитель $2^{n^{n-2}}$ , где n — это размерность кейса.

Итак, мы определили ключевую роль «верхней линии» и даже знаем, сколько существует вариантов решений . Осталось понять, как это число получается. Пару лет назад я нашел чисто комбинаторное решение, которое основано на подсчете «запрещенных комбинаций». Идея в том, чтобы взять полное число размещений и исключить невозможные. Но это решение мне не нравится, поскольку непонятно, как обобщить его на более высокие размерности. Поэтому сейчас мы воспользуемся уже известным методом.

Понижение размерности и «раскраска квадрата».

Так же, как и раньше, нам нужно разместить в «верхней линии» матрицы смежности 9 элементов. Горизонтальные координаты трех из них при делении на 3 дают в остатке 0 — назовем их «красными». Те, которые дают в остатке 1, назовем «желтыми». 2 — «зелеными».

А теперь давайте назовем первые три элемента верхней строкой квадрата 3×3. Следующие три — второй, а последние — третьей.

Итак, мы свели задачу в тернарном случае к раскраске квадрата (двумерного многообразия) в три цвета (по три элемента в каждый). При этом у нас не может быть трех ячеек одного цвета в одной строке или одном столбце. Это будут «запрещенные комбинации», блокирующие вторую или третью линии в оригинальной матрице. Эту задачу (чем‑то напоминающую кубик Рубика) я уже приводил на Хабре. Несмотря на кажущуюся простоту постановки, в ней масса интересных тонкостей.

Начнем с того, что общее количество размещений трех красных, трех желтых и трех зеленых ячеек на 9 клеточках . Для перебора это число мизерное. И все же (вспоминая о более высоких размерностях) хочется его как-то «уменьшить». Для этого заметим, что задача наша обладает определенным набором симметрий. Перестановка строк в квадрате (эта группа изоморфна S(3)) переводит решение в решение. То же самое с перестановкой столбцов (тоже S(3)). Также «перекрашивание» (красные в желтые, желтые в зеленые и тп) дает еще одно S(3). Ну и наконец транспонирование матрицы или поворот на также переводит решение в решение. Тут стоит оговориться о том, что транспонирование не коммутирует с перестановками. Однако ситуацию спасает то, что транспонирование с последующей перестановкой строк эквивалентно перестановке столбцов с последующим транспонированием.

Всего в нашей группе будет элемента. Мы хотим подсчитать, сколько существует орбит у этой группы симметрий, ибо очевидно, что число орбит будет сильно меньше, чем число решений. Это можно сделать по лемме Бернсайда, последовательно применяя элементы группы к каждой из 1680 перестановок. Это значительное количество вычислений, которых можно избежать. Для этого мы воспользуемся теоремой Пойа, а затем ее обобщением, предложенным Де Брейном.

Теорема Редфилда-Пойа и «структура дефектов»

Сначала запишем цикловой индекс «геометрической части» нашей группы (перестановки строк, столбцов и транспонирование)

$G(t)=frac1{72}(t_1^9+12t_1^3t_2^3+9t_1t_2^4+18t_1t_4^2+8t_3^3+24t_3t_6)$

Теперь давайте воспользуемся теоремой Пойа, чтобы посчитать, сколько существует «топологически» разных (не переходящих друг в друга преобразованиях группы) способов разместить три красных ячейки в квадрате 3 на 3. Придадим красному вес x, а остальному — 0,

$G(x)=frac1{72}((x+1)^9+12(x+1)^3(x^2+1)^3+9(x+1)(x^2+1)^4+\18(x+1)(x^4+1)^2+8(x^3+1)^3+24(x^3+1)(x^6+1))$

и вычислим коэффициент при x3 (три ячейки). Получается 288. Следовательно, у нас всего 288/72 = 4 типа или, как я их называю, «дефекта». Давайте их изобразим:

Винтик и Шпунтик — Сhallenge продолжается - 25

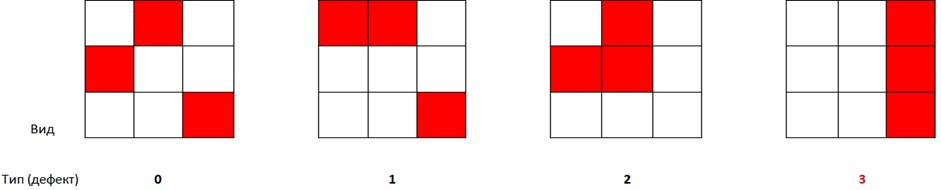
Первую (слева) расстановку отнесем к типу 0, поскольку все красные ячейки находятся в разных столбцах и строках. Во второй у нас есть строчный «дефект» — две красных ячейки в верхней строке. Это тип 1. В третьей есть и строчный, и столбцовый «дефекты» — это тип 2. Ну и в 4 три красных ячейки расположены в одном столбце. Это тип 3 (запрещенная комбинация). Очевидно, что точно такие же типы будут и для двух других цветов, поскольку задача обладает цветовой симметрией. Так что мы можем сделать обобщение. Например, вот такую расстановку

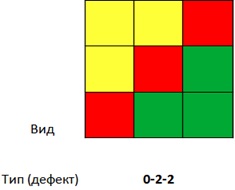
назовем «структурой дефектов» 0–2–2. Красные ячейки не дают «дефектов», а желтые и зеленые имеют и строчные, и столбцовые. Легко убедиться, что «геометрические» преобразования (перестановки строк, столбцов, и транспонирование) не изменяют структуру дефектов, а «перекрашивания» просто меняют цифры местами. Для общности мы можем ввести какую‑нибудь симметричную суперпозицию F(R,Y,G), где R — дефект красных ячеек, Y и G — желтых и зеленых соответственно. И значение этой функции будет сохраняться при преобразованиях группы. Но мы пока не будем определять явный вид этой функции.

Теорема де Брейна и полное число орбит.

Сейчас мы хотим сосчитать, сколько существует различных «структур дефектов» для трех цветов. Мы, как и раньше, можем воспользоваться для этого теоремой Пойа. Придадим красным ячейкам вес x, желтым — у, зеленым — z. И подставим это в цикловой индекс G(t). Для того, чтобы подсчитать количество раскрасок в три цвета, нам нужен коэффициент при xyz (по три ячейки каждого цвета). Он равен 2160, и мы получаем орбит. Это все еще довольно большое число. Дело в том, что теорема Пойа учитывает только пространственную симметрию и не учитывает симметрию цветовую. Мы можем отождествить решения, полученные перекрашиванием красных ячеек в желтые, а желтых — в красные. Или красных в зеленые, зеленых в желтые, а желтых в красные. С тем, как учесть эту цветовую симметрию, я довольно долго возился, и, ничего не придумав, пошел за советом к Саше Гасникову. Но он, как всегда, был очень занят, и перенаправил меня к Диме Ильинскому. И вот Дима указал мне на замечательное обобщение теоремы Пойа, предложенное Де Брейном и позволяющее учесть «перекрашивания» при подсчете числа орбит. Для того чтобы им воспользоваться, запишем цикловой индекс «группы перекрашиваний». Напомню, что цикловой индекс группы перестановок трех элементов S(3) равен

$S(t)=frac1{6}(t_1^3+3t_1t_2+2t_3)$

Поскольку у нас по три элемента каждого цвета, рука сама тянется написать

$C(t)=frac1{6}(t_1^9+3t_1^3t_2^3+2t_3^3)$

Но, увы, это неверно. Дело обстоит сложнее, поскольку ячейки могут отображаться на свой цвет. И все же по аналогии с предыдущей формулой мы будем искать ответ в виде

Где С₁ — это слагаемое, отвечающее за перестановки ячеек внутри одного цвета. И оно равно произведению цикловых индексов

С₂ отвечает за ситуацию, когда ячейки одного цвета (например красного) остаются на месте, а два других (зеленые и желтые) переходят друг в друга.

А С₃ за циклическую перестановку всех трех цветов.

Как мы видим, индекс «группы перекрашиваний» «наследует» структуру индекса группы перестановок трех элементов с точностью до длины циклов и числовых множителей (желающие проверить могут поупражняться в комбинаторике). Окончательно получим

$C(t)=t_1^9+9t_1^7t_2+6t_1^6t_3+27t_1^5t_2^2+12t_1^3t_3^2+45t_1^3t_2^3+\36t_1^4t_2t_3+54t_1^2t_2^2t_3+36t_1t_2t_3^2+80t_3^3+54t_1t_2^4+36t_2^3t_3+\54t_1^3t_2t_4+36t_1^3t_6+162t_1t_2^2t_4+108t_1t_2t_6+108t_2t_3t_4+288t_3t_6+144t_9$

А теперь воспользуемся теоремой Де Брейна. Она является обобщением теоремы Пойа для случая, когда помимо геометрической группы перестановок действует еще и «группа перекрашиваний». Формула де Брейна представляет один из индексов в виде многочлена от операторов дифференцирования и утверждает, что число орбит будет равно следующему выражению:

$G(fracpartial{partial t_1},fracpartial{partial t_2},fracpartial{partial t_3},...)C(t_1,2t_2,3t_3,...)$

При

Осуществив все необходимые дифференцирования и арифметические вычисления, получим для нашего случая 10 орбит. Они будут выглядеть вот так:

Итак, у нас 7 разрешенных орбит и 3 запрещенных. Суммарная длина разрешенных — 1344, запрещенных — 336. Итого 1344+336 =1680, как и должно быть. Но сильно радоваться еще рано. Дело в том, что типы орбит и их длины я получил, применяя групповую классификацию к решениям, найденным в результате перебора. Однако, если мы хотим какого‑то ускорения, действовать надо по‑другому.

Задача «перечисления» и длины орбит

Мы знаем, что орбит у нас всего 10. Было бы здорово придумать какой-то регулярный алгоритм, который выдает по одному представителю каждой орбиты. Это я называю задачей «перечисления». Ну, например, начать с 4 типов орбит для ячеек одного цвета и поочередно добавлять к ним типы орбит второго. Это всего лишь 4×4 варианта и в тернарном случае задачка решается в уме. Но вот при более высоких размерностях она становится нетривиальной, и ее решение еще только предстоит найти. После того как мы перечислим все типы орбит (возьмем по одному представителю от каждого), нам надо узнать их длины. Это уже попроще: мы берем представителя каждой орбиты и по очереди применяем к нему все 432 элемента нашей группы преобразований. Далее мы просто будем записывать уникальные решения, если перед нами стоит задача построения всего множества решений. А если нам нужно только их число, можно просто подсчитать количество «cтабилизаторов» — элементов группы, которые переводят данную расстановку в себя. А затем найти длину орбиты данного элемента, пользуясь теоремой Лагранжа. Для этого надо поделить полное количество элементов группы (432) на количество «стабилизаторов» данного элемента. Вы можете спросить: какая разница между приведенным в самом начале «тупым алгоритмом» и этим, если мы все равно занимаемся перебором? Да, но, во‑первых, сейчас мы перебираем элементы группы, а их совсем немного (432 против 3 в 27). А во‑вторых, здесь мы имеем дело с регулярной процедурой, которая на каждом шагу выдает нам решение. И мы можем оценить ее трудоемкость. Однако совсем здорово было бы ничего не считать, а сразу сказать по виду представителя орбиты, сколько у него стабилизаторов в нашей группе симметрий. Увы, как это сделать, мне тоже неизвестно. Так что даже в тернарном случае задаче Винтика и Шпунтика еще хватает «белых пятен».

Еще немного симметрии

Обращу внимание на одну интересную деталь. Несмотря на то, что «пространство дефектов» трехмерно (R,Y,G), два индекса у нас всегда повторяются (чего и следовало ожидать, ибо задача симметрична). Мы можем «cвернуть пространство» в плоскость. Ну например, тип 0–0–0 обозначим 0–0*, 2–1–1 — 21* и тп. Первым идет «непарный» индекс ‑x, а вторым — парный — y*. Давайте сведем в этих обозначениях длины орбит в следующую (двумерную!) таблицу.

Винтик и Шпунтик — Сhallenge продолжается - 38

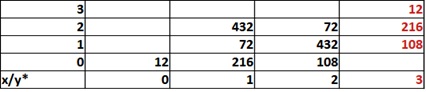
Мы замечаем, что наша таблица симметрична относительно главной диагонали. Более того, мы можем сказать, что 0 в определенном смысле «дуален» 3, а 1 – 2. Ну то есть орбита типа 00* имеет такую же длину, как 33*, 12* такую же, как 21* и тд. Это наталкивает на мысль о том, что существуют преобразования, переводящие одно в другое. При поиске этих преобразований я руководствовался двумя гипотезами.

1. Они должны иметь чисто геометрическую природу, никак на связанную с перекрашиваниями.

2. Их должно быть два, и их комбинация должна давать транспонирование.

Таких преобразований можно написать несколько, приведу самые простые, на мой взгляд.

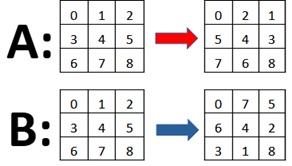
Легко проверить, что . Эти преобразования действительно переводят дуальные орбиты друг в друга. Например,

Винтик и Шпунтик — Сhallenge продолжается - 41

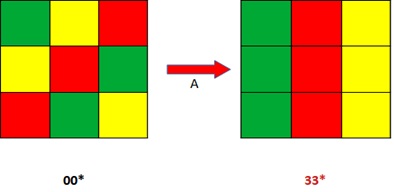
Или

Винтик и Шпунтик — Сhallenge продолжается - 42

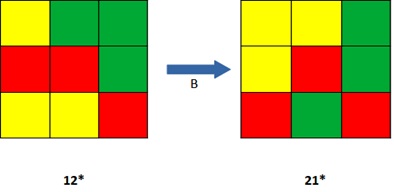
То есть, если мы заменим в нашей группе симметрий транспонирование на преобразования A и B, то вместо 10 орбит получим всего 4. (Можно было бы опять выписать цикловые индексы и воспользоваться теоремой де Брейна. Но мы сейчас этого делать не будем, оставим в качестве домашнего задания )

Тип 0: 00*,33*

Тип 1: 01*,02*,31*,32*

Тип 2: 11*, 22*

Тип 3: 12*, 21*

C четырьмя орбитами, конечно, легче иметь дело, чем с десятью с точки зрения «перечисления». C другой стороны, здесь мы не имеем такой простой интерпретации, как в случае транспонирования. Напрашивается аналогия с квантовой теорией поля, где существуют симметрии, «смешивающие» состояния материи (например бозонное и фермионное). Вот так и у нас: преобразования А и B «смешивают» разрешенные и запрещенные комбинации. Однако то, что орбит получается всего 4 (2х2) вселяет надежду, что в основе всей конструкции лежит какой-то более простой объект. Но об этом (как и о многом другом) еще только предстоит подумать.

Кватернарный (четверичный) случай

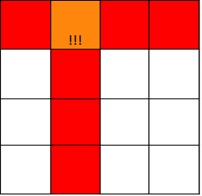
О нем мне пока известно очень мало. Ограничусь лишь наброском схемы решения и грубыми оценками их числа. Укажу на несколько отличий четверичного случая от тернарного. Ну, во‑первых, размер матрицы смежности — 256×256, что делает «тупой перебор» практически бесполезным. Во‑вторых, если раньше у нас был только вклад «верхней» и «двух нижних линий»(степень двойки), то сейчас у нас возникнет «вторая линия». И ее вклад в количество решений будет зависеть от типа расстановки в линии «верхней». Третье отличие связано с новым типом блокировок. Помимо простого случая, когда 4 ячейки в верхней линии блокируют одну из нижних, здесь у нас возникает вот такой случай. (Сразу оговорюсь, что для кватернарного случая я воспользуюсь методом «разделения переменных» — возьму ту четверть, координаты которой делятся на 4 без остатка. Ибо смотреть на табличку 64×64 еще как-то можно, а 256×256 уже нет )

Подобная расстановка красных ячеек в верхней строке является невозможной, ибо здесь мы сталкиваемся с неразрешимым выбором. В четвертом столбце у нас есть две оранжевые ячейки. Это означает, что все остальные элементы в соответствующих строках «заблокированы» элементами верхней линии. Но какую бы из этих ячеек мы ни выбрали, это приведет к нарушению взаимной однозначности отображения. И наличие этого нового типа блокировок сильно осложняет (и без того нелегкую) жизнь переборным алгоритмам. Вместо этого мы пойдем путем, аналогичным тернарному случаю.

«Понижение размерности» и «раскраска» куба.

Давайте «раскрасим» верхнюю линию так, как мы это делали в случае размерности три. Всего у нас будет 64 ячейки 4 цветов (красные, желтые, зеленые, синие). По 16 каждого цвета. Легко сообразить, что эти ячейки мы можем расположить в виде кубика (трехмерное многообразие!) 4x4x4. При этом «запрещенными» у нас будут не только комбинации «четыре в ряд», но новые. Вот такого типа:

Винтик и Шпунтик — Сhallenge продолжается - 44

Это проекция на плоскость одного из сечений нашего куба. Она соответствует случаю, описанному выше.

Теперь выпишем цикловой индекс «геометрической группы перестановок». Она состоит из перестановок «слоев» куба (4×4 = 16 кубиков, лежащих в одной плоскости, параллельной одной из граней) вдоль осей x,y, z. Перестановка вдоль каждой оси изоморфна S(4). Также решение в решение переводят три транспонирования куба относительно плоскостей проходящих через противоположные ребра и два поворота на 120% относительно осей проходящих через противоположные вершины (эта группа изоморфна S(3)). Всего в нашей группе будет элемента.

В итоге получаем:

$G(t)=t_1^{64}+18t_1^{32}t_2^{16}+180t_1^{16}t_2^{24}+24t_1^{16}t_3^{16}+432t_1^8t_2^4t_4^{12}+288t_1^8t_2^4t_3^8t_6^4+648t_1^8t_2^{28}+\1344t_1^4t_3^{20}+1440t_1^4t_2^6t_3^4t_6^6+576t_1^4t_3^4t_6^8+2592t_1^4t_2^6t_4^{12}+2349t_1^2t_2t_3^{10}t_6^5+10368t_1^2t_2t_3^2t_6^9+\3456t_1^2t_2t_3^2t_4^3t_6t_{12}^3+512t_1t_3^{21}+4608t_1t_3^5t_6^8+9216t_1t_9^7+873t_2^{32}+1244t_2^8t_6^8+\1296t_2^8t_4^{12}+5760t_2^2t_6^{10}+9576t_4^{16}+5472t_4^4t_{12}^4+11520t_4t_{12}^5+6912t_8^8+3456t_8^2t_{24}^2$

Эти выражения выглядят зубодробительно, но хорошая новость в том, что все это очень легко программируется. NumPy плюс сотня строк на Python решают проблему вычисления цикловых индексов.

Далее давайте оценим число возможных орбит одного цвета (скажем, красного). Для этого воспользуемся теоремой Редфилда — Пойа. Как и раньше, придадим красным ячейкам вес x, а всему остальному — вес 0 и подсчитаем коэффициент при x 16. Он будет равен $5912728301approx6*10^{10}$ .Как мы видим, это число сильно больше 4, которые мы имели в тернарном случае.

Задача «перечисления» и длины орбит

Теперь мы должны найти для каждого из этих 5 912 728 301 типов расстановок красных ячеек орбит «раскрасок», включающих все 4 цвета. Цикловой индекс группы перекрашивания строится так же, как в тернарном случае. По структуре он будет аналогичен цикловому индексу S(4)

$S(t)=frac1{24}(t_1^4+6t_1^2t_2+3t_2^2+8t_1t_3+6t_4)$

Всего в этой группе будет $|S(16)||S(16)||S(16)||S(16)||S(4)|=(16!)^4*4!approx5*10^{54}$ элементов. Не буду полностью выписывать этот, ибо в нем тысячи слагаемых. Это увеличило бы статью в несколько раз, а она и так получается большая

Ограничусь лишь оценкой количества орбит «раскрасок» куба 4x4x4 в 4 цвета. Для этого замечу, что в ряду доминирует первый член - $t^{64}$ , соответствующий случаю, когда все ячейки остаются на месте. Его вклад $64! approx10^{89}$ составляет значительную конечного результата. Таким образом мы с хорошей точностью можем оценить по теореме де Брейна общее число орбит:

$frac{64!}{(16!)^4*(4!)^4*3!}approxfrac{10^{89}}{5*10^{54}*82944}approx 3*10^{29}$

Далее перед нами встает наша задача перечисления. Как из 5912728301 орбит красных ячеек построить все $3* 10^{29}$ ? Перебор по пространству 5 912 728 301x 5 912 728 301x 5 912 728 301 — такая себе история. Кроме этого нужно еще понять, какие типы орбит являются запрещенными. Ну и далее для каждого типа орбит оценить ее длину. Давайте введем функцию . Длина орбиты зависит от типов расстановок (красных, желтых, зеленых и синих ячеек). Было бы прекрасно иметь какой-то простой способ вычисления длины орбиты, исходя из типов этих расстановок. Но в четверичном случае простой перебор $3*10^{29}$ орбит по всей группеэлементов уже не кажется такой уж страшной задачей, по сравнению с другими масштабами. Я сейчас лишь оценю полный вклад верхней строчки как произведение числа орбит на полную (понятно, что в реальности будет меньше) размерность группы симметрии.

$3*10^{29}*1990656approx6*10^{35}$

«Разделение переменных» и вклад второй линии.

В отличие от тернарного кейса (где ее просто не было) в четверичном дает свой вклад вторая линия (строки матрицы смежности 64–128). Этот вклад будет разным для разных типов орбит раскрасок. Но посчитать его довольно легко. Поскольку мы к этому моменту уже определили верхнюю линию, то можем разбить нашу задачу на 4 независящих друг от друга подсетки (остатки от деления на 4 номеров строк и столбцов -0,1,2,3) и искать ответ в виде произведения. Более того, число вариантов, которыми мы можем расположить ячейки во второй линии, зависит только от типа орбиты ячеек соответствующего цвета в линии первой.

Давайте введем функцию Ф(t), аргументом которой будет тип орбиты для верхней линии, а значением — количество вариантов расстановки ячеек соответствующего цвета в линии второй. Плохая новость в том, что аргумент функции может принимать 5 912 728 301 значений, именно столько у нас орбит для одного цвета. Хорошая новость, что значения функции можно подсчитать(или если нам повезет, вычислить) один раз, ибо от цвета они, в силу симметрии задачи, не зависят. Финально, мы получим вклад второй линии в результат.

Несмотря на простоту этой формулы, здесь сложнее провести какую-то оценку. Мои переборные эксперименты показали, что функция Ф может принимать значения от нескольких тысяч до нескольких сотен тысяч. Давайте возьмем оценку 10⁴ (середина диапазона в логарифмическом масштабе). Тогда окончательно получим для второй линии $10^{16}$ .

Вклад двух последних линий.

Как мы уже говорили, в тернарном кейсе вклад двух последних линий — это просто степень двойки. В кватернарном кейсе она равна $2^{16}=656536.$

Для полного числа решений мы получаем грубую оценку.

$6*10^{35}*10^{16}*65536approx4*10^{56}approx2^{185}$

Что как бы говорит нам о том, что 128-битного счетчика для подсчета решений не хватит. Надо заводить 256-битный. А в остальном все просто. Осталось только посчитать.

Результаты челленджа.

Ну а теперь после усиленной математической подготовки давайте перейдем к самому интересному. За 10 месяцев с момента анонса челленджа на Хабре появилось 97 комментариев и 2 статьи. Теперь, после того как я показал, сколько нетривиальной математики можно вытащить из задачки для 7 класса, надеюсь, их будет больше. Первую статью написал @rukhi7, вторую — @qbertych Она объясняла, как решать бинарный кейс Винтика и Шпунтика на квантовом компьютере. И пусть задача использовалась лишь как иллюстрация, сама статья была настолько толковой и подробной, что даже я (предельно далекий от квантовых вычислений) понял, как это работает. Возрадовавшись, я объявил победителя челленджа и выплатил призовой фонд. Но, увы, политика добралась даже до Винтика и Шпунтика — статью пришлось снять. Как честный человек, @qbertych предложил мне вернуть денежку. Но я решил поступить по-другому и позвал его ко-спонсором в продолжение челленджа. Ибо нераскрытых тайн Винтика и Шпунтика еще очень много.

Призовой фонд остается тем же — 50 000 рублей. Только теперь спонсоров у него двое.

Но если раньше постановка задачи была максимально общей, то теперь я готов выделить конкретные вопросы, которые меня интересуют.

Я был бы благодарен за более внятное описание задачи на языке теории групп. Наверняка существует гораздо более "наукообразное" изложение, чем мои полуинтуитивные соображения.
"Структура дефектов" в кватернарном случае. В тернарном кейсе я придумал классификацию орбит, состоящую из трех чисел (вектора), которые сохраняются при преобразованиях группы. Какая должна быть "структура дефектов" в кватернарном случае? Что там сохраняется? Вектор? Тензор? И очень желательно, чтобы в нем было как можно меньше компонент
«Алгоритм перечисления». Мы знаем (хотя при желании можем забыть), сколько всего у нас существует неэквивалентных раскрасок (орбит) для квадрата 3x3 или куба 4x4x4. Как нам взять ровно по одному представителю каждой орбиты?
Вычисление длин орбит. У нас есть конкретная раскраска (представитель орбиты). Можем ли мы вычислить длину орбиты этой раскраски (или количество стабилизаторов), не перебирая все возможные варианты применения элементов группы к этой раскраске?
Вклад второй линии в кватернарном кейсе — существует ли способ вычисления функции Ф(t), характеризующей количество вариантов решений для второй линии в четверичном случае, или нам все-таки придется строить табличку на 5912728301 входов?
И сколько всего будет решений в кватернарном кейсе?
А в более высоких размерностях?

Автор: vvvphoenix

Источник

Информация

Обсуждаемое

Рекомендуем