 Кредит — это когда банк вас грабит и вы ему за это ещё платите.
Кредит — это когда банк вас грабит и вы ему за это ещё платите.
Пожарный Сидоров бездействовал: банк горел — кредит гасился.
Привет!
Многие из вас, наверняка, слышали не раз подобные шутки про кредиты и ипотеку. Некоторые, наверное, не раз пользовались калькуляторами вкладов и кредитов, и оценивали выгодность того или иного способа накопления денег. Я тоже недавно заинтересовался этой темой, и подошёл к этой проблеме математически.
Постановка задачи
Программист Вася имеет стабильную работу и зарплату. Всё это время он вёл беззаботную жизнь, и не думал о накоплениях, но недавно Вася женился, и стал задумываться о собственном жилье. Подумал он, и решил, что может стабильно откладывать B руб. в месяц. Сейчас квартира стоит S руб. В стране стабильная инфляция H %. Проценты по вкладу — F %, а по кредиту G %. Вклад с капитализацией раз в месяц.
Персонажи вымышлены, все совпадения случайны.
Найти
Как лучше поступить Васе — откладывать деньги в банк или взять кредит? Насколько выгоднее?
Ограничения
В задаче не учитываются различные другие обстоятельства. Например, необходимость платить за съёмную квартиру, на период накопления, о возможности индексации с инфляцией зарплаты, а следовательно выплат. Так же, не учитывается изменения инфляции и процентных ставок, комиссии. Оставлены в стороне и вопросы о надёжности банков и другие жизненные обстоятельства.
Решение
Так как у Васи фиксированная сумма пополнений, то мы можем рассмотреть выгодность того или иного способа приобретения жилья, найдя количество месяцев, которые ему придётся выделять эту сумму, до полной выплаты суммы жилья.
n — это количество месяцев, за которые Вася накопит на жильё.
m — это количество месяцев, которые Вася будет выплачивать кредит.
Тогда из отношения m/n мы сможем судить о выгодности, того или иного способа в m/n раз.
Введём коэффициенты:
f = 1 + F/(100*12)
g = 1 — G/(100*12)
h = 1 + H/(100*12)
это ежемесячные коэффициенты преумножения/потери суммы вклада/ценности/стоимости.
Рассмотрим, как будет изменяться сумма вклада в конце каждый месяца:
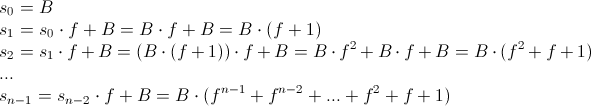
Используя формулу:
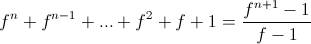
найдём, что сумма в конце срока будет равна:
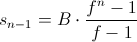
Но за n-месяцев квартира успела подорожать за счёт инфляции. Найдём её стоимость:
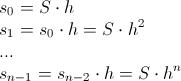
Итого:
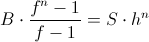
В случае кредита, формулы будут аналогичны, с той лишь разницей, что деньги теряют стоимость, и процент по кредиту это компенсирует:
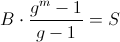
Из двух выше описанных формул, выведем, что:
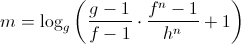
Таким образом, мы вывели общую формулу выгодности вклада/кредита в зависимости от их сроков:
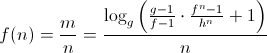
Пример 1 — либеральный
Я взял следующие реальные цифры в качестве примера:
Процент по вкладу: F = 10% годовых.
Процент по кредиту: G = 12.5% годовых.
Уровень инфляции: H = 8.7% годовых (взял как среднее за 2008-2012)
Вася может позволить себе выделить B = 40000 руб./мес.
Вася очень хочет купить квартиру стоимостью S = 2 733 000 руб.
В итоге получился такой вот график (спасибо сервису yotx.ru):
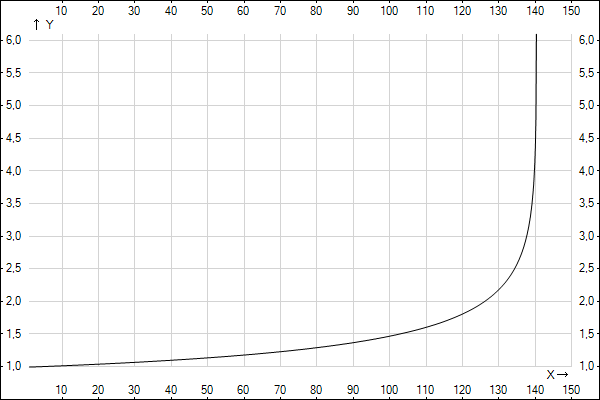
Как видно, логично, что чем меньше срок вклада/кредита, тем меньше между ними разница. Кроме того у графика есть асимптота, при значении n=140. Это говорит о том, что никакими способами нельзя выплатить кредит на ту же сумму, таким же размером ежемесячного платежа, как если бы Вася откладывал на вклад. То есть это предел кредитования, и следовательно нужную сумму Вася может накопить только вкладом.
Например, если Вася возьмёт кредит 2 733 000 руб. на 10 лет (120 мес.), то ему нужно будет выплачивать как раз по 40 000 руб. Банковским вкладом, он накопит нужную сумму с учётом инфляции (5 160 834 руб.) за 88 месяцев. Итого 120/88 = 1.36, что сходится с графиком.
Взять кредит сумму, более чем 3 833 000 руб. (эта цена через 140 мес. превратится в 10 538 000 руб. за счёт инфляции, именно эта сумма будет на счёте к тому времени) Вася позволить себе не сможет, т. к. при том же размере ежемесячных выплат выплатить кредит невозможно, как бы он не растягивал срок.
Пример 2 — экзотический
Рассмотрим тот же пример, но поменяем лишь размер инфляции:
Уровень инфляции: H = 11% годовых
Стоит отметить, что данный вариант маловероятен, т. к. обычно процентная ставка по вкладам всегда выше уровня инфляции. Хотя и не всегда.
Получаем график:
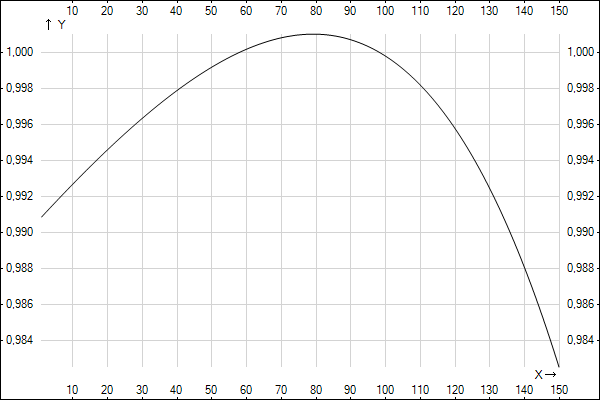
Тут получается интересная ситуация, когда вклад выгоден только на промежутке ~58-97 месяцев, во всех остальных случаях брать кредит выгоднее.
Например, Вася возьмёт те же 2 733 000 руб. в кредит. Банковским вкладом, он накопит нужную сумму с учётом инфляции (8 169 345 руб.) практически за те же 120 месяцев.
Пример 3 — грабительский
Рассмотрим другой реалистичный пример, современный потребительский кредит. Данные как в примере 1, но поменяем процентную ставку по кредиту:
Процент по вкладу: F = 10% годовых.
Процент по кредиту: G = 20% годовых.
Уровень инфляции: H = 8.7% годовых.
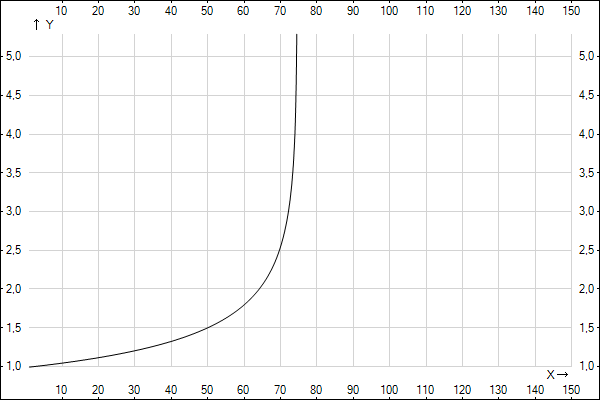
Как видим, Васе тут уже тяжелее, т. к. кредит на таких условиях больше чем на 6 лет брать ему становится очень затратно, по сравнению с вкладом. А предел кредитования для Васи гораздо меньше — 2 400 000, то есть желаемую квартиру Васе уже не купить в кредит, даже за 50 лет
Заключение
Так всё же, стоит ли брать кредиты? Решать, конечно же, вам. У кредитов есть, преимущество — вы получаете желаемое уже сейчас, следовательно, вы можете уже пользоваться вашей новенькой квартирой, а не ждать 10 лет, поэтому даже 1,5x-2x переплата в этом случае не так страшна, особенно если приходится платить аренду за чужую квартиру всё это время. С другой стороны, в нашей жизни нет никаких гарантий, что условия задачи будут стабильными как в примерах, и тут главное не выйти за асимптоту, иначе кредит будет попросту непосильной ношей.
Ну и напоследок опрос по теме.
Автор: PaulZi






