7 красивейших интегралов с экзамена в Школу Анализа Данных от Яндекса

2025-01-05 в 7:18, admin, рубрики: задачи, интеграл, матан, математика, поступление, ШАД, школа анализа данных

С интегралами начинают знакомится еще в старших классах, продолжают их изучать в университете. В основном все задачи на интегрирование в курсах школы и университетов счетные, но в этой статье мы постарались собрать самые интересные и красивые задачи, по нашему скромному мнению. Отчасти красота состоит в том, что для их решение вам нужна лишь смекалка, пытливость ума и знание, что интеграл от функции на отрезке от до b

( $int_{a}^{b} f(x)dx$ ) — это просто площадь под графиком функции . Поэтому перед тем, как

открыть решение обязательно попробуйте порешать самостоятельно!

Задача 1

Вычислите, чему равно выражение $int_{-1}^{1} frac{3^x-1}{3^x+1} dx$

Подсказка

Если бы задача была чисто счетная, то в этой статье она бы не оказалась, поэтому стоит найти красивую идею и что-то заметить. Давайте рассуждать конструктивно: интеграл состоит из отрезка интегрирования и подинтегральной функции. Что особенного можно про них сказать? Можно заметить, что отрезок интегрирования симметричен относительно 0. А какими свойствами обладает подынтегральная функция, какие вообще классы функций мы знаем еще со школы? Несложно заметить, что функция нечетная, то есть (проверяется непосредственно). Что можно сказать про интеграл от нечетной функции, взятый по симметричному промежутку?

Решение

Несложно проверить, что подинтегральная функция нечетная: .

Действительно, $f(-x)=frac{3^{-x}-1}{3^{-x}+1}$ .

Домножим числитель и знаменатель на и получим

$f(-x)=frac{3^{-x}-1}{3^{-x}+1}=frac{1 - 3^x}{1 + 3^x}=- frac{3^x - 1}{1 + 3^x}=- f(x)$

Также заметим, что интеграл берется по симметричному относительно нуля отрезку. Известно, что интеграл от нечетной функции по симметричному относительно нуля промежутку равен . Это очевидно, если нарисовать график нечетной функции.

7 красивейших интегралов с экзамена в Школу Анализа Данных от Яндекса - 12

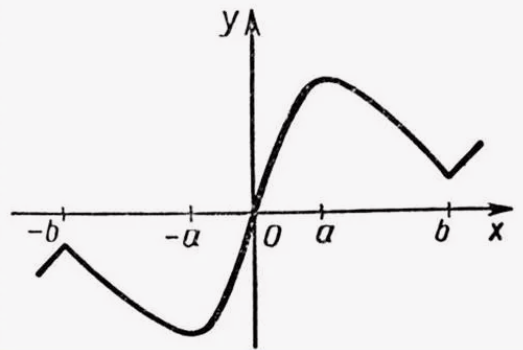
Видим, что площадь отдо равна по модулю площади под графиком от до. Но вот эти площади противоположны по знаку, а значит если мы их сложим, то получим 0.

Ответ

Задача 2

Пусть . Докажите, что $int_{a}^{b} (x^2+1)e^{-x^2} dx ge e^{-a^2} - e^{-b^2}$

Подсказка

Воспользуйтесь фактом, что если на отрезке,то интеграл

$int_{a}^{b} f(x)dx ge 0$ . Что очевидно, ибо интеграл = площадь, а площадь

под графиком неотрицательной функции не может быть меньше нуля.

Или можно воспользоваться более общим фактом, что если на отрезке , то

$int_{a}^{b} f(x)dx ge int_{a}^{b} g(x)dx$ .

Это тоже очевидно, если просто нарисовать картинку. Если один график выше другого, то и площадь под ними будет больше площади под другим графиком.

Решение

Так как (полный квадрат ${(x - 1)}^2 ge 0$ ), то (воспользуемся монотонностью интеграла)

$int_{a}^{b} (x^2+1)e^{-x^2} dx geq int_{a}^{b} 2xe^{-x^2} dx$

Теперь вычислим последний интеграл, для этого занесем под знак дифференциала.

$int_{a}^{b} 2xe^{-x^2} dx=int_{a}^{b} e^{-x^2} dx^2=e^{-a^2} - e^{-b^2}$

Задача 3

Вычислите, чему равно выражение

$int_{1}^{e} sqrt{ln(x)} dx +int_{0}^{1} e^{x^2} dx$

Подсказка

Вычислить интегралы по отдельности и сложить результаты кажется невозможным. Значит похоже они как-то связаны.. Давайте подумаем, как связаны подинтегральные функции и промежутки интегрирования. Пусть $y=e^{x^2}$ , попробуем изобразить график на плоскости . Заметим, что . То есть принимаются такие же значения как концы промежутка интегрирования первой функции, логарифма.

Решение

Это наводит на следующую мысль, что является обратной функцией к $e^{x^2}$ .

Действительно, пусть $y=e^{x^2}$ , выразим x через y:

$ln(y)=ln(e^{x^2})$

То есть у нас была зависимость , а мы построили зависимость .

Изобразим эти два графика на плоскости . Только пусть , а $x(y)=e^{y^2}$ .

7 красивейших интегралов с экзамена в Школу Анализа Данных от Яндекса - 48

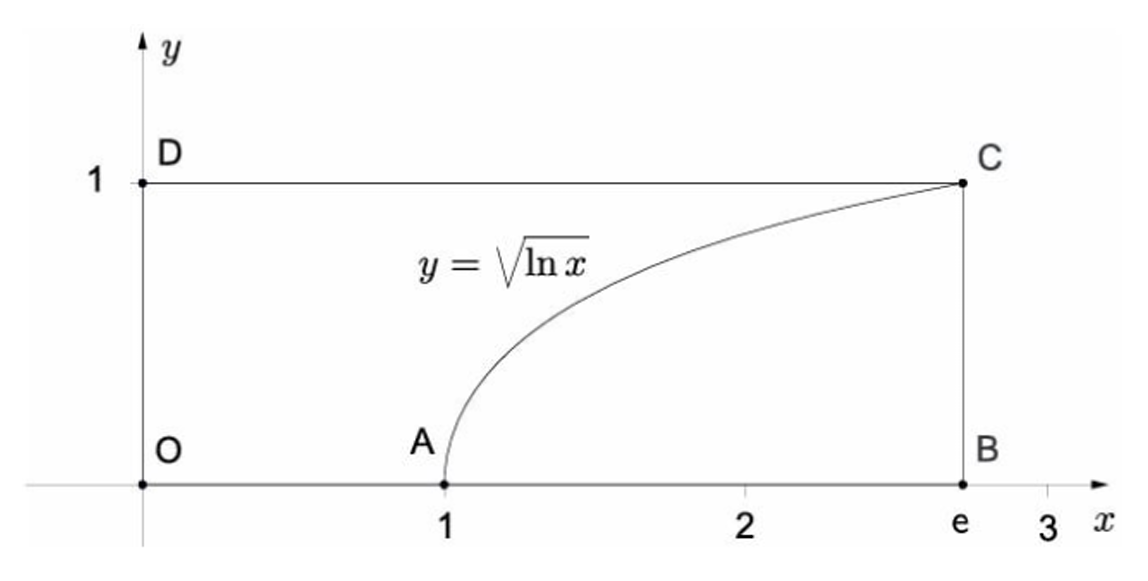
Вспомним, что интеграл = площадь, тогда видим, что площади под этими графиками в сумме дают весь прямоугольник, чья площадь равна .

Ответ

Задача 4

Вычислить, чему равно выражение

$int_{0}^{2pi} mathrm{sin}{(mathrm{sin}{x}+2025x)} dx$

Подсказка

Заметьте, что подынтегральная функция периодична, а также она нечетная.

Решение

Подынтегральная функция нечётная, что проверяется непосредственно.

Также подынтегральная функция имеет период, то есть для всякого . Проверим это, просто зная, что период синуса

Очевидно, если нарисовать картинку, интеграл от переодичной функции, по промежутку, чья длина равна периоду этой функции, не зависит от расположения этого промежутка на числовой прямой.

То есть $int_{0}^{2pi} f(x)dx=int_{-pi}^{pi} f(x)dx$ , а последний интеграл равен нулю из-за

нечётности функции .

Ответ

Задача 5

Вычислить, чему равно выражение

$int_{0}^{frac{pi}{2}} frac{dx}{1+tg^{a}x} dx$

Подсказка

Попробуйте посмотреть на интеграл $int_{0}^{frac{pi}{2}} frac{dx}{1+ctg^{a}x} dx$

Решение

Давайте думать конструктивно. Этот интеграл вручную вычислить не получится. Давайте попробуем привлечь наш опыт решения математических задач. Как можно вообще что-то вычислить? Обычно либо мы вычисляем что-то напрямую, либо составляем уравнение с этим неизвестным (что хотим найти) и решаем его. Но как нам составить уравнение на этот интеграл? Давайте подумаем с чем у нас вообще может быть связан тангенс.. Конечно же с котангенсом. Тогда появляется идея посмотреть на интеграл

$I=int_{0}^{frac{pi}{2}} frac{dx}{1+ctg^{a}x} dx$

Оказывается этот интеграл равен исходному. Это можно доказать сделав в исходном интеграле замену $x=frac{pi}{2} - t$ :

$int_{frac{pi}{2}}^{0} frac{dx}{1+ctg^{a}t} d(frac{pi}{2} -t)=int_{0}^{frac{pi}{2}} frac{dt}{1+ctg^{a}t} d(t)=int_{0}^{frac{pi}{2}} frac{dx}{1+ctg^{a}x} dx$

Пояснения:

Первый интеграл - просто сделали подстановку, посмотрите внимательно, как изменились пределы интегрирования. Просто, если , то $t=frac{pi}{2}$ , а если $x=frac{pi}{2}$ , то .

Второй интеграл равен первому: просто вынесли минус из дифференциала и поменяли пределы интегрирования, что тоже дало минус перед интегралом. Итого минус на минус равно плюс.

Третий интеграл равен второму, потому что в третьем интеграле мы просто заменили букву на букву . Поэтому какая разница, интеграл же просто есть площадь!

Давайте теперь просто сложим эти два равных интеграла:

$int_{0}^{frac{pi}{2}}frac{dx}{1+tg^{a}x} + int_{0}^{frac{pi}{2}}frac{dt}{1+ctg^{a}t}=int_{0}^{frac{pi}{2}}(frac{1}{1+tg^{a}t}+frac{1}{1+ctg^{a}t})dt$

Поскольку $frac{1}{1+tg^{a}t}+frac{1}{1+ctg^{a}t}=frac{2+tg^{a}t+ctg^{a}t}{1+1+tg^{a}t+ctg^{a}t}=1$ , то выходит уравнение

$2I=frac{pi}{2}$ . Итого $I=frac{pi}{4}$ .

Ответ

$frac{pi}{4}$

Задача 6

Вычислить, чему равно выражение

$int_{0}^{frac{pi}{2}}(mathrm{sin^2}{(mathrm{sin}{x})}+mathrm{cos^2}{(mathrm{cos}{x})})dx$

Подсказка

К этой задаче можно подойти по-разному. Можно аналогично предыдущей задаче сделать замену $x=frac{pi}{2} - t$ и сложить два получившихся интеграла. Можно попробовать примерно нарисовать график и заметить, что функция нечетна относительно точки $(frac{pi}{4};1)$ . В решение покажу немного другой подход.

Решение

Несложно заметить, что если - непрерывная функция, то

$int_{0}^{frac{pi}{2}}f(mathrm{sin}{x})dx=int_{0}^{frac{pi}{2}}f(mathrm{cos}{x})dx$ . Достаточно просто нарисовать картинку и

понять, что кривуюмы проходим в случае синуса слева направо, а в случае косинуса - справа налево.

Тогда

$int_{0}^{frac{pi}{2}}(mathrm{sin^2}{(mathrm{sin}{x})}+mathrm{cos^2}{(mathrm{cos}{x})})dx=int_{0}^{frac{pi}{2}}(mathrm{sin^2}{(mathrm{sin}{x})}+mathrm{cos^2}{(mathrm{sin}{x})})dx=int_{0}^{frac{pi}{2}} 1 dx$

Итого ответ $frac{pi}{2}$ . Примерно такое же решение можно получить, если сделать замену в исходном интеграле $x=frac{pi}{2} - t$ .

Ответ

$frac{pi}{2}$

Задача 7

Вычислить чему равно выражение

$I_n=int_{0}^{infty} lambda x^n e^{-lambda x}dx$

Подсказка

Воспользуйтесь формулой интегрирования по частям.

7 красивейших интегралов с экзамена в Школу Анализа Данных от Яндекса - 85

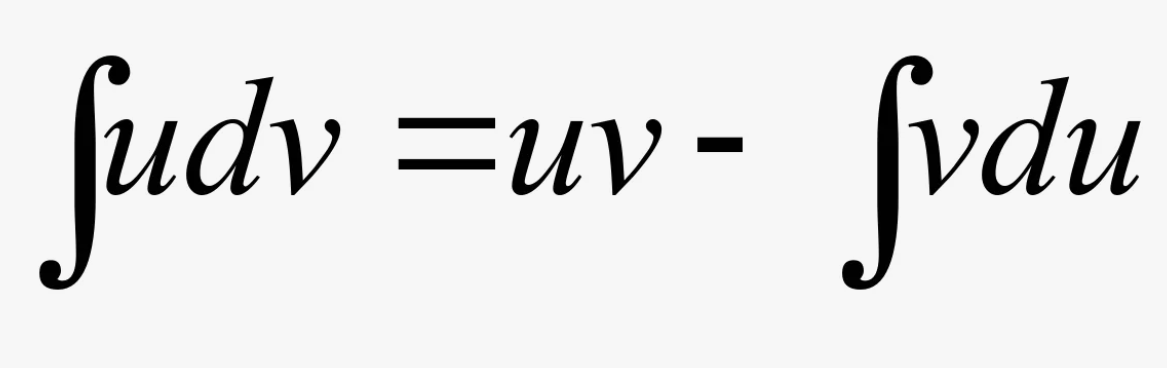
Также напомню, как можно понимать дифференциал при интегрировании. , где - производная функции.

Решение

Данный интеграл является -ым моментом экспоненциального распределения.

Попробуем вычислить частные случай. Занесем экспоненту под дифференциал и воспользуемся формулой интегрирования по частям из подсказки.

$int_{0}^{infty} lambda x e^{-lambda x}dx=- int_{0}^{infty} x d(e^{-lambda x})=- (|_{0}^{infty} xe^{-lambda x} - int_{0}^{infty} e^{-lambda x}dx)$

Первое выражение равно 0. Действительно, если "подставить" в выражение бесконечность, то экспонента уведет все в 0, а если подставить ноль, то экспонента умножится на ноль и будет ноль. Второе же выражение с учетом минуса перед скобками равно $frac{1}{lambda}$ .

Попробуем вычислить частный случай .

$int_{0}^{infty} lambda x^2 e^{-lambda x}dx=-int_{0}^{infty} x^2d(e^{-lambda x})=- (|_{0}^{infty}x^2 e^{-lambda x} - int_{0}^{infty} e^{-lambda x}d(x^2))$

Аналогично занесли экспоненту под дифференциал. Первое выражение при подстановке пределов обнуляется. Вычислим второе выражение, раскрыв дифференциал как

$int_{0}^{infty} 2x e^{-lambda x}dx=frac{2}{lambda} int_{0}^{infty} lambda x e^{-lambda x}dx$

Последний интеграл мы уже вычисляли, то есть $I_2=frac{2}{lambda^2}$ .

Аналогично можно вычислить просто загоняя экспоненту под дифференциал и пользуясь формулой интегрирования по частям.

$I_n=int_{0}^{infty} lambda x^n e^{-lambda x}dx=-int_{0}^{infty} x^nd(e^{-lambda x})=- (|_{0}^{infty}x^n e^{-lambda x} - int_{0}^{infty} e^{-lambda x}d(x^n))$