Привет! Недавно столкнулся с задачей подсчёта числа Пи до знака, номер которого будет выбирать пользователь. Сразу полез на Википедию, почитать, что за зверь такой, это Пи, и как его находить с заданной точностью. Формул, описывающих число Пи, уйма. Но для решения моей задачи всё в этих формулах упирается либо в точность и длину базовых типов языка (я выбрал Java), либо (для решения предыдущей проблемы) в длинную арифметику, которую мне реализовывать не очень-то хотелось. Хотелось найти какой-то алгоритм, позволяющий найти число Пи вплоть до заданного знака, причём ровно до этого знака, а не находить длиннющее число, а потом обрезать его, чтобы отдать пользователю то, что он просил.
И я нашёл такой алгоритм, тот самый алгоритм «краника». Слово краник звучит здесь странно, но я не нашёл лучшего способа перевести название этого алгоритма с английского, как перевести дословно. Вообще, в оригинале это звучит как «A Spigot Algorithm for the Digits of Pi». Авторами алгоритма и его нарицателями являются американские математики Стенли Рабинович (Stanley Rabinowitz) и Стен Вэгон (Stan Wagon). Создали свой алгоритм для нахождения цифр числа Пи эти два товарища в 1995 году. Сама же идея алгоритма вышла из-под пера некого Сейла (Sale) ещё в 1968 году, и предназначался тот алгоритм для нахождения цифр числа e.
Вообще, англо-русские словари дают перевод слова spigot как “втулка”. Этот перевод ясности не даёт никакой. Поэтому я перевёл это слово как «краник», так как spigot в английском языке описывается как механизм, регулирующий поток жидкости. Идея же алгоритма в том и заключается, что за одну итерацию мы получаем ровно одну цифру числа Пи и потом её не используем. То есть цифры как бы вытекают из алгоритма, как вода из крана.
Теперь сам алгоритм. Я не буду вдоваться во всю математику (чего я, собственно, и не делал, разбирая алгоритм), подробнее о нём вы можете почитать здесь. К слову, по этой ссылке, есть и реализация алгоритма для поиска 1000 цифр числа Пи на Паскале, которой я по своей лени и решил сразу же воспользоваться. Переписал на Java, ан нет — не заработало. Выводило какую-то непонятную мне белиберду. Я это дело и бросил, так как отлаживать код, которого не понимаешь, сами знаете, как тушить горящее масло водой. Поэтому решил-таки разобраться с алгоритмом самолично.
Для нахождения n знаков числа Пи, понадобится массив длиной [10 * n / 3]. Причём целых чисел. Особенность алгоритма в том, что используется только целочисленная арифметика. Инициализируем все ячейки массива числом 2.
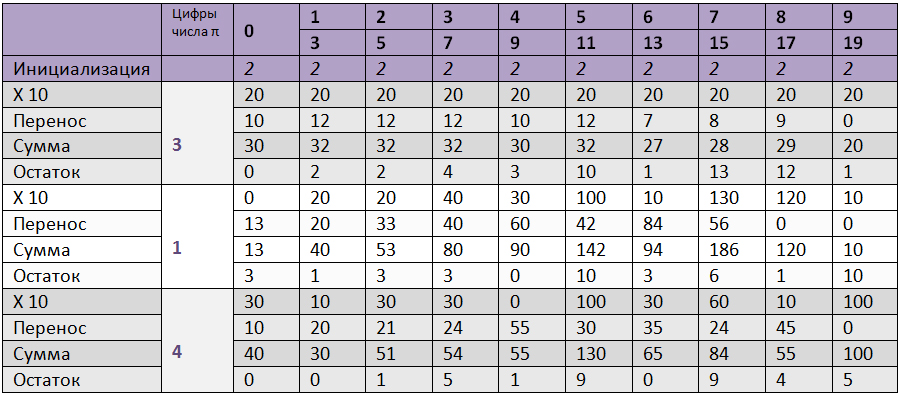
Далее, чтобы найти одну цифру числа Пи, необходимо пройтись по всем ячейкам массива с конца к началу и выполнить несложные действия. На примере таблицы, рассмотрим всё по порядку. Допустим, мы хотим найти 3 цифры числа Пи. Для этого нам необходимо зарезервировать 3 * 10 / 3 = 10 ячеек целого типа. Заполняем их все числом 2. Теперь приступим к поиску первой цифры…
Начинаем с конца массива. Берём последний элемент (под номером 9, если начинать счёт с 0. Этот же номер будем называть нумератором, а тот, что под ним в таблицу – денумератором) — он равен 2. Умножаем его на 10 (2 * 10 = 20). К получившемуся числу 20 прибавляем число из ячейки «Перенос» – число, которое переносится из более правой операции. Разумеется, правее мы ничего не считали, поэтому это число равно 0. Результат записываем в «сумму». В «остаток» записываем остаток от деления суммы на денумератор: 20 mod 19 = 1. А сейчас считаем «перенос» для следующего шага. Он будет равен результату деления суммы на дунумератор, умноженному на нумератор: (20 / 19) * 9 = 9. И записываем полученное число в ячейку с «переносом», стоящую левее от текущего столбца. Проделываем те же действия с каждым элементом массива (умножить на 10, посчитать сумму, остаток и перенос на следующий шаг), пока не дойдём до элемента с номером 0. Здесь действия немного отличаются. Итак, посмотрим, что у нас в таблице. Под нулём – элемент массива, равный 2, и перенос из предыдущего шага, равный 10. Как и в предыдущих шагах, умножаем элемент массива на 10 и прибавляем к нему перенос. В сумме получили 30. А сейчас делим сумму не на денумератор, а на 10 (!). В итоге получаем 30 / 10 = 3 + 0 (где 0 – остаток). Полученное число 3 и будет той заветной первой цифрой числа Пи. А остаток 0 записываем в отведённую ему ячейку. Для чего были остатки? Их нужно использовать в следующей итерации – чтобы найти следующую цифру числа Пи. Поэтому разумно сохранять остатки в наш изначальный массив размером 10 * n / 3. Таким образом, видно, что возможности алгоритма упираются именно в размер этого массива. Поэтому число найденных цифр ограничивается доступной памятью компьютера либо языком, на котором вы реализуете алгоритм (конечно, языковые ограничения можно обойти).
Но это не всё. Есть один нюанс. В конце каждой итерации может возникать ситуация переполнения. Т.е. в нулевом столбце в «сумме» мы получим число, большее, чем 100 (эта ситуация возникает довольно редко). Тогда следующей цифрой Пи получается 10. Странно, да? Ведь цифр в десятичной системе счисления всего от 0 до 9. В этом случае вместо 10 нужно писать 0, а предыдущую цифру увеличивать на 1 (и стоящую перед последней, если последняя равна 9, и т.д.). Таким образом, появление одной десятки, может изменить одну и больше найденных ранее цифр. Как отслеживать такие ситуации? Необходимо найденную новую цифру первоначально считать недействительной. Для этого достаточно завести одну переменную, которая будет считать количество недействительных цифр. Нашли одну цифру – увеличили количество недействительных цифр на 1. Если следующая найденная цифра не равна ни 9, ни 10, то начинаем считать найденные ранее цифры (и помеченные как недействительные) действительными, т.е. сбрасываем количество недействительных цифр в 0, а найденную новую цифру начинаем считать недействительной (т.е. можно сразу сбрасывать в 1). Если следующая найденная цифра равна 9, то увеличиваем количество недействительных цифр на 1. Если же следующая цифра 10, то увеличиваем все недействительные цифры на 1, вместо 10 записываем 0 и этот 0 считаем недействительным. Если эти ситуации не отслеживать, то будут появляться единичные неверные цифры (или больше).
Вот и весь алгоритм, который авторы сравнили с краном. Ниже привожу код метода, реализованного на Java, который возвращает строку с числом Пи.
public static String piSpigot(final int n) {
// найденные цифры сразу же будем записывать в StringBuilder
StringBuilder pi = new StringBuilder(n);
int boxes = n * 10 / 3; // размер массива
int reminders[] = new int[boxes];
// инициализируем масив двойками
for (int i = 0; i < boxes; i++) {
reminders[i] = 2;
}
int heldDigits = 0; // счётчик временно недействительных цифр
for (int i = 0; i < n; i++) {
int carriedOver = 0; // перенос на следующий шаг
int sum = 0;
for (int j = boxes - 1; j >= 0; j--) {
reminders[j] *= 10;
sum = reminders[j] + carriedOver;
int quotient = sum / (j * 2 + 1); // результат деления суммы на денумератор
reminders[j] = sum % (j * 2 + 1); // остаток от деления суммы на денумератор
carriedOver = quotient * j; // j - нумератор
}
reminders[0] = sum % 10;
int q = sum / 10; // новая цифра числа Пи
// регулировка недействительных цифр
if (q == 9) {
heldDigits++;
} else if (q == 10) {
q = 0;
for (int k = 1; k <= heldDigits; k++) {
int replaced = Integer.parseInt(pi.substring(i - k, i - k + 1));
if (replaced == 9) {
replaced = 0;
} else {
replaced++;
}
pi.deleteCharAt(i - k);
pi.insert(i - k, replaced);
}
heldDigits = 1;
} else {
heldDigits = 1;
}
pi.append(q); // сохраняем найденную цифру
}
if (pi.length() >= 2) {
pi.insert(1, '.'); // добавляем в строчку точку после 3
}
return pi.toString();
}
Ради интереса провёл тест производительности алгоритма в зависимосты от величины n (количество цифр, которые нужно найти). Получился вот такой график:
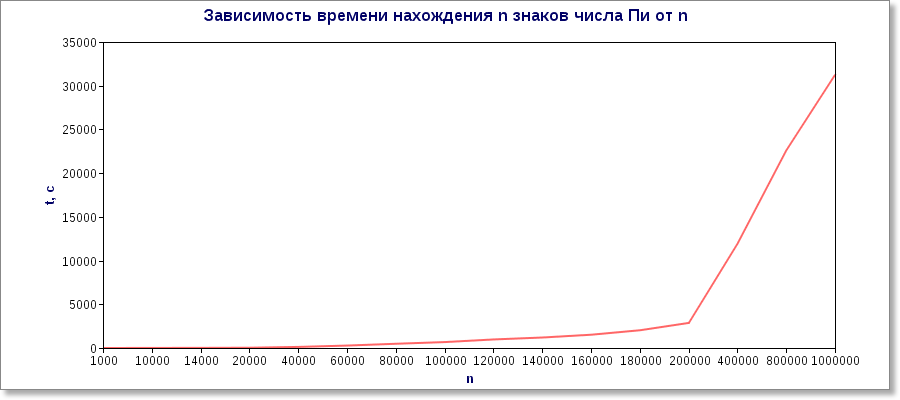
Для нахождения миллиона цифр понадобилось больше восьми с половиной часов. Тесты я проводил без печати результатов и использовал не StringBuilder, а байтовый массив.
Итак, подытожим. Главными достоинствами алгоритма являются его простота (посчитать можно без проблем и руками), а также использование только целочисленной арифметики, что ускоряет процесс вычислений и добавляет точности. Главным же недостатком я считаю ограниченность алгоритма (памятью).
http://en.wikipedia.org/wiki/Pi
http://en.wikipedia.org/wiki/Spigot_algorithm
http://www.mathpropress.com/stan/bibliography/spigot.pdf
http://www.pi314.net/eng/goutte.php
Автор: yahorfilipcyk





