Мы привыкли считать, что математика – это инструмент, который позволяет другим наукам более точно описывать окружающий мир и порой находить закономерности там, где их не было видно с первого взгляда. Однако сегодня мы поговорим о том, как случилось обратное и забавный географический казус привел к появлению совершенно нового раздела математики.
Если спросить гугл «Какова длина береговой линии озера Байкал?», то на разных сайтах вам предложат разные варианты ответов: от 1850 до 2100+ километров. Вас ничего не смущает? Да, расхождение данных составляет более 250 км! *Те, кто знает, в чем фокус, просьба не спойлерить*. Но как же так вышло, неужели у нас люди настолько безалаберно относятся к географическим измерениям? Однако с той же самой проблемой столкнулся Льюис Фрай Ричардсон еще в начале XX века.
Ричардсон был сам по себе очень интересный человек: английский ученый, увлекающийся всем подряд от математики (может, кто слышал про зубодробительную экстраполяцию Ричардсона) до метеорологии (его работы в этой области являются основой современного прогнозирования погоды). Кроме того, он был одним из первых изобретателей эхолокационного способа обнаружения айсбергов – настолько сильно человек впечатлился трагедией Титаника. В общем, везде успел засветиться. Но не будем останавливаться на его личности, а то тут можно писать отдельную статью, скажем только, что Ричардсон был вдобавок ко всему глубоко убежденным пацифистом, поэтому его исследования часто затрагивали теоретические причины военных конфликтов.
Пытаясь понять, зависит ли вероятность войны между двумя странами от протяженности их общей границы, он заметил существенное расхождение значений из разных источников. По официальным данным испанцев, длина их границы с Португалией составляла 987 километров, а португальцы измеряли ее как 1214 километров. Снова разброс 200+ км. Так какое значение брать для исследования? Кажется, у европейцев тоже были проблемы со счетом…
Секрета здесь никакого нет, и как большинство уже догадалось, ответ кроется в инструменте измерения: чем меньше ваша, так сказать, «линейка», тем больше неровностей рельефа можно учесть. Так что неправильных данных нет (впрочем, так же, как и правильных), и португальцы, по всей видимости, использовали линейку покороче, чем испанцы. То же самое относится и к береговой линии Байкала: чтобы знать ее длину, нужно обязательно указать масштаб карты, по которой производились расчеты, ведь чем больше масштаб – тем больше заливов, бухточек и изгибов на нем отображается.
*Ну да, ну да, я понимаю, что это всё очевидно, но прелюдия – вещь обязательная*
Ричардсон, разумеется, тоже сразу понял, в чем дело, но, в отличие от его предшественников, которые не обращали внимания на расхождения в данных, его самого этот факт сильно зацепил. В своей статье, опубликованной в 1961 году, он сделал вывод, что при уменьшении единицы измерения длина береговой или пограничной линии стремится к бесконечности и не имеет фиксированного значения в принципе *только если вы по атомам всё мерить не начнете*.
Как это часто бывает, тогда на статью не обратили особого внимания, а вот сегодня это удивительное открытие называют эффектом Ричардсона или парадоксом береговой линии. Вот так. Спасибо за внимание, ставьте лайки, подписы…. Ах да, вроде бы речь шла про математику. Каким образом среди линеек, карт и испанцев с португальцами она тут затесалась?
Дело в том, что сам того не осознавая, Ричардсон стал первооткрывателем новой дисциплины. Шесть лет спустя в статье журнала Science математик Бенуа Мандельброт вновь подробно описал парадокс береговой линии, а в 1975 году придумал название для таких бесконечно сложных объектов, как ломаная граница побережий. Так родилось красивое слово – фрактал.
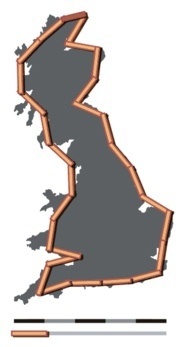
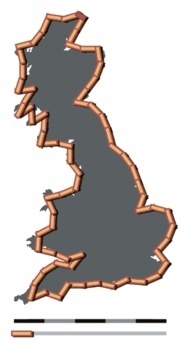
Объекту, чтобы заслужить звание фрактала, достаточно иметь сложную структуру, вне зависимости от масштаба рассмотрения – вот самое понятное (но и самое дилетантское) определение данного термина. В реальном мире, мы, разумеется, не можем бесконечно увеличивать масштаб или бесконечно уменьшать единицы измерения, но все-таки испано-португальская граница является достаточно близким аналогом фрактала, к тому же очень наглядным.
Мандельброт, с упоением развивавший неизведанную область математики, называл ее «прекрасной, чертовски трудной и с каждым днем все более ценной». Вслед за ним потянулись и другие ученые, открывая все новые и новые виды фракталов, уже чисто математических.
Пример одного такого фрактала наверняка многие знают, он даже появлялся где-то на обложке учебника – это снежинка или кривая Коха. Забавно, что сам Хельге фон Кох описал данную фигуру еще в 1904 году, правда, для него это была всего лишь занимательная математическая гимнастика, не более. Ее легко построить: делим отрезок на три части, на центральной части строим равносторонний треугольник, стираем основание и повторяем действия сначала на всех получившихся новых отрезках.
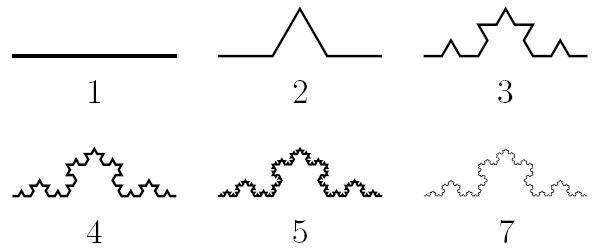
Если мы возьмем и соединим концы этой кривой, то получим красивую снежинку, которую назвали снежинкой Коха *как неожиданно*. При этом, полученная фигура все еще имеет бесконечную длину! – как ни приближай ее, как ни увеличивай масштаб, вы всегда будете наблюдать сложную изрезанную границу. Совсем как с береговой линией Байкала. Кстати, этот факт является одним из крайне интересных свойств замкнутых фракталов – кривая, образующая их, имеет бесконечную длину, но при этом ограничивает точно вычисляемую конечную площадь, ведь и снежинку Коха, и озеро Байкал можно полностью уместить в круг.
Так что, если площадь поверхности Байкала можно довольно точно измерить, то длина его берегов в разных источниках будет отличаться. Подумайте над этим, если вы учитель географии, и вам приспичило помучить кого-то из учеников каверзными вопросами.
Автор: Александр Грибоедов
Автор: CatScience






