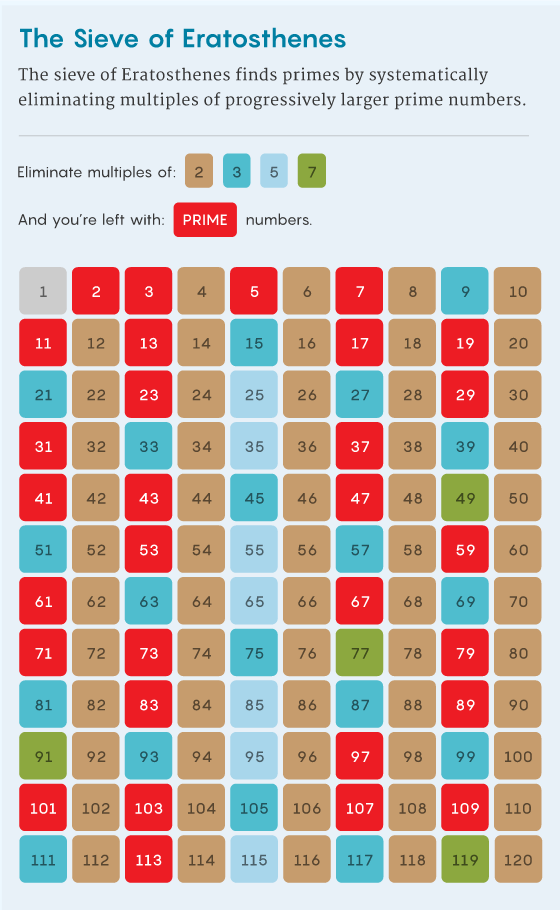
Более 2,000 лет назад греческий математик Эратосфен разработал метод поиска простых чисел, получивший название решето Эратосфена, который остаётся актуальным по сей день. Его идея заключалась в том, чтобы определять простые числа вплоть до заданной точки путём постепенного «отсеивания» тех, которые таковыми не являются. Начинается отсев с вычёркивания всех чисел, кратных 2 (кроме самой 2), затем кратных 3 (кроме 3). Следующее число, 4, уже оказывается вычеркнуто, значит, очередным шагом идёт вычёркивание всех чисел, кратных 5 и так далее. Все оставшиеся в итоге числа считаются простыми, то есть такими, которые делятся только на 1 и на самих себя.
Эратосфен работал со всем множеством простых чисел, но вы можете использовать вариации его метода для поиска таких, которые будут обладать особыми свойствами. Хотите найти «близнецов», которые отличаются всего на 2 единицы, например, 11 и 13 или 599 и 601? Для этого есть свой отсев. Интересуют простые числа, которые на 1 больше полного квадрата, например, 17 или 257? И для этого тоже есть свой отсев.
Современные методы отсева послужили катализатором крупнейших открытий в теории чисел, начиная с Великой теоремы Ферма и заканчивая до сих пор недоказанной гипотезой о простых-близнецах, которая гласит, что существует бесконечное число пар таких близнецов. Методы отсева, описанные венгерским математиком Палом Эрдешом в 1965 году, «являются, пожалуй, самым мощным элементарным инструментом в теории чисел».
Хотя эта мощь ограничивается степенью понимания математиками того, как простые числа распределяются вдоль числовой оси. Несложно выполнить отсев в пределах небольшого числа, например, 100. Но математики хотят понять, как процесс отсева действует для больших чисел. Причём они не могут вывести все числа, оставшиеся после отсева до некоего экстремального значения. Вместо этого они пытаются оценить, сколько чисел примерно окажется в этом списке.
В случае отсева по Эратосфену эта оценка будет зависеть от того, как часто целые числа окажутся делимы на 2, 3, 5 и так далее. Эту информацию получить относительно легко. Если же говорить о более сложных схемах, как в случае с простыми-близнецами, то важная информация зачастую относится к остаткам от деления простых на разные числа. Например, как часто деление простого числа на 3 даёт остаток 1? Или остаток 8 при делении на 15?
Углубляясь всё дальше вдоль числовой оси, эти остатки выстраиваются в статистически предсказуемые паттерны. В 1896 году бельгийский математик Шарль Жан де ла Валле-Пуссен доказал, что остатки постепенно выравниваются – например, если помещать простые числа в одну из двух корзин в зависимости от остатка при делении на 3 – 1 или 2 – то в конечном итоге в обеих корзинах окажется примерно равное их количество. Но для того чтобы полностью раскрыть потенциал методов отсеивания, математикам недостаточно знать, что содержимое корзин постепенно выравнивается, им также нужно понимать, каким образом это происходит.
Выяснить же это оказалось непросто. После двух основных прорывов – в 60-х и 80-х – новые исследования в основном затихли. Яркое исключение произошло в 2013 году, когда Итан Чжан опубликовал знаковое доказательство существования бесконечного множества пар простых чисел, которые расположены ближе друг к другу, чем к некой конечной границе. Но в основной работе, производившейся в 80-е годы, в течение более 30 лет ощутимого прогресса не наблюдалось.
Сейчас же эта тема переживает период возрождения, чему способствовала серия из трёх работ, написанных оксфордским математиком Джеймсом Мейнардом в 2020 году (за два года до того, как он получил Филдсовскую премию – высшую награду в сфере математики). Мейнард проанализировал число, называемое «уровнем распределения», которое отражает то, насколько быстро остатки от деления простых чисел достигают равного распределения по корзинам (иногда при использовании конкретных методов отсева). Для многих типичных методов он показал, что уровень распределения равен не менее 0,6, побив предыдущий рекорд в 0,57, установленный в 80-е годы.
«Работа Мейнарда и последующие подогретые ей исследования «вдыхают новую жизнь в аналитическую теорию чисел. – сказал Джон Фридландер из Университета Торонто, который участвовал в изысканиях, производимых в 80-х. – Это реальное возрождение».

Джулия Штадлман, Джаред Дюкер Лихтман и Александру Паскади (слева направо) – все подтвердили новые результаты исследований распределения простых чисел.
В течение нескольких последних месяцев трое бывших студентов Мейнарда опубликовали свои работы (1, 2, 3), расширяющие полученные Мейнардом и Чжаном результаты. Одна из них, написанная Джаредом Дюкером Лихтманом, (сейчас является постдоком в Стэнфордском университете), продвинула установленный Мейнардом уровень распределения до 0,617. Используя этот прирост, Лихтман в последствии вычислил более точные верхние пределы количества простых-близнецов вплоть до установленной конечной точки, а также число «представлений Гольдбаха». — представлений чётных чисел как суммы двух простых.
«Эти молодые умы развивают тему, которая сегодня реально стала актуальной». – сказал Эндрю Гранфилл из Монреальского университета.
Повышение с 0,6 до 0,617 может казаться небольшим для людей, не знакомых с теорией чисел. Но в теории отсева Гранвилл сказал, что «иногда эти скромные победы могут иметь поразительные последствия».
▍ Включение и исключение
Чтобы оценить, сколько чисел исключает отсев вплоть до конечной точки N, математики используют подход, основанный на так называемом включении/исключении. Для его понимания разберём отсев по Эратосфену. Он начинается с удаления всех чисел, кратных 2 – это около половины чисел до N. Далее удаляются все значения, кратные 3 – ещё около 1/3 всех чисел до N.
И здесь вы можете решить, что к этому моменту удалили около 1/2 + 1/3 всех чисел до значения N. Но это завышенное представление, поскольку вы дважды считаете числа, являющиеся кратными 2 и 3 (кратные 6). Они составляют около 1/6 всего диапазона до N, значит, чтобы компенсировать этот двойной подсчёт, нужно вычесть 1/6, получив общую формул 1/2 + 1/3 – 1/6.
Теперь можно переходить к числам, кратным 5 – так мы добавим к общему числу ещё 1/5, но тут придётся вычесть 1/10 и 1/15, чтобы учесть повторы чисел, которые делимы на 2 и 5 или на 3 и 5. И даже на этом ещё не всё – мы случайно дважды учли повторы, которые делимы на 2, 3 и 5. Для исправления этой неточности придётся прибавить к общему числу 1/30, получив формулу 1/2 + 1/3 – 1/6 – 1/10 – 1/15 + 1/30.
По мере продолжения этого процесса в формуле появляется всё больше членов, включая дроби с увеличивающимися знаменателями. Чтобы исключить излишнее нагромождение мелких ошибок в примерных оценках вроде «около 1/2» и «около 1/3», теоретики обычно останавливают процесс сложения и вычитания до прохождения всего отсева и вместо точного ответа ограничиваются верхней и нижней границами.
В теории аналогичный процесс должен работать и для более изощрённых множеств простых чисел вроде простых-близнецов. Но, когда дело доходит до чего-то подобного, включение/исключение не сработает, если вы не будете знать, насколько равномерно остатки от деления распределяются по корзинам.
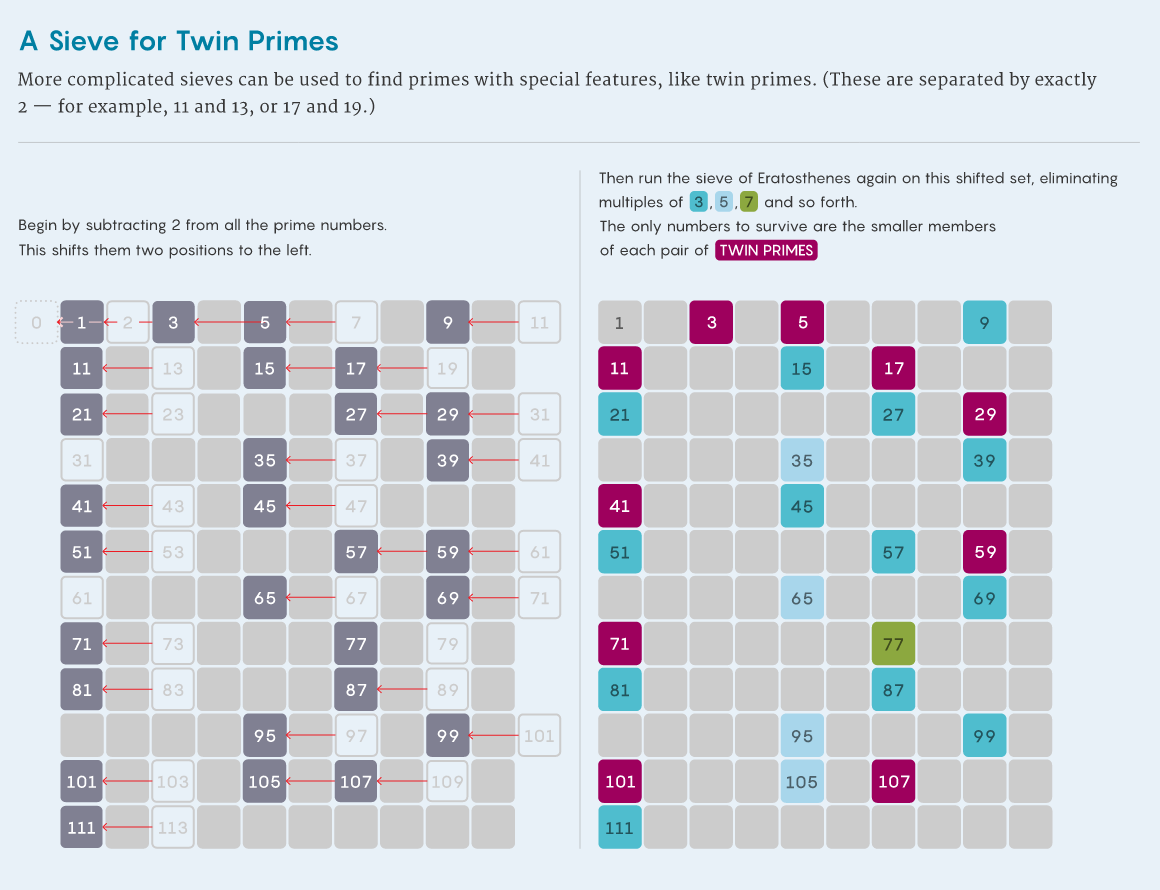
Чтобы это увидеть, подумайте о том, как мог бы работать отсев простых-близнецов. Можете начать с использования метода Эратосфена для поиска всех простых вплоть до значения N. Затем выполните второй круг отсева, удалив все простые, не являющиеся частью пары близнецов. Один из вариантов сделать это – отбрасывать простое, если число, находящееся в двух шагах от него слева, не является тоже простым (можно также анализировать на два шага вправо). Используя отсев по левой стороне, мы сохраним простые вроде 13, поскольку 11 тоже является простым, но вычеркнем такие, как 23, поскольку 21 уже к простым не относится.
Можете рассматривать процесс этого отсева как смещение множества простых на две единицы влево, сопровождаемое вычёркиванием в смещённом множестве всех чисел, не являющихся простыми (например, 21). В смещённом множестве вы вычёркиваете числа, кратные 3, затем кратные 5 и так далее. (Вам не нужно беспокоиться о числах, кратных 2, так как в смещённом множестве все числа, кроме первого, нечётные).
Затем идёт включение/исключение, позволяющее оценить, сколько чисел вы вычеркнули. В отсеве по Эратосфену вычёркивание чисел, кратных 3, ведёт к удалению примерно 1/3 всех чисел. Но в более мелком множестве смещённых простых сложнее спрогнозировать, сколько будет исключено при вычёркивании кратных 3.
Любое число k в смещённом множестве на 2 меньше некоего простого числа. Значит, если k кратно 3, тогда соответствующее ему простое, k + 2, при делении на 3 будет иметь остаток 2. Простые числа при делении на 3 имеют остаток 1 либо 2 (за исключением самой 3). Из этого следует, что половина простых вплоть до N даёт остаток 1, а вторая половина – остаток 2. Это будет означать, что на данном этапе отсева мы вычёркиваем примерно половину чисел смещённого множества (вместо 1/3, как при отсеве по Эратосфену). Значит, в качестве результата формулы подсчёта исключений/включений мы записываем 1/2.
Благодаря де ла Валле-Пуссену, нам известно, что при делении на 3 в конечном итоге половина всех простых даст остаток 1, а вторая половина – остаток 2. Но для выполнения включения/исключения недостаточно знать, что корзины с остатками выравниваются – нужно также знать, что этот баланс устанавливается к моменту достижения N. В противном случае мы не можем быть уверены в том, что сумма по итогу всех включений/исключений составит 1/2. Более ста лет математиков беспокоило, что распределение простых чисел имеет странности, которые исключают некоторые из значений, необходимых для получения результата включений/исключений.
«Если у вас нет теорем распределения, то вы не сможете понять, что происходит, когда вы завершаете отсев». – сказал Теренс Тао из Калифорнийского университета Лос-Анджелеса.
▍ Поворотная точка
Один из вариантов прогнозирования того, насколько быстро корзины начнут выравниваться, был доступен теоретикам в виде самой известной нерешённой задачи в теории чисел – обобщённой гипотезы Римана. Эта гипотеза в случае своей верности подразумевает, что при рассмотрении всех простых в диапазоне до очень большого числа N остатки от их деления равномерно распределяются по корзинам для любого делителя вплоть до примерно квадратного корня из N.
Таким образом, например, если мы рассматриваем простые в диапазоне до 1 триллиона, то будем ожидать равномерное распределение остатков от их деления на 120, 7,352 или 945,328 – любой делитель менее ~1 миллиона (квадратный корень из 1 триллиона).
Математики говорят, что эта гипотеза прогнозирует уровень распределения простых не менее ½, поскольку ещё один способ записать квадратный корень из N – это N1/2.

Джеймс Мейнард и его студенты выясняли, как быстро простые начинают подчиняться статистически прогнозируемым паттернам
Если описанная гипотеза верна, это будет означать, что при отсеве до 1 триллиона вы можете вычёркивать числа, кратные 2, затем кратные 3, потом кратные 5 и продолжать, пока в формуле включения/исключения не начнут появляться делители больше ~1 миллиона. За пределами этой точки вычислять члены формулы уже не получится. В середине XX века теоретики доказали множество теорем отсева, следуя правилу: «Если обобщённая гипотеза Римана верна, то…»
Но для получения многих из этих результатов не требовалась вся суть гипотезы Римана – было достаточно знать, что простые числа успешно распределялись по корзинам почти для каждого делителя, а не для каждого. В середине 60-х Энрико Бомбьери и Аскольд Виноградов по-отдельности (1, 2) смогли доказать это: «Если мы ограничиваемся пониманием, что корзины выравниваются для почти каждого делителя, то уровень распределения простых чисел составляет не менее 1/2».
Теорема Бомбьери-Виноградова, которая получила широкое применение, внезапно подтвердила многие результаты, которые до этого опирались на недоказанную гипотезу Римана. «Она подобна золотому стандарту среди теорем распределения». – сказал Тао.
Но математики давно подозревали, а численные свидетельства предполагали, что истинный уровень распределения простых намного выше. В конце 60-х Питер Эллиот и Хейни Халберстам предположили, что уровень распределения простых лишь немного меньше 1 – иными словами, если рассматривать простые в диапазоне до некоего огромного числа, то они должны равномерно распределяться по корзинам даже при делителях, очень близких к этому огромному числу. И эти большие делители имеют значение при выполнении включения/исключения, поскольку появляются, когда вы делаете поправку на излишний подсчёт. Так что, чем ближе математики могут подобраться к предположенному Эллиотом и Халберстамом уровню распределения, тем большее число членов они смогут вычислить в формуле включений/исключений. Хотя доказательство гипотезы Эллиота-Халберстама, со слов Тао, является «мечтой».
Тем не менее до сих пор никто ещё не смог превзойти уровень распределения 1/2 в полной степени обобщённости, которая достигается с помощью теоремы Бомбьери-Виноградова. Математики начали называть эту загвоздку «барьером квадратного корня» для простых чисел. Этот барьер, как сказал Лихтман, «Является поворотной точкой в нашем понимании простых чисел».
▍ Новые мировые рекорды
Однако во многих задачах отсева можно добиваться успеха даже при ограниченном понимании того, как простые числа распределяются по корзинам. Возьмите, к примеру, задачу простых-близнецов: отсев простого, если число на две единицы влево от него делимо на 3, 5 или 7, равноценно вопросу о том, даст ли само это простое остаток 2 при делении на 3, 5 или 7. Иными словами, попадает ли простое в корзину «2» при любом из этих делителей. Так что вам не обязательно знать, распределяются ли простые равномерно по всем корзинам при этих делителях – достаточно понимать, содержит ли каждая корзина «2» предполагаемое число простых.
В 80-е годы математики начали искать способ доказать теоремы распределения, которые фокусируются на одной конкретной корзине. Эта работа достигла апогея в 1986 году в работе Бомбьери, Фридландера и Хенрика Иванеца, которые показали, что достигли уровня распределения в 4/7 (около 0,57) для одиночных корзин при использовании хоть и не всех видов отсева, но множества из них.
Как и в случае с теоремой Бомбьери-Виноградова, идеи, которые развились в 80-е годы, нашли себе множество применений. Самое примечательное в том, что они позволили математикам значительно продвинуться (1, 2) в понимании Великой теоремы Ферма. Эта теорема утверждает, что уравнение an + bn = cn не имеет решений с простыми числами при любой экспоненте n больше 2. (Это было доказано в 1994 году при помощи техник, не опиравшихся на теоремы распределения). Однако после всплеска 80-х особого прогресса в понимании уровня распределения не наблюдалось несколько десятков лет.

Знаменательное доказательство Итана Чжана, которое он сделал в 2013 году, ограничив величину промежутков между простыми числами, положило начало возрождения в этой сфере математики.
Затем в 2013 году Чжан выяснил, как преодолеть барьер квадратного корня, двигаясь в направлении, отличном от направления Бомбьери, Фридландера и Иванеца. Он использовал старые непопулярные методы из начала 80-х годов, чтобы добиться малейших улучшений достигнутого Бомбьери и Виноградовым уровня распределения 1/2 при отсеивании только с использованием «гладких» чисел, то есть не имеющих больших простых делителей. Это крохотное улучшение позволило Чжану доказать давнее предположение, что по мере продвижения вдоль числовой оси вы продолжаете встречать пары простых, которые находятся ближе друг к другу, чем к некой фиксированной границе. (В последствии Мейнард и Тао каждый по-отдельности привели своё доказательство этой теоремы, используя улучшенный метод отсева вместо улучшенного уровня распределения).
Полученные Чжаном результаты опираются на одну из версий гипотезы Римана, происходящую из мира алгебраической геометрии. При этом работа Бомбьери, Фриландера и Иванеца опиралась на то, что Мейнард описывает как «некую магическую связь» с объектами, называемыми автоморфными формами, имеющими собственную версию гипотезы Римана. Автоморфные формы представляют собой высокосимметричные объекты, которые, как говорит Тао, относятся к «наиболее значимой стороне теории чисел».
Несколько лет назад Мейнард убедился, что можно добиться большего, совместив лежащие в основе этих двух методов идеи. В своей серии из трёх работ 2020 года, которые Гранвилл назвал «tour de force» (проявление силы), Мейнард смог поднять уровень распределения до 3/5, или 0,6 в чуть более узком контексте, чем тот, что изучали Бомбьери, Фриландер и Иванец.
Сейчас же студенты Мейнарда ещё больше развивают эти техники. Недавно Лихтман обнаружил, как расширить достигнутый Мейнардом уровень до примерно 0,617. Затем он ловко использовал этот прирост при определении новых верхних границ количеств как простых-близнецов, так и представлений Гольдбаха. В случае последних это был первый раз, когда кто-либо смог использовать уровень распределения выше 1/2 из классической теоремы Бомбьери-Виноградова.
Другой студент Мейнарда, Александру Паскади, достиг уровня распределения в 0,617, но не для простых, а для гладких чисел. Гладкие числа возникают в теории чисел аналогично простым, и получаемые в их отношении уровни распределения зачастую совпадают с уровнями распределения простых.
Тем временем третий студент, Джулия Стадлманн, увеличила уровень распределения простых в сеттинге, использованном Чжаном, когда гладкие числа выступают делителями (а не делимыми). Чжан почти преодолел барьер квадратного корня в этом контексте, достигнув уровня распределения в 0,5017, после чего онлайн-коллаборация под именем проект Polymath смогла увеличить это число до 0,5233. Теперь же Стадлманн удалость поднять его до 0,525.
Тао говорит, что другие математики посмеиваются над своими коллегами, занимающимися аналитической теорией чисел, ввиду их одержимости даже незначительными продвижениями в численных показателях. Но эти крохотные улучшения важны за пределами рассматриваемых чисел.
«Это можно сравнить с бегом на 100 метров, когда финишируешь на сотые доли секунды быстрее. Каждый новый мировой рекорд отражает то, насколько далеко продвинулись твои методы.
В целом техники становятся всё более ясными и унифицированными. Как только ты продвигаешься в одной задаче, становится понятно, как применить это к другой». – сказал он.
«Пока ещё для всех этих научных достижений нет какого-то значительного применения, но сама эта новая работа меняет наше . И это не просто что-то вроде забить гвоздь посильнее – скорее, создание более совершенного молотка». – сказал Гранвилл.
Автор: Дмитрий Брайт