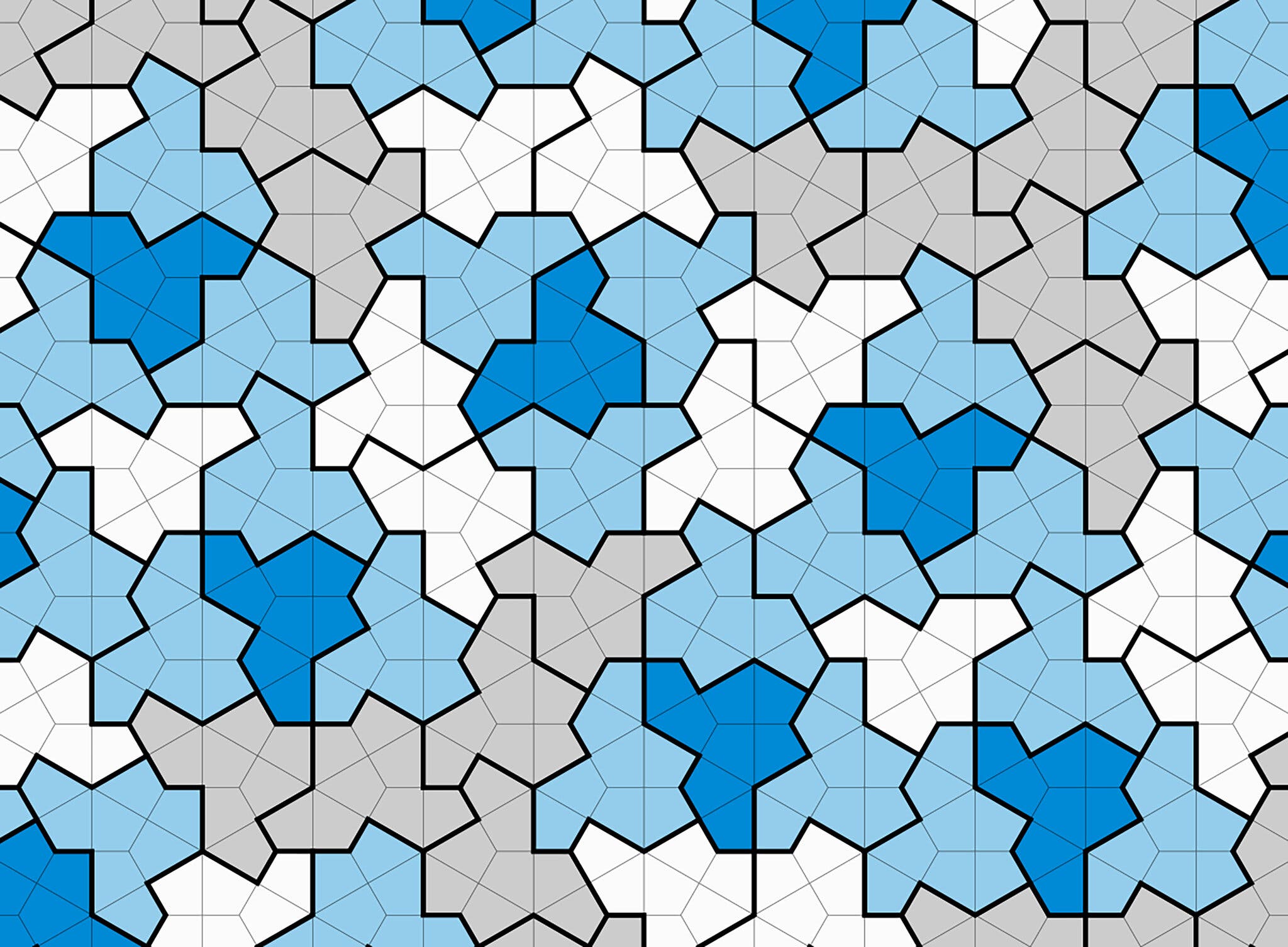
В ноябре прошлого года, после десяти лет неудачных попыток, Дэвид Смит, самопровозглашенный «любитель фигур» из Бридлингтона в Восточном Йоркшире, Англия, заподозрил, что, возможно, он наконец-то решил давнюю задачку в математике замощения плоскости: иначе говоря, он решил, что нашёл «эйнштейна».
В менее поэтичных терминах, «эйнштейн» — это «апериодическая моноплитка», фигура, которая покрывает плоскость или бесконечную двумерную плоскую поверхность неповторяющимся образом. (Термин «эйнштейн» происходит от немецкого «ein stein» или «один камень», в более свободной трактовке — «одна плитка» или «одна фигура»). Ваши обычные обои или кафельный пол представляют собою часть бесконечного узора, который периодически повторяется; при смещении или «переносе» узор может быть точно наложен сам на себя. Апериодическая плитка не обладает такой «трансляционной симметрией», и математики давно ищут единственную фигуру, которая могла бы покрыть плоскость такой плиткой. Эта задача известна под названием «проблемы Эйнштейна».
«Я всегда любил возиться и экспериментировать с фигурами», — сказал 64-летний Смит, который, помимо прочей работы, работал техником в типографии и рано вышел на пенсию. Хотя ему нравилась математика в средней школе, он не преуспел в ней, сказал он. Но его давно «навязчиво занимала» проблема Эйнштейна.
И вот теперь новая статья, написанная Смитом с тремя соавторами, обладающими математическим и вычислительным опытом, доказывает истинность открытия Смита. Исследователи назвали свою эйнштейновскую фигуру «шляпой», поскольку она напоминает фетровую шляпу. (Сам Смит часто повязывает на голову бандану). Работа ещё не прошла рецензирование.
«Это, похоже, замечательное открытие!» — написал в электронном письме Джошуа Соколар, физик из Университета Дьюка, который ознакомился с ранней копией статьи, предоставленной «Нью-Йорк Таймс». «Наиболее важным аспектом для меня является то, что плитка явно не попадает ни в один из известных нам классов структур».
«Математический результат порождает некоторые интересные вопросы физики, — добавил он. — Можно представить себе открытие или изготовление материала с такой внутренней структурой». Д-р Соколар и Джоан Тейлор, независимый исследователь из Берни, Тасмания, ранее обнаружили шестиугольную моноплитку, состоящую из несоединенных друг с другом частей, что, по мнению некоторых, нарушает условия задачи. (Они также нашли связную трёхмерную версию плитки Соколара-Тейлора).

Эксперимент Дэвида Смита с использованием фигур, вырезанных из бумаги.
От 20 426 до одного
Изначально стремление к математическому замощению плоскости было мотивировано довольно общим вопросом: существует ли набор фигур, которые могут покрывать плоскость только непериодически? В 1961 году математик Хао Ванг предположил, что такие наборы невозможны, но его ученик Роберт Бергер вскоре доказал, что предположение неверно. Доктор Бергер обнаружил апериодический набор из 20 426 плиток, а затем и набор из 104 плиток.
Тогда игра немного поменялась: какого минимального количества плиток будет достаточно для этого? В 1970-х годах сэр Роджер Пенроуз, физик-математик из Оксфордского университета, получивший в 2020 году Нобелевскую премию по физике за исследование чёрных дыр, довёл это число до двух.
С тех пор другие исследователи придумывали формы этих двух плиток. «У меня тоже есть пара-тройка своих», — сказал Хаим Гудман-Стросс, ещё один из авторов статьи, профессор Университета Арканзаса, который также занимает должность математика-просветителя в Национальном музее математики в Нью-Йорке.

Пример плитки Пенроуза с воздушными змеями и дротиками.
Он отметил, что чёрные и белые квадраты также могут создавать странные непериодические узоры в дополнение к привычному периодическому шашечному узору. «На самом деле уметь создавать странные и интересные узоры довольно просто, — сказал он». Магия двух плиток Пенроуза заключается в том, что они создают только непериодические узоры — это все, что они могут делать.
«И тогда Святой Грааль превратился в следующий вопрос: можно ли обойтись одной плиткой?» — сказал доктор Гудман-Стросс.
Ещё несколько лет назад сэр Роджер стремился к эйнштейну, но он отложил эти поиски в сторону. «Я сократил число до двух, а теперь мы сократили его до одного! — сказал он о шляпе. — Это просто чудо. Я не вижу причин не верить в это».
В статье приводится два доказательства, оба выполненные Джозефом Майерсом, соавтором и разработчиком программного обеспечения из Кембриджа, Англия. Одно из них было традиционным доказательством, основанным на предыдущем методе, с добавлением специально написанного кода; другое использовало новую технику, не компьютерную, разработанную доктором Майерсом.
Сэр Роджер счёл доказательства «очень сложными». Тем не менее, он был «чрезвычайно заинтригован» эйнштейном. Он сказал: «Это действительно хорошая фигура, поразительно простая».
Творческий мастер
Простота фигуры была найдена честным путём. Смит проводил свои исследования в основном вручную; один из его соавторов назвал его «творческим мастером».

Замощение плоскости «шляпой» Смита, сделанное с помощью программы Polyform Puzzle Solver Яапа Шерпхуиса.
Сначала он всегда прикидывал возможности на экране компьютера при помощи программы PolyForm Puzzle Solver, разработанной Яапом Шерпхуисом, ещё одним любителем плиток и теоретиком головоломок из Делфта, Нидерланды. Но если у фигуры открывался потенциал, Смит использовал резальную машину Silhouette, чтобы изготовить партию из 32 картонных копий плитки. Затем он собирал плитки вместе, без зазоров и накладок, как головоломку, поворачивая и переворачивая плитки по мере необходимости.
«Всегда приятно работать руками, — сказал Смит. — Это может быть очень медитативным занятием. И этот процесс помогает лучше понять, укладывается ли фигура в мозаику или нет».
Когда в ноябре он нашёл плитку, которая, казалось, заполняла плоскость без повторяющегося рисунка, он написал Крейгу Каплану, соавтору работы и компьютерному учёному из Университета Ватерлоо.
«Может ли эта фигура быть решением так называемой «проблемы Эйнштейна» – и в таком случае разве это не круто?» — написал Смит.
«Было ясно, что в этой фигуре есть что-то необычное», — сказал доктор Каплан. Используя вычислительный подход, основанный на предыдущих исследованиях, его алгоритм создавал все большие и большие участки плиток-шляп. «Казалось, что нет предела тому, насколько большую группу плиток может создать программа», — сказал он.
Имея эти исходные данные, Смит и д-р Каплан изучили иерархическую структуру узора из плиток на глаз. Доктор Каплан обнаружил признаки, которые открыли путь к традиционному доказательству апериодичности — метод, который математики «достают из ящика, когда у вас есть набор апериодических плиток», — сказал он.
Первым шагом, сказал доктор Каплан, было «определение набора из четырёх «метатипов», простых фигур, которые обозначают небольшие группы из одной, двух или четырёх шляп». Метатипы собираются в четыре большие фигуры, которые ведут себя аналогично. Эта сборка, от метатипов к супертипам и суперсупертипам, ad infinitum, покрывает «всё большие и большие математические «этажи» с копиями шляпы», — сказал д-р Каплан. «Затем мы показали, что такая иерархическая сборка — это, по сути, единственный способ покрыть плоскость шляпами, чего оказывается достаточно, чтобы показать, что её никогда не получится покрыть плиткой периодически».
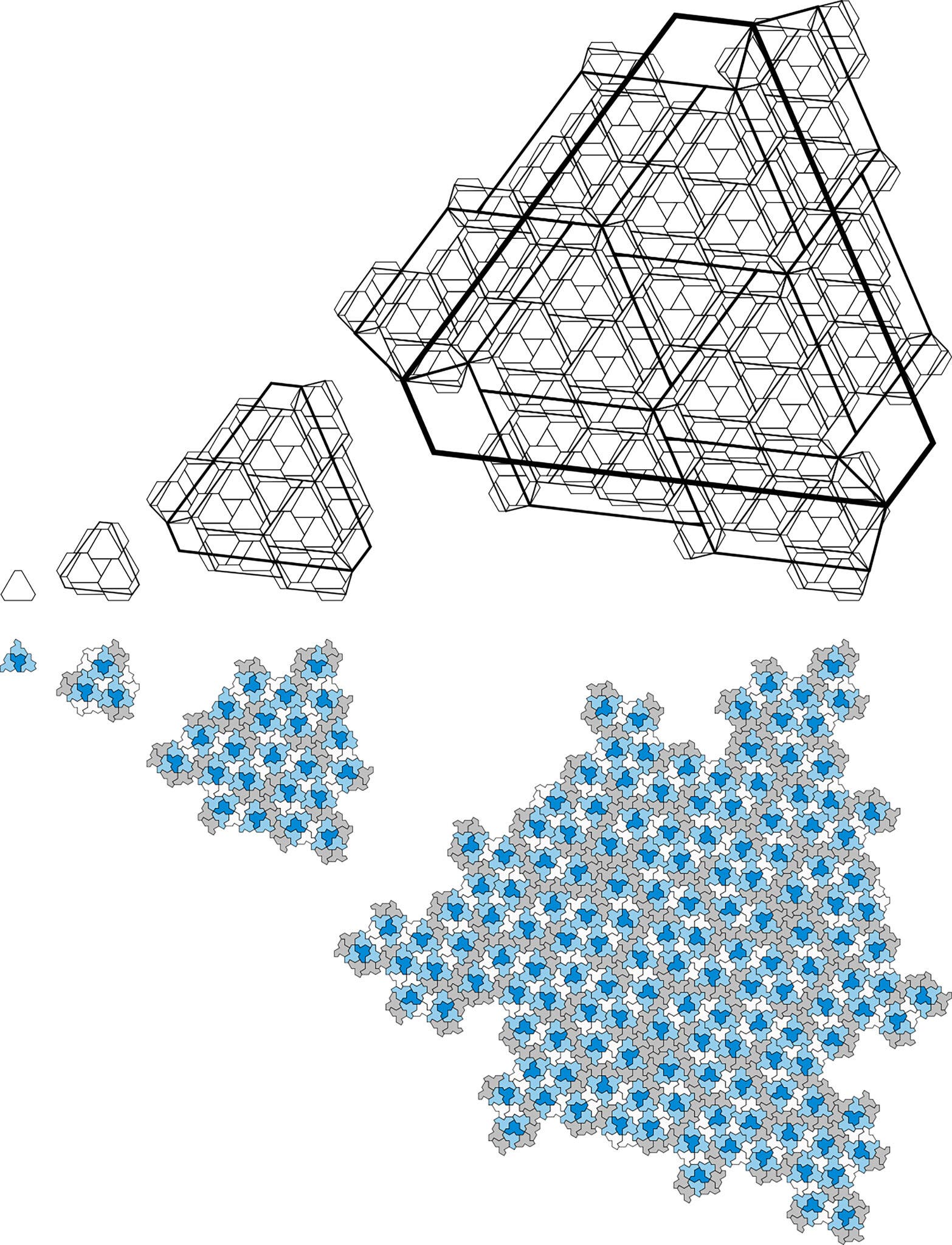
Первые четыре итерации метатипа и его супертипов.
«Это очень умно», — сказал в интервью доктор Бергер, инженер-электрик на пенсии из Лексингтона, штат Массачусетс. Рискуя показаться придирчивым, он отметил, что поскольку в шляпной плитке используются отражения — плитка в фигуре шляпы и её зеркальное отражение — некоторые могут задаться вопросом, не является ли это двухплиточным, а не одноплиточным набором апериодических моноплиток.
Доктор Гудман-Стросс затронул эту тонкость в списке рассылки по тайлингу: «Здесь одна шляпа или две?». Консенсус был таков, что моноплитка считается таковой даже при использовании её отражения. Это оставляет вопрос открытым, сказал доктор Бергер: Существует ли эйнштейн, который способен проделать эту работу без отражения?
Прятки в шестиугольниках
Доктор Каплан пояснил, что «шляпа» не является новым геометрическим изобретением. Это поликайт [kyte (англ.) – воздушный змей, а также четырёхугольник характерной формы / прим. перев.] — он состоит из восьми воздушных змеев. (Возьмите шестиугольник и проведите три линии, соединяющие центр каждой стороны с центром противоположной стороны; шесть фигур, которые получатся в результате, и будут воздушными змеями).
«Вполне вероятно, что другие люди и раньше задумывались об этой фигуре шляпы, но не в таком контексте, чтобы исследовать её плиточные свойства, — говорит доктор Каплан. — Мне нравится думать, что она пряталась на видном месте».
Марджори Сенешаль, математик из колледжа Смита, говорит: «В определённом смысле, она все это время сидела здесь и ждала, пока кто-нибудь её найдёт». Исследования доктора Сенешаля исследуют соседнюю область математической кристаллографии и связи с квазикристаллами.
«Больше всего меня поражает то, что эта апериодическая плитка уложена на шестиугольную решётку, которая является настолько периодической, насколько это вообще возможно», — говорит Дорис Шаттшнайдер, математик из Моравского университета, чьи исследования посвящены математическому анализу периодических плиток, особенно работ голландского художника М.К. Эшера.
Доктор Сенешаль согласилась. «Она сидит прямо в шестиугольниках, — сказала она. — Сколько людей по всему миру будут корить себя за то, что не заметили этого».
Семейство эйнштейнов
Невероятно, но позже Смит обнаружил второго эйнштейна. Он назвал его «черепахой» — поликайтом, состоящим не из восьми, а из 10 воздушных змеев. Это было «сверхъестественно», — сказал доктор Каплан. Он вспоминает, что почувствовал настоящую панику в связи с тем, что уже «утонул в этих шляпах».
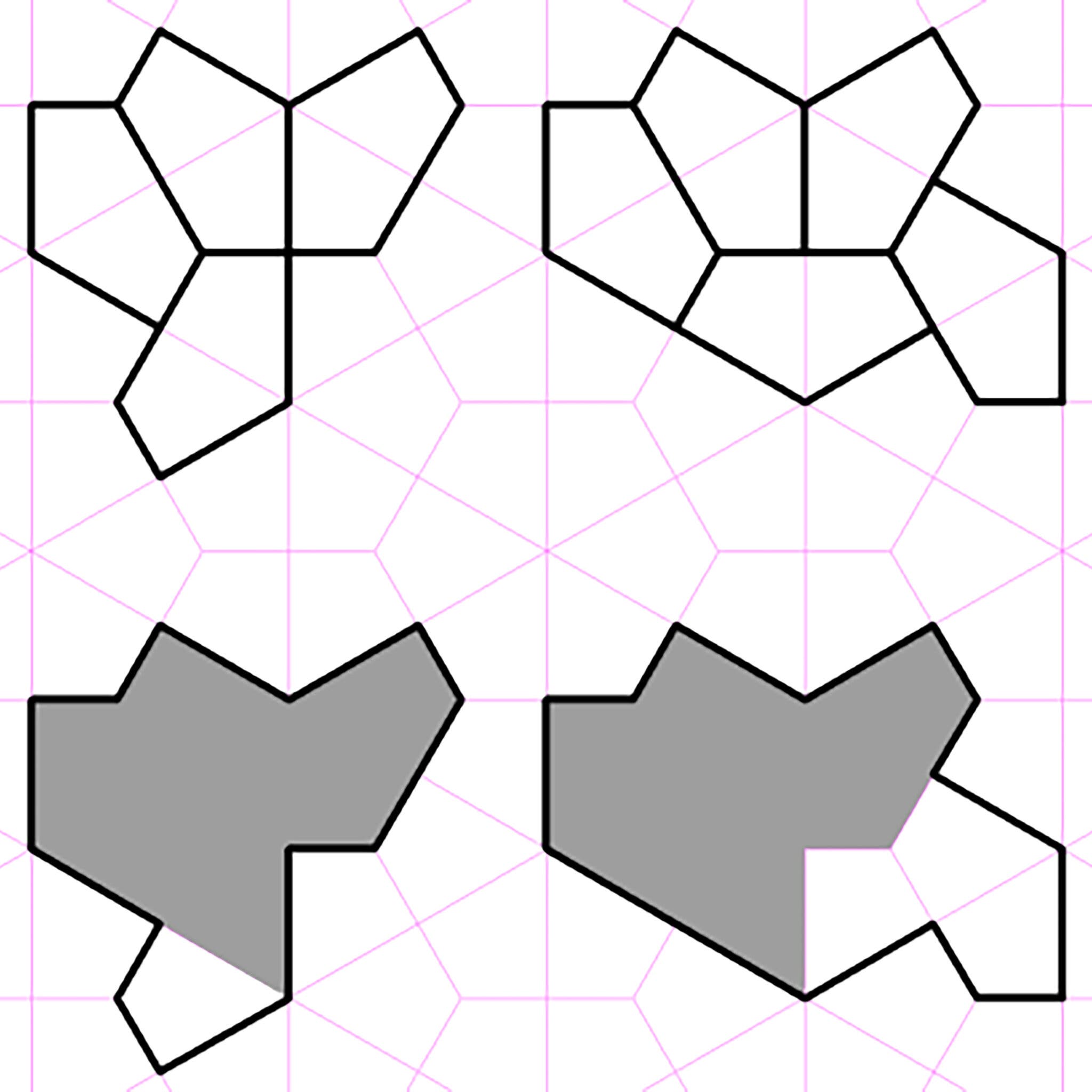
Шляпа (слева) и черепаха.
Но доктор Майерс, который уже проводил подобные вычисления, быстро обнаружил глубокую связь между шляпой и черепахой. И он обнаружил, что на самом деле существует целое семейство родственных эйнштейнов — непрерывная, неисчислимая бесконечность фигур, переходящих одна в другую.
Некоторые другие члены семейства не произвели на Смита такого впечатления. «Они выглядели как самозванцы или мутанты», — сказал он.
Но это семейство эйнштейнов послужило мотивом для второго доказательства, которое предлагает новый инструмент для доказательства апериодичности. Математика казалась «слишком хорошей, чтобы быть правдой», — сказал доктор Майерс в электронном письме. «Я не ожидал другого подобного подхода к доказательству апериодичности — но все сходилось, пока я записал детали».
Доктор Гудман-Стросс считает новую методику важнейшим аспектом открытия; до сих пор существовало лишь несколько доказательств апериодичности. Он признал, что этот метод, возможно, слишком специфичный и подходит только для завзятых ценителей. На обработку математики у него ушло несколько дней. «Потом меня как громом поразило», — сказал он.
Смит был поражён, увидев весь этот процесс подготовки исследовательской работы. «Честно говоря, от меня было мало толку». По его словам, он высоко оценил иллюстрации к работе: «Мне лично больше нравятся картинки».
Автор: Вячеслав Голованов






