Приветствую Вас, уважаемые Читатели! Сегодня я хочу рассказать Вам о замечательном популяризаторе математики Чарльзе Говарде Хинтоне - человеке, внесшем просто огромный вклад в дело изучения объектов четырехмерного мира.
Зачем, спрашивается, их изучать? Я, для начала, ограничусь цитатой его тезки Говарда Лавкрафта, произведения которого я не так давно очень полюбил:

Что знаем мы об этом мире и о Вселенной? — говорил он. — У нас до абсурдного мало органов чувств, а наши представления об окружающих предметах до невероятного скудны. Мы видим вещи такими, какими мы созданы их видеть, и мы не в состоянии постичь абсолютную их суть. Со своими пятью жалкими чувствами мы лишь обманываем себя, иллюзорно представляя, будто воспринимаем весь безгранично сложный космос - "Из глубин мироздания (1934)".
Говард Хинтон - человек с удивительно интересной биографией, но главной заслугой всей его жизни был цикл книг, посвященных пространству. Начиная с простых примеров на прямой и плоскости, Хинтон уводит читателя к объектам трехмерным, а уже затем "подкидывает" нас уже отработанными методами в мир четырехмерный.

В течение своей жизни Хинтон разрабатывал оригинальные методы, с помощью которых не только профессиональные математики, но и любой среднестатистический человек из числа растущих рядов его последователей мог бы «увидеть» четырехмерные объекты. Наконец Хинтон усовершенствовал специальные кубы, которые при условии приложения достаточных стараний помогали визуализировать гиперкубы, или кубы в четырех измерениях.

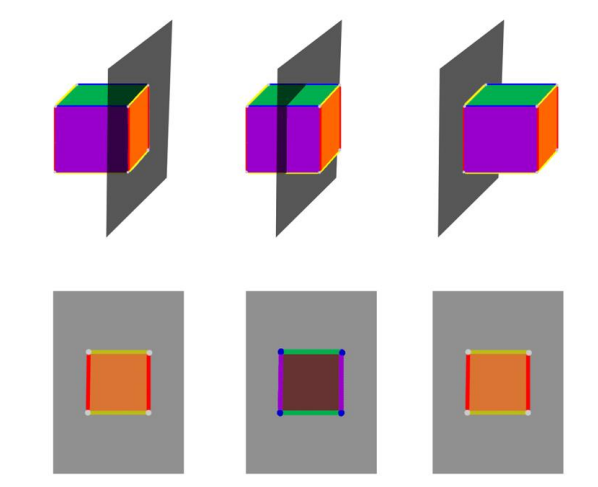
Они получили название «кубы Хинтона». Хинтон даже ввел в обращение официальное название развертки гиперкуба — тессеракт, которое прижилось в английском языке. Давайте рассмотрим подробнее, что же придумал математик. Одним из способов визуализации объектов высших измерений является их пересечение с объектами с меньшей размерностью. Например, возьмем трехмерный куб и пропустим его через двумерную плоскость:

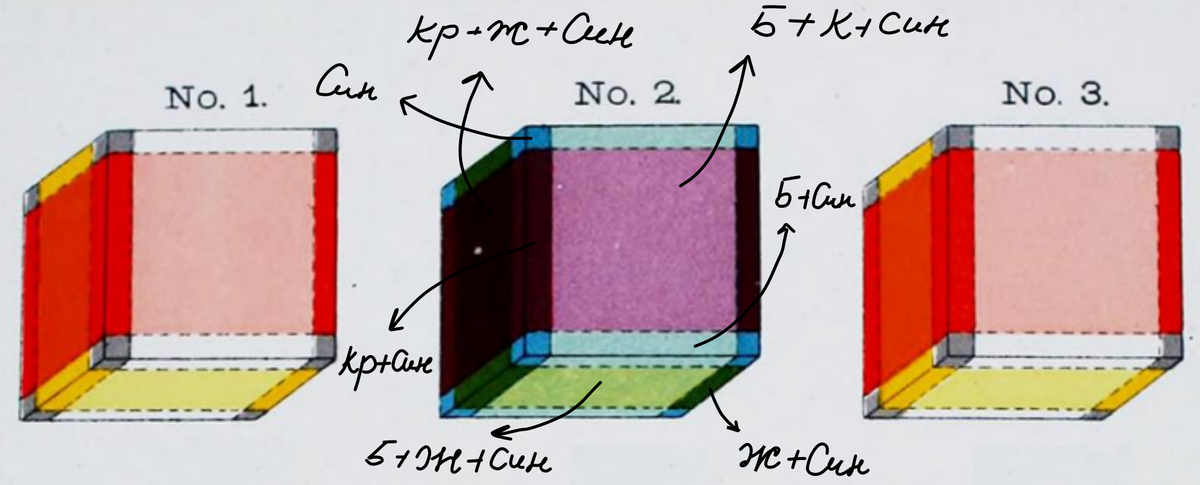
Очевидно, что мы увидим одну из граней куба, а за три прохода - сможем рассмотреть их все, если до этого каким-то образом пометим каждую грань. Именно такой ход и задумывает Хинтон, чтобы визуализировать тессеракт. Если гиперкуб проходит через наше трехмерное пространство, мы могли бы воспринять его трехмерное сечение. Окраска кубиков Хинтона основана на сопоставлении четырех измерений с четырьмя цветами: красным, желтым, синим и белым. Когда точка тессеракта перемещается по измерению, цвет этого измерения добавляется к исходному цвету точки. Конечный цвет - это результат смешивания. Это смешение дает в общей сложности шестнадцать цветов:

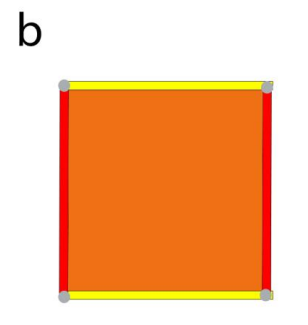
Теперь проследим путь какой-либо точки гиперкуба, чтобы понять принцип формирования цветов его граней. Предположим, что у нас есть точка "без цвета", которая перемещается в пределах желтого измерения x. Результатом будет отрезок линии желтого цвета. Давайте предположим, что эта движущаяся точка начинается и заканчивается начальным цветом и что внутренние точки окрашены в цвет измерения. Таким образом, у нас есть отрезок линии, имеющий конечные точки "нулевого цвета" и желтые внутренние точки:

Отрезок будет перемещаться в пределах "красного" перпендикулярного измерения y. Конечные и начальные точки исходного отрезка будут двигаться в это измерении, оставляя красный след, а грань получившегося квадрата станет желтый+красный = оранжевой!
Теперь переместим этот квадрат в третьем измерении z, которое обозначается синим цветом:
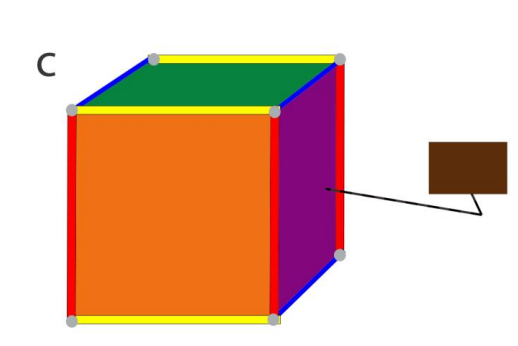
-
Верхняя грань: синий+желтый = зеленый;
-
Грань справа: красный + синий = фиолетовый;
-
Внутренние грани: красный + желтый + синий = коричневый (в соответствии с измерениями, в которых мы двигали наши фигуры!)
Собрав воедино все возможные движения таких точек, можно построить следующую диаграмму:
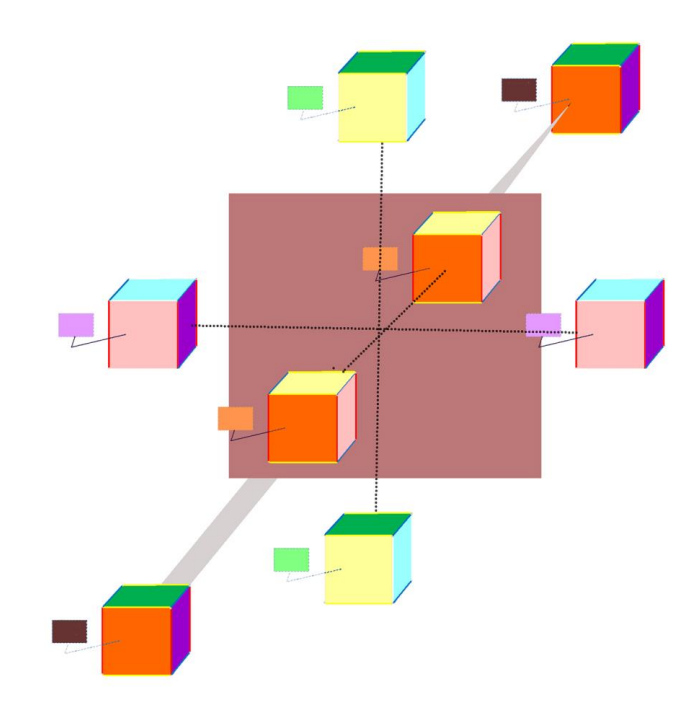
Теперь осталось реализовать приемы пересечения с объектами низших измерений. Пропуская кубы Хинтона через плоскость мы получим, например:
Но наиболее интересной будет визуализация самого гиперкуба. У нас будет четыре варианта, в которых гиперкуб проходит через наше пространство, начиная с одной кубической грани куба Хинтона и заканчивая противоположной (аналогично окрашенной) гранью, а все грани будут иметь дополнительный цвет в зависимости от измерения, отсутствующего в трехмерном пространстве:
-
Если куб имеет желтые, белые и красные грани, будет добавлен синий цвет.
-
Если куб имеет желтые, синие и красные грани, будет добавлен белый цвет.
-
Если он имеет синие, красные и белые грани, то будет добавлен желтый цвет.
-
Если он имеет желтые, белые и синие грани, то будет добавлен красный цвет.
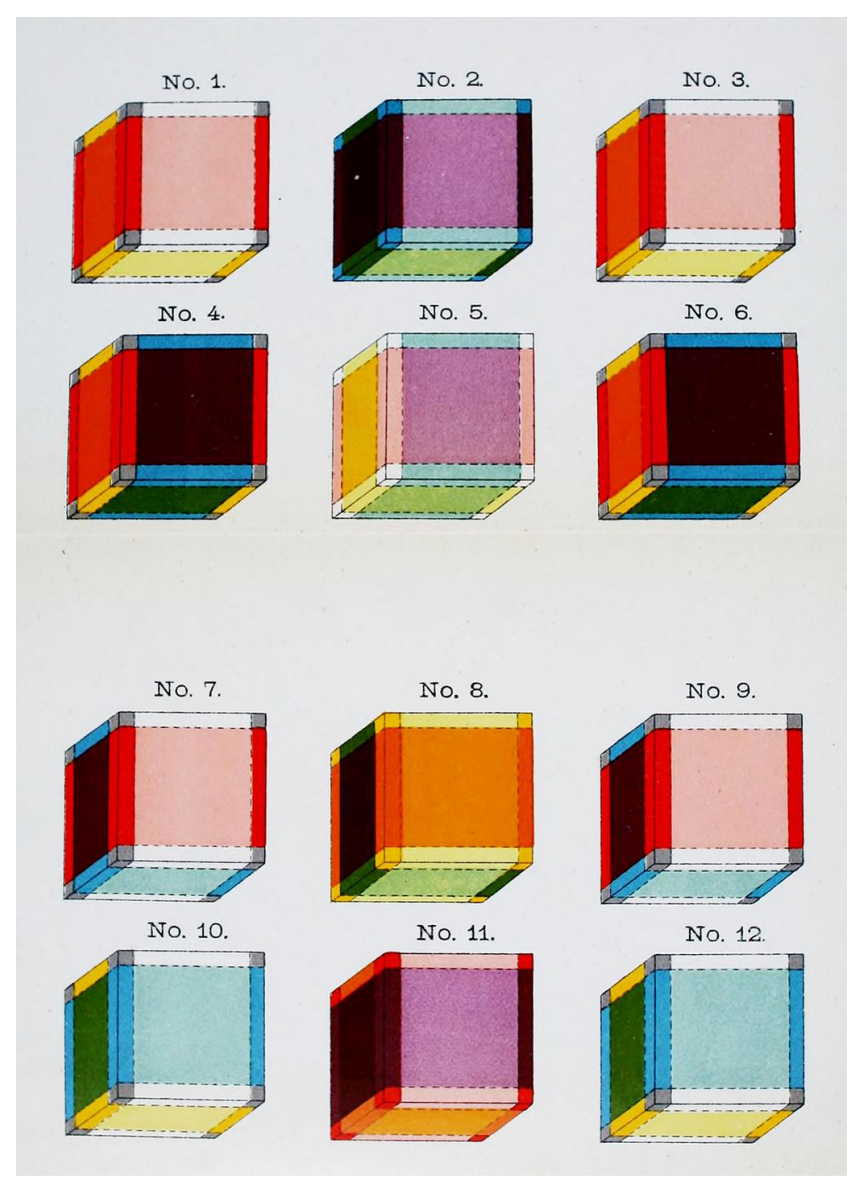
Разберем для примера первую строку: 1. Точка без цвета двигается вправо в белом измерении - получаем белый отрезок. 2. Отрезок движется в красном измерении - получаем квадрат с розовой гранью (белый + красный). 3. Квадрат движется в желтом измерении - получаем куб. 4. Теперь устремляем гиперкуб в четвертом измерении (а это отсутствующий синий цвет!)
На выходе гиперкуб "выворачивается" к нам первоначальной стороной. На самом деле изготовить кубики Хинтона и "поиграться в натуре" можно и самому, затратив на это некоторые усилия:

Кубы Хинтона широко рекламировались в женских журналах и даже применялись на спиритических сеансах, где вскоре приобрели мистическое значение. Представители высшего общества утверждали: медитируя на кубах Хинтона, можно уловить проблески четвертого измерения, а значит, и потустороннего мира духов и умерших близких. Его ученики часами изучали эти кубы, медитировали на них, пока не приобретали умение мысленно переставлять и разбирать эти кубы посредством четвертого измерения, получая гиперкуб. Высказывалось утверждение, будто бы тот, кто справляется с этой умственной задачей, способен достичь высшего состояния — нирваны.

Сам Хинтон после публикации материалов о четвертом измерении жил довольно размеренной и успешной жизнью, пока не был арестован (внезапно, отец Хинтона, Джеймс Хинтон, был хирургом и сторонником полигамии) за двоеженство и был вынужден отправиться в Японию, где работал учителем. Переехав через несколько лет в Северную Америку, Говард работал во многих университетах и всё так же увлеченно рассказывал научному сообществу и простым гражданам о четвертом измерении.

Надо сказать, довольно успешно. Например, в романе Герберта Уэллса «Машина времени» (1895) Путешественник рассуждает о природе четвёртого измерения прямым текстом из рассказа «Незавершённая связь» второго сборника Хинтона (1895). Великий Хорхе Луис Борхес вообще включил произведения Хинтона в свою "вавилонскую библиотеку" и несколько раз упоминал англичанина в своих коротких, но глубоких рассказах. Ушел в "четвертое измерение" Хинтон внезапно - от кровоизлияния в . За ним, чуть меньше, чем через год последовала супруга, наложив на себя руки. Через год после их смерти в 1908 году немец Герман Минковский впервые математически строго определит четырехмерное пространство-время...впрочем, это уже совсем другая история.
Больше математики в Telegram - "Математика не для всех"
Автор:
andreybrylb