Как им это удалось?

Расшифровка таблички
Для начала расшифруем саму табличку. Она маркирована как YBC 7289 (сокращённо от «7289-й предмет из Вавилонской коллекции Йеля, Yale Babylonian Collection»). На табличке показан квадрат, его диагональ, а рядом написаны числа. Вот её стилизованная версия из книги Episodes from the Early History of Mathematics Асгера Обое.
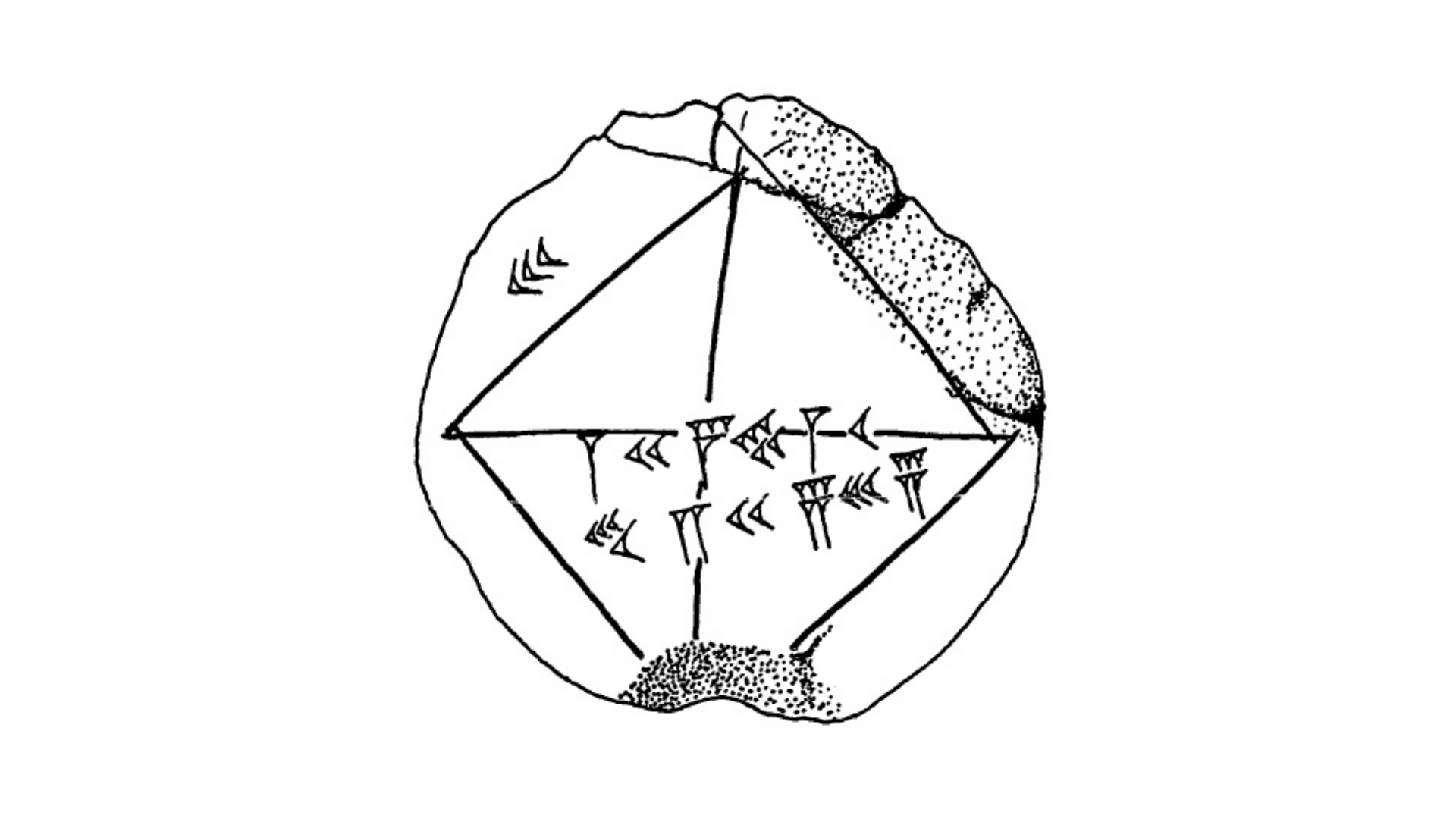
Как следует из теоремы Пифагора, длина диагонали единичного квадрата равна √2. Давайте разберёмся с символами!
На табличке указаны числа, записанные в виде вавилонских клинописных нумералов. Они означают 1, 24, 51 и 10.
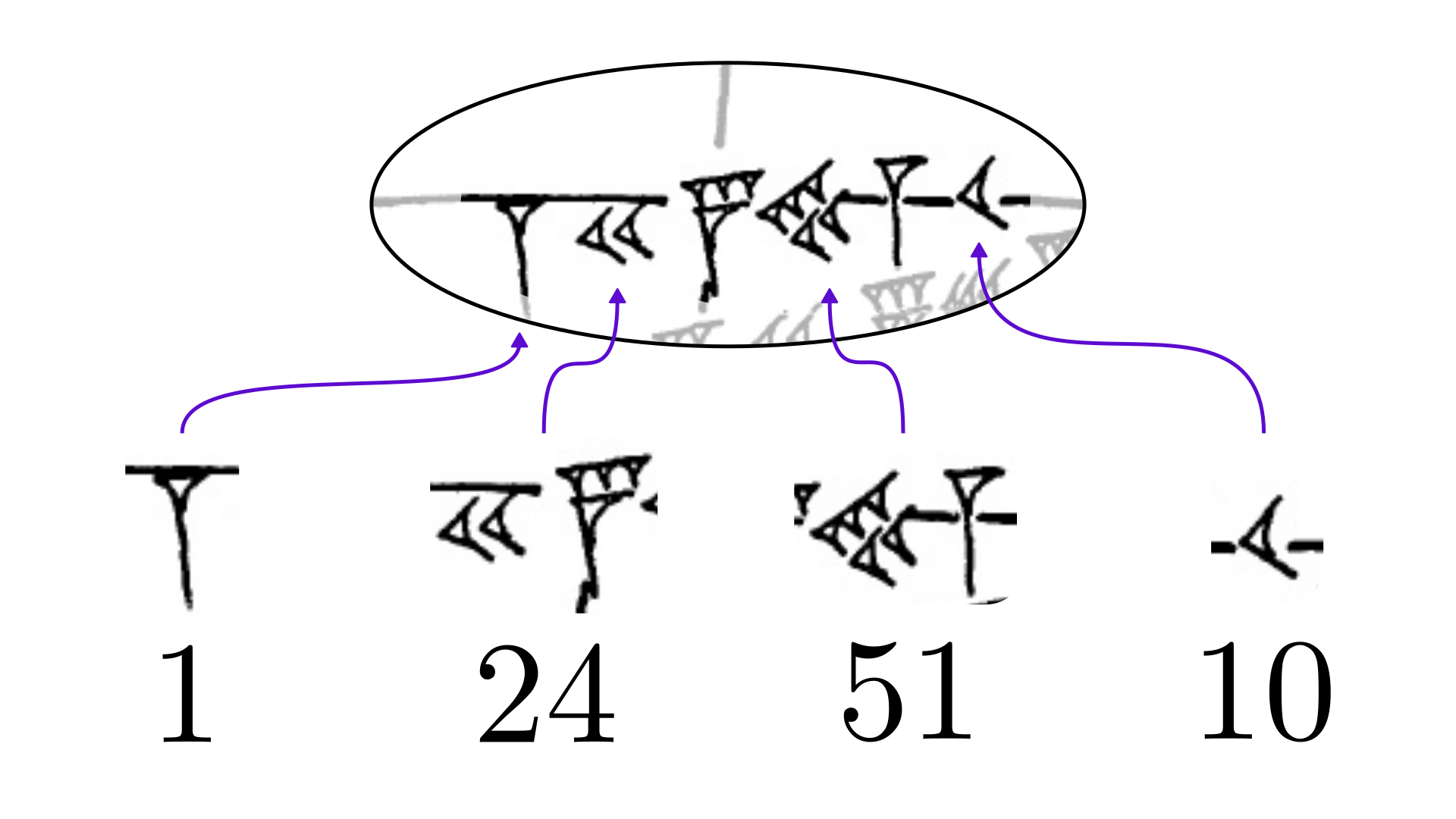
Так как вавилоняне использовали систему счисления по основанию 60 (также называющуюся шестидесятеричной), число 1,24 51 10 в десятичной системе означает 1,41421296296.
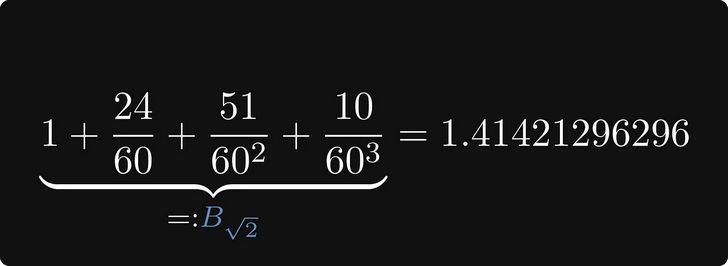
Это совпадает со значением √2 до шестого знака после запятой, то есть соответствует точности в 99,9999%!

Точность вычислений поражает. Попробуйте воссоздать её без калькулятора, на бумаге, это не так уж просто!
И мы расскажем, как им это удалось.
Вавилонский алгоритм вычисления квадратного корня
Сейчас я буду изображать фокусника: сначала покажу алгоритм, а затем отдёрну занавес и объясню его.
Мы начинаем с выбора числа x₀ между 1 и √2. Я знаю, это кажется случайным, но не будем торопиться. Например, таким числом может быть 1,2, что станет нашей первой аппроксимацией.
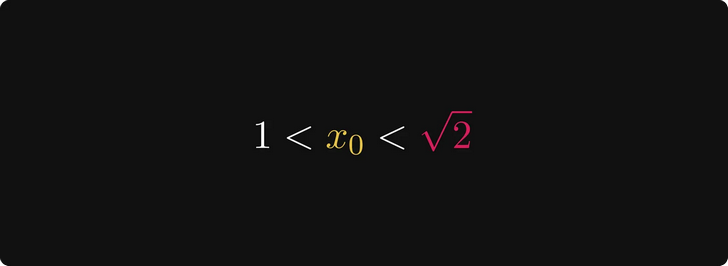
Исходя из этого, 2/x₀ больше √2.
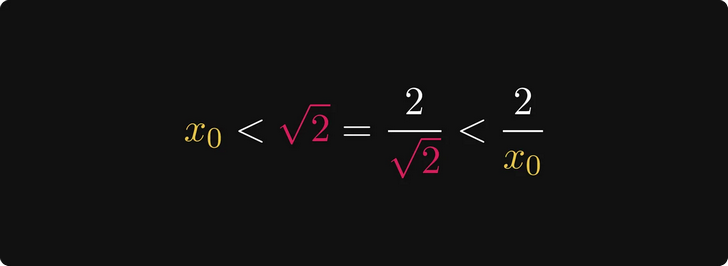
Следовательно, интервал [x₀, 2/x₀] включает в себя √2.
Из этого следует, что средняя точка интервала [x₀, 2/x₀] является более точной аппроксимацией значения √2. Как видно на рисунке ниже, она существенно лучше!
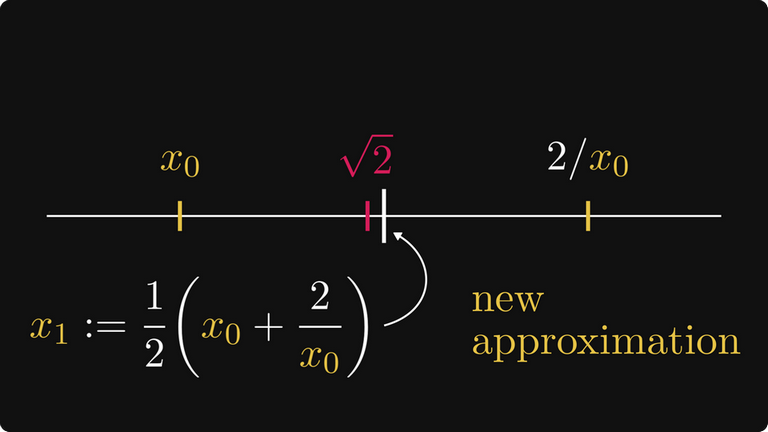
Давайте определим из этого x₁.
Развивая эту тему, мы можем определить последовательность аппроксимации, беря средние точки таких интервалов.
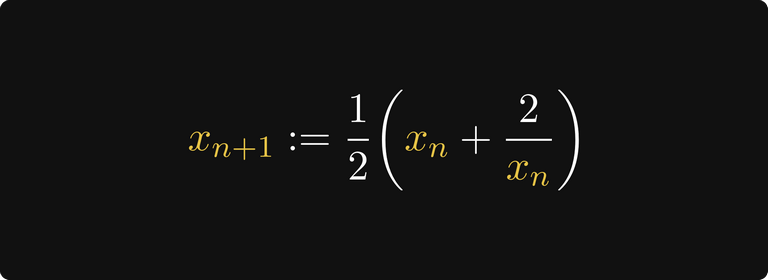
Вот несколько первых членов последовательности. Даже третий член уже является на удивление хорошей аппроксимацией.

Если мы нанесём эти числа на диаграмму рассеяния, то спустя несколько шагов нам уже практически понадобится микроскоп, чтобы увидеть отличия от √2.

Как видите, это сходится к √2 чрезвычайно быстро.
Но насколько быстро?
Погрешность вавилонской аппроксимации
Погрешность между этой аппроксимацией и значением √2 определяется просто как расстояние между ними, замеренное по абсолютному значению их разности. Например, погрешность нашего первого предположения e₀ задаётся следующим образом:
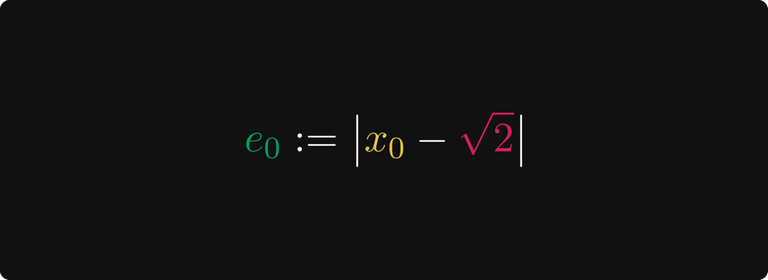
Каким бы малым или большим ни было e₀, мы можем использовать её для оценки последующих погрешностей.
Давайте займёмся алгеброй и посмотрим, как e₀ относится к e₁! Сначала выразим e₁ в виде дроби.
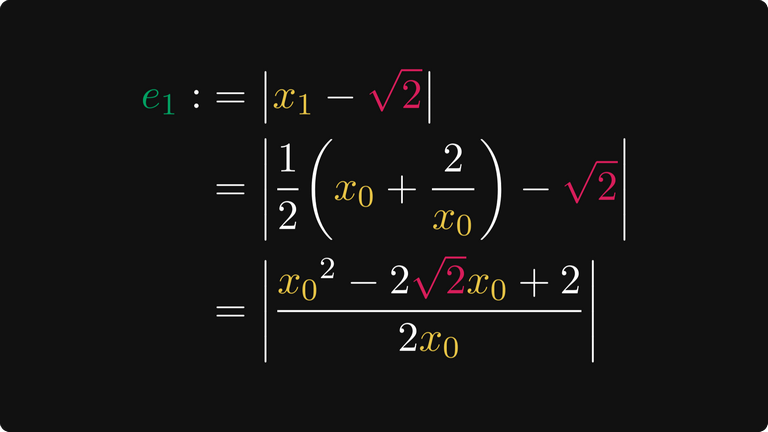
Тогда поскольку мы выбрали x₀ больше единицы, то можем выразить его в членах e₁. Так как числитель e₀ возведён в квадрат, наша задача проста.
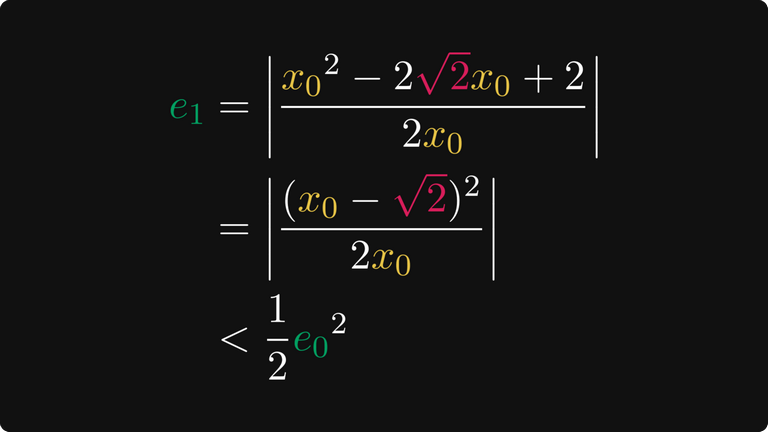
Повторяя эти рассуждения, мы получаем, что сходимость очень быстра, даже быстрее экспоненциальной!
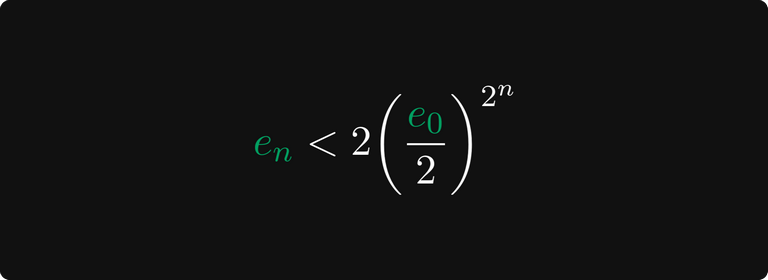
Повезло ли вавилонянам, или они угодили в самую точку?
На самом деле, второе. Настало время поднять занавес!
Метод Ньютона-Рафсона
Давайте перефразируем задачу аппроксимации квадратного корня из двух. Вместо того, чтобы вычислять функцию f(x) = √x в заданной точке, попробуем найти корень (положительный) f(x) = x² — 2. (Который, как оказывается, тоже равен √2.)
Существует ли обобщённый метод решения такой задачи? Да, это метод Ньютона-Рафсона. Чтобы показать, как он работает, давайте приблизим корень f(x).
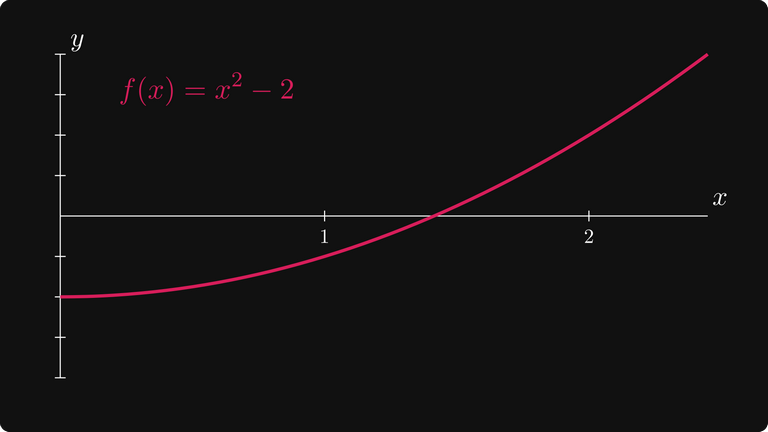
График f(x) = x² — 2
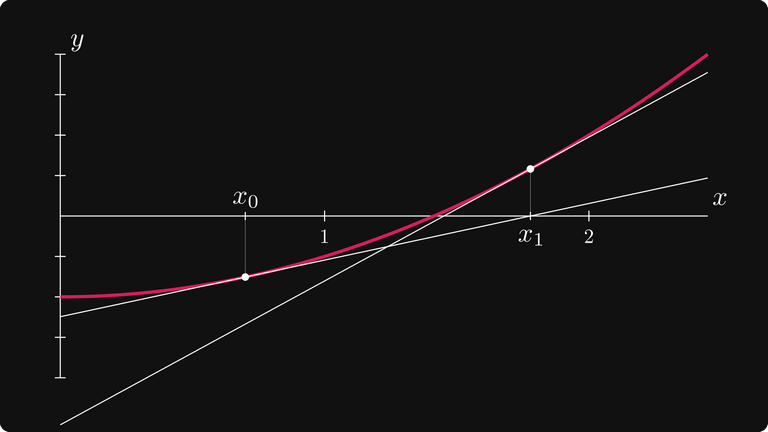
Как мы можем переместиться от нашей первоначальной догадки x₀ к корню?
Например, можно следовать по направлению касательной и посмотреть, где она пересекает ось X. Поскольку угол касательной определяет производная, это пересечение можно сразу вычислить. Я покажу, как это сделать.
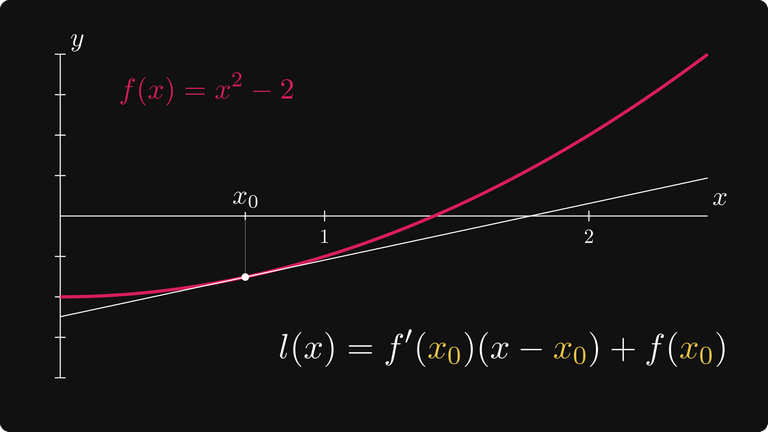
Уравнение касательной задаётся следующим образом.
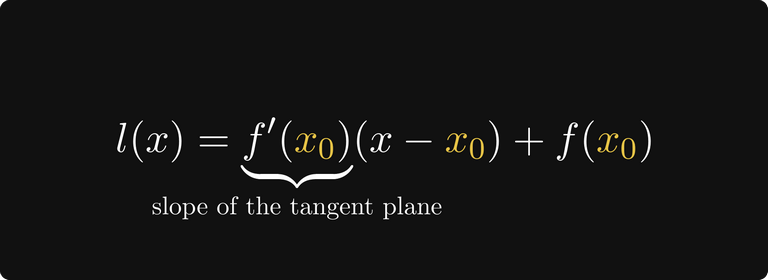
Приравняв его к нулю и решив, мы получим точку, в которой касательная пересекает ось X.
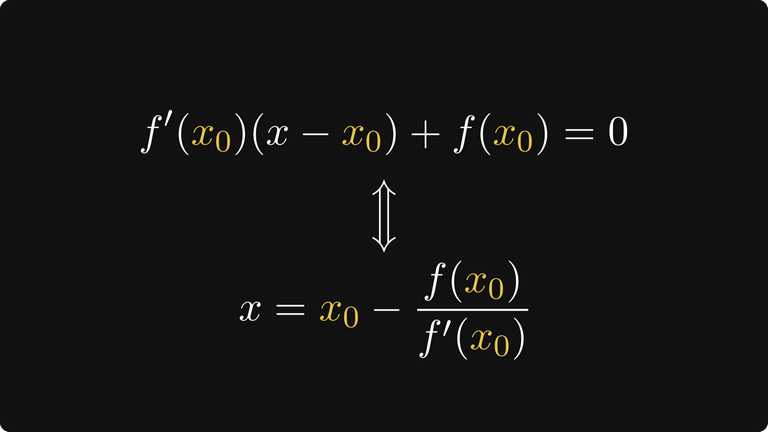
Таким образом, выбрав следующую догадку x₁ в качестве этой точки пересечения, мы получим более точную (надеемся) аппроксимацию.
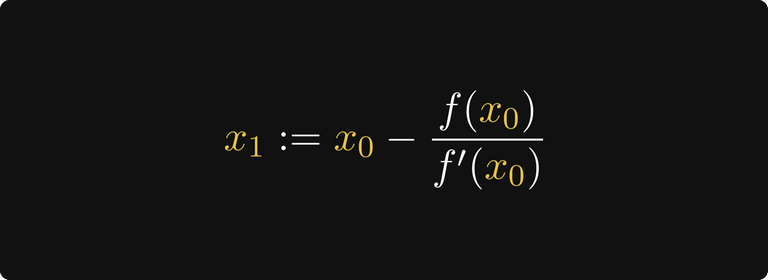
Вот и всё! На основании этой идеи мы можем определить рекурсивную последовательность.
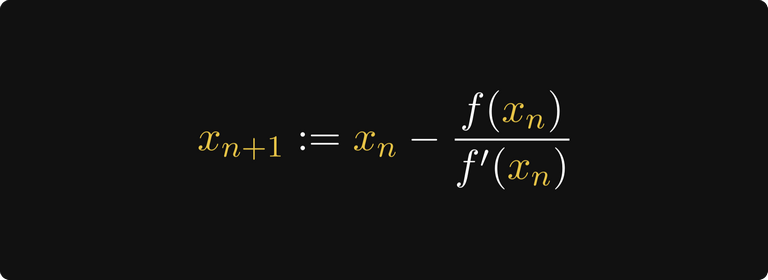
Это называется методом Ньютона-Рафсона. Вот следующий шаг. Как видите, третий шаг находится почти в √2.
Остаётся один важный вопрос: такой ли способ применили вавилоняне? Да, и вот почему.
Метод Ньютона-Рафсона и вавилонский алгоритм
В предыдущем примере мы решили найти корень f(x) = x² — 2. Давайте найдём явную формулу рекурсивной последовательности, заданной методом Ньютона-Рафсона. Её производную легко вычислить, так что мы готовы.
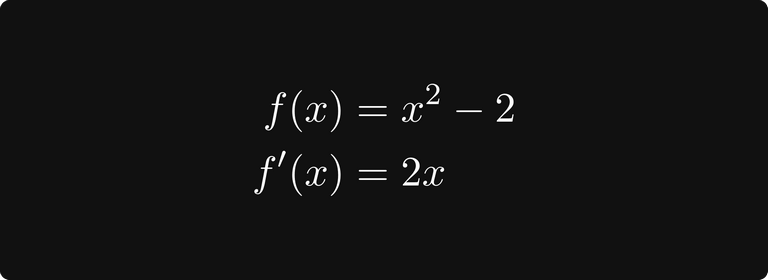
Применив немного алгебры, мы можем прийти к не особо удивительному выводу.
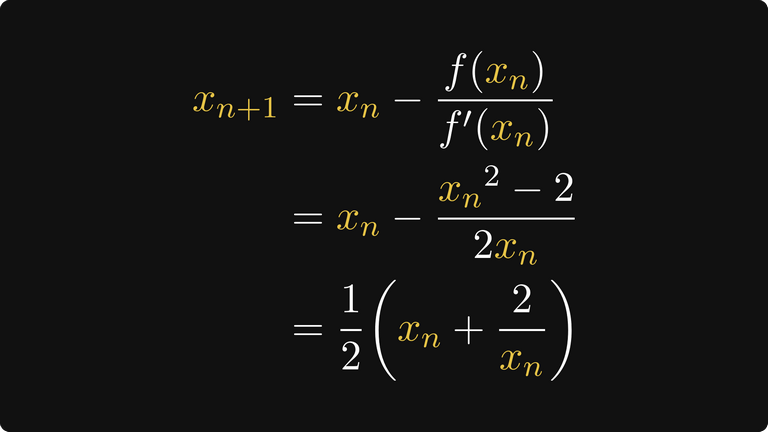
Следовательно, вавилонский алгоритм — это частный случай метода Ньютона-Рафсона!
Мы помним, что сходимость в этом конкретном случае крайне быстрая. Справедливо ли это в общем случае? Если нам повезёт.
Скорость сходимости
Если не вдаваться в подробности, сходимость и её скорость зависят от локального поведения функции.
Например, если f(x) дважды дифференцируема, то член погрешности для n-ного элемента может быть описан членами производных и квадратом (n-1)-ной погрешности.
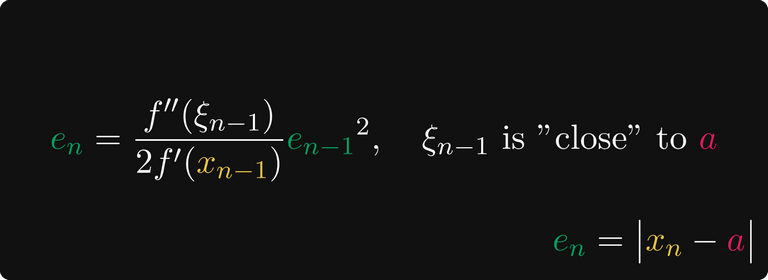
(Если вам интересны подробности, то доказательство есть в Википедии.)
В частности, если производные «ведут себя хорошо» (то есть первая производная отделена от нуля, а вторая производная ограничена), то скорость сходимости квадратичная.
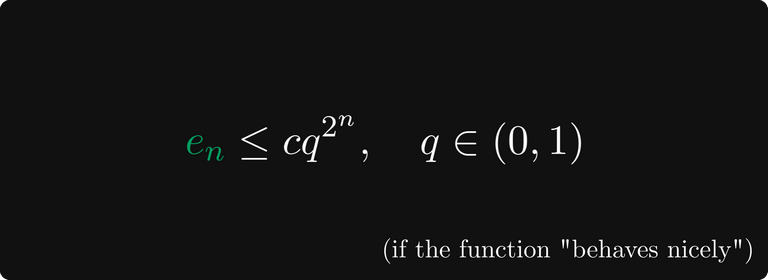
Если функция «ведёт себя хорошо»
Квадратичная сходимость истинна не только для поиска квадратного корня двух аппроксимацией положительного корня f(x) = x² — 2, но и для широкого спектра функций.
Недостатки
К сожалению не всё так идеально. Метод Ньютона-Рафсона может давать серьёзные сбои в довольно часто встречающихся случаях, к тому же имеет множество недостатков.
Например, если функция рядом с корнем «плоская», то сходимость будет мучительно медленной. Один из таких случаев показан ниже.
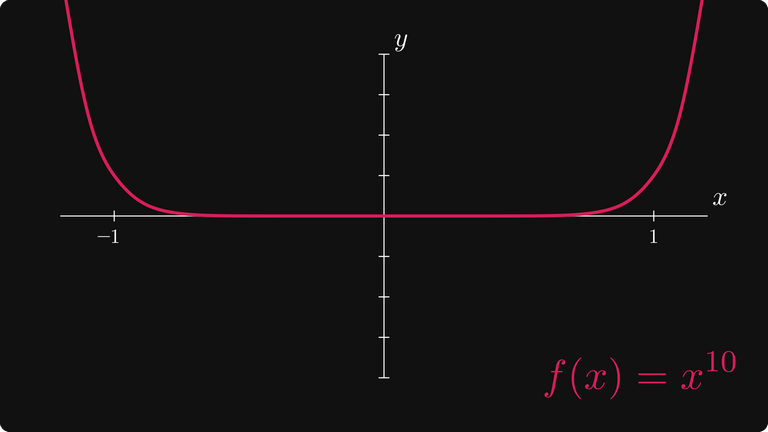
Это происходит, когда корень имеет большую повышенную неоднозначность, то есть производные тоже равны нулю. Кстати о производных, в отличие от случая с квадратным корнем вавилонян, их может быть сложно вычислить, из-за чего этот метод оказывается неприменимым.
Более того, весь процесс сильно зависит от первоначальной догадки: итерация может сойтись к неверному корню или даже разойтись.
Вывод
То, что древние вавилоняне смогли вычислить √2 до шестого знака после запятой, достаточно удивительно. Эта точность вызывает большое уважение, особенно учитывая, что она была достигнута почти четыре тысячи лет назад и вычисления выполнялись вручную.
Как оказалось, им не просто повезло; они обнаружили особый случай мощного метода, способного аппроксимировать корень широкого спектра функций. Он стал известен под названием «метод Ньютона-Рафсона».
Принцип прост:
- Предполагаем первоначальное значение x₀
- Временно заменяем функцию касательной к ней в x₀
- Определяем, где касательная пересекает ось X
- Используем это пересечение x₁ в качестве новой начальной точки процесса.
Если функция ведёт себя достаточно хорошо (то есть её производная локально отделена от нуля, а вторая производная ограничена), то сходимость происходит чрезвычайно быстро: именно поэтому вавилоняне смогли достичь «наивысшей в древнем мире вычислительной точности».
Автор:
digitalsibur






