Математика самонаводящихся ракет из аниме

Я создал прототип ракетной атаки! Для этого понадобилась хитрая математика, о которой будет рассказано в этой статье.

Мы поговорим о кубических кривых Безье, шуме Перлина и rotation minimizing frames.

Пусть Итиро Итано гордится.

В статье будет довольно мало кода, потому что основной упор мы сделаем на геометрию. Многих людей пугает математика, но помните, что необязательно понимать всё, чтобы ею пользоваться.

Итеративное и аналитическое движение

В общем случае существует два стиля написания кода движения. Итеративный код обновляет позицию объекта инкрементно кадр за кадром, выполняя процесс, который профессора колледжей называют интегрированием. Популярным примером такого стиля является метод Эйлера, при котором мы вычисляем вектор скорости объекта и на протяжении шага времени «подталкиваем» позицию в этом направлении:

void Update( float DeltaTime ) {
	Vector3 Velocity = CalculateVelocity();
	Vector3 Position = GetPosition();
	SetPosition( Position + DeltaTime * Velocity );
}

Дельта (Delta) — это просто математическое обозначение «изменения», например, «изменение со временем этого Update()»

Это естественный способ создания управления персонажем, при котором ввод игрока в каждом кадре меняется, или в сложных физических симуляциях, где нет известного аналитического решения для реального времени.

Если же вы знаете всё движение заранее, можно использовать аналитический код, в котором весь путь вычисляется по начальным условиям (математики называют это параметрической кривой), после чего сэмплируется текущее время. Хорошим примером этого является известная кубическая кривая Безье:

Vector3 CalcBezierPos( Vector3 P0, Vector3 P1, Vector3 P2, Vector3 P3, float t ) {
	float t_ = 1 - t;
	return
		(t_ * t_ * t_)    * P1 + 
		(3 * t_ * t_ * t) * P2 +
		(3 * t_ * t * t)  * P3 + 
		(t * t * t)       * P4 ;
}

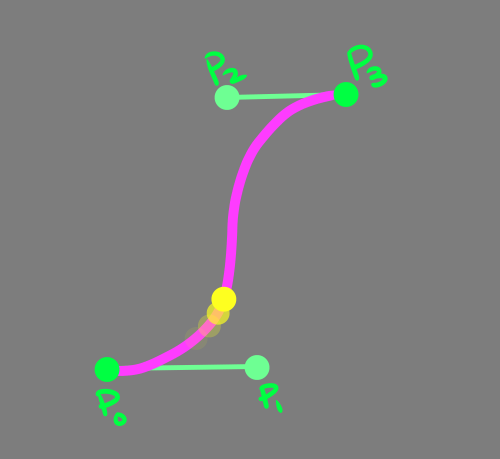
Если вы когда-нибудь работали с векторным редактором, то узнаете её. Кривые Безье — это кубические многочлены, то есть это простейшие контуры с четырьмя степенями свободы: конечными точками P0 и P3 и «контрольными точками» P1 и P2, влияющими на ориентацию и кривизну.

Входное значение t называется входным параметром, это коэффициент в интервале 0-1. То есть, например, t=0.333 — это примерно треть пути. Чтобы переместить точку, мы просто берём время, прошедшее с начала движения, и делим на общую длительность движения.

float StartTime;
float Duration;

void Update() {
	float CurrentTime = Time.time;
	float Elapsed = CurrentTime - StartTime;
	if( Elapsed >= Duration )
		SetPosition( P3 ); // мы в конце
	else
		SetPosition( CalcBezierPos( P0, P1, P2, P3, Elapsed / Duration ) );
}

Кроме позиции мы также можем использовать параметры кривой Безье для вычисления производной в t, то есть скорости изменения. Этот вектор полезен, потому что он касателен к кривой, то есть указывает в направлении движения. Чтобы преобразовать его в скорость, нужно разделить его на общую длительность.

Vector3 CalcBezierDeriv( Vector3 P0, Vector3 P1, Vector3 P2, Vector3 P3, float t ) {
	float t_ = 1 - t;
	return  (
		( 3 * t_ * t_ ) * ( P1 - P0 ) + 
		( 6 * t_ * t ) * ( P2 - P1 ) + 
		( 3 * t * t ) * ( P3 - P2 ) ;
}

float Velocity = CalcBezierDeriv( P0, P1, P2, P3, Elapsed / Duration ) / Duration;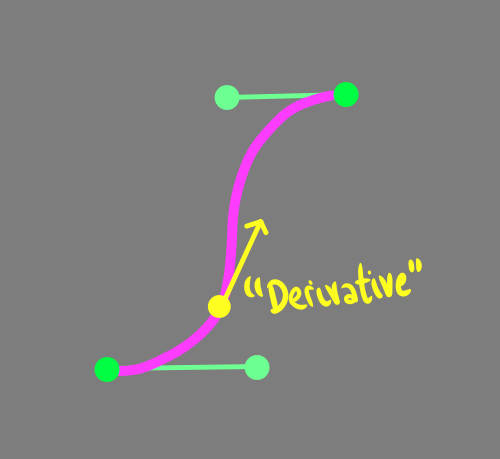

Speed = Meters Per Second = ( Meters Per T ) / ( Seconds Per T ) = Deriv / Duration

Симулируем самонаводящиеся ракеты

Так как я знаю, где начинается путь самонаводящейся ракеты (пусковая установка), и где он заканчивается (нарисованная цель), я решил использовать в качестве основы для пути ракеты кривую Безье.

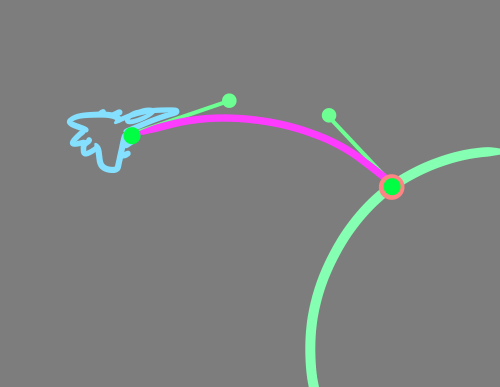
P1 помещена перед истребителем, а P2 проецируется из поверхности цели.
Использование аналитического решения упрощает работу, потому что нам не нужно вычислять сложную «симуляцию», попадающую в нужное место, и есть возможность точно настроить время между выстрелом и попаданием, что более интуитивно понятно, чем физические величины второго порядка.

Вполне приемлемый эффект, однако довольно скучный. Можно его улучшить.

Добавляем шум

Создав фундамент, можно приступить к украшательствам. Ракетные атаки в аниме движутся по хаотичным путям, увеличивая динамику. Мы можем имитировать это, добавив шум.

Художники по спецэффектам обычно используют шум Перлина — псевдослучайные колебания, они хаотичны, но плавны. Код шума слишком длинный, чтобы публиковать его здесь, но примеры легко найти онлайн.

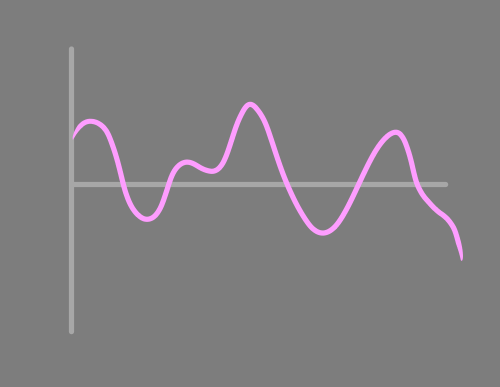
Поищите симплекс-шум (название популярного оптимизированного варианта).

Здесь возникает очевидная проблема: мне нужно, чтобы смещение в конечных точках было равно нулю, так ракета будет выровнена относительно пусковой установки и цели. Я решил её, выполнив умножение на огибающую, которая равна нулю на концах и единице посередине.

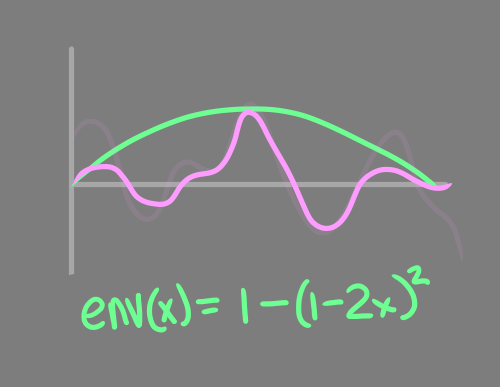
Как превратить функцию шума в смещение, искажённое по 3D-кривой? Мы вычислим два независимых значения шума и используем их в качестве компонент X и Y вектора смещения, преобразованного по кадрам поворота, привязанного к производной кривой Безье.

Vector3 LocalOffset;
float NoiseFreq = 2f; // коэффициент частоты вихляния
float NoiseAmp = 8;   // коэффициент величины вихляния
float Envelope = 1 - (1 - 2 * t) * (1 - 2 * t);
LocalOffset.x = NoiseAmp * Envelope * Noise( NoiseSeedX, NoiseFreq * Elapsed );
LocalOffset.y = NoiseAmp * Envelope * Noise( NoiseSeedY, NoiseFreq * Elapsed );
LocalOffset.z = 0;
Quaternion Frame = Quaternion.LookRotation( CalcBezierDeriv( P0, P1, P2, P3, t ) );
SetPosition( CalcBezierPos( P0, P1, P2, P3, t ) + Frame * LocalOffset );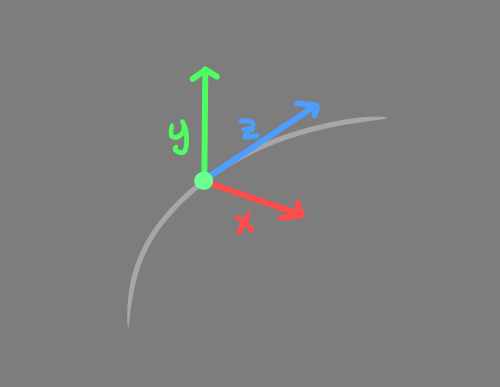

Ракета вихляет по красной и зелёной стрелкам

Это почти сработало, однако иногда возникали глитчи. Вычисленные таким образом закреплённые по вертикали кадры поворота привязаны к производной, но часто вращаются, особенно когда путь вертикальный. Вместо этого нам нужны так называемые Rotation Minimizing Frame, не имеющие мгновенного вращения и обладающие лишь минимальными покачиваниями между направлениями.

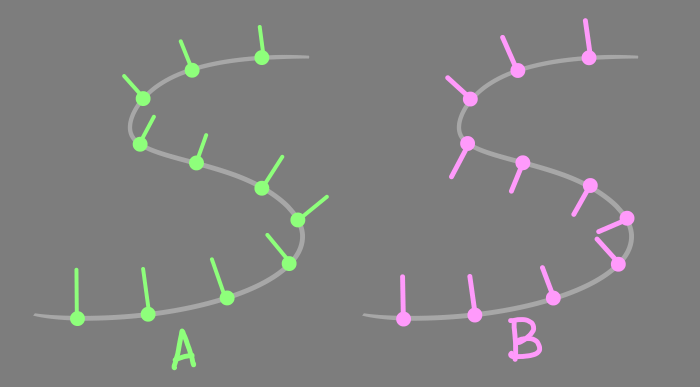
(A) Закреплённые по вертикали кадры (B) Rotation Minimizing Frames

Методика вычисления minimizing frames в общем случае математически сложна, но, к счастью, в 2006 году была опубликована статья, в которой приведён удивительно простой «подталкивания» кадра без вращения под названием Double Reflection Method. Нам необязательно разбираться с выводом, достаточно знать, что он малозатратен и работает.

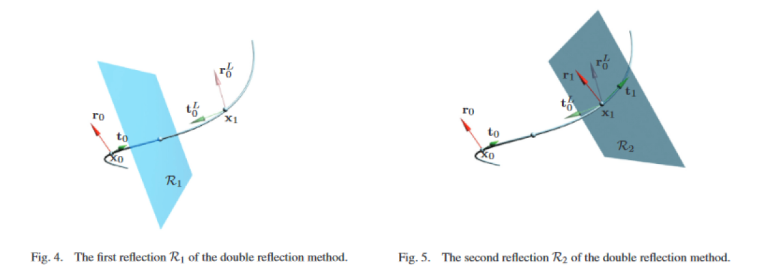
Quaternion Frame; // Инициализируем со значением Quaternion.LookDirection( P1 - P0 );

void UpdateFrame( float t ) {
	// "нормаль" и "касательная" начала
	var n0 = Frame * Vector3.up;
	var t0 = Frame * Vector3.forward;

	// "касательная" цели
	var t1 = CalcBezierDeriv( P0, P1, P2, P3, t ).normalized;

	// первое отражение
	var v1 = CalcBezierPos( P0, P1, P2, P3, t ) - GetPosition(); 
	var c1 = v1.sqrMagnitude;
	var n0_l = n0 - (2 / c1) * Vector3.Dot(v1, n0) * v1;
	var t0_l = t0 - (2 / c1) * Vector3.Dot(v1, t0) * v1;

	// второе отражение
	var v2 = t1 - t0_l;
	var c2 = v2.sqrMagnitude;
	var n1 = n0_l - (2 / c2) * Vector3.Dot(v2, n0_l) * v2;

	// создаём поворот, используя в качестве оси "вверх" нормаль цели
	Frame = Quaternion.LookRotation( t1, n1 );
}

Получилось!