Многие удобные нам вещи — результат чьих-то расчётов. Благодаря людям, которые заняты этими расчётами, большинство может спокойно забыть о том, что многие важные аспекты нашей жизни зависят от чисел и их свойств. К старту нашего флагманского курса по Data Science напоминаем о математической красоте формата бумаги A4.
Если вы не из США и не прогуливали большую часть учёбы и работы, вы наверняка имели дело с форматом A4. Вы не задавались вопросом, почему формат этот имеет именно такой размер? Давайте смахнём пыль со школьного учебника по математике и разберёмся во всём.
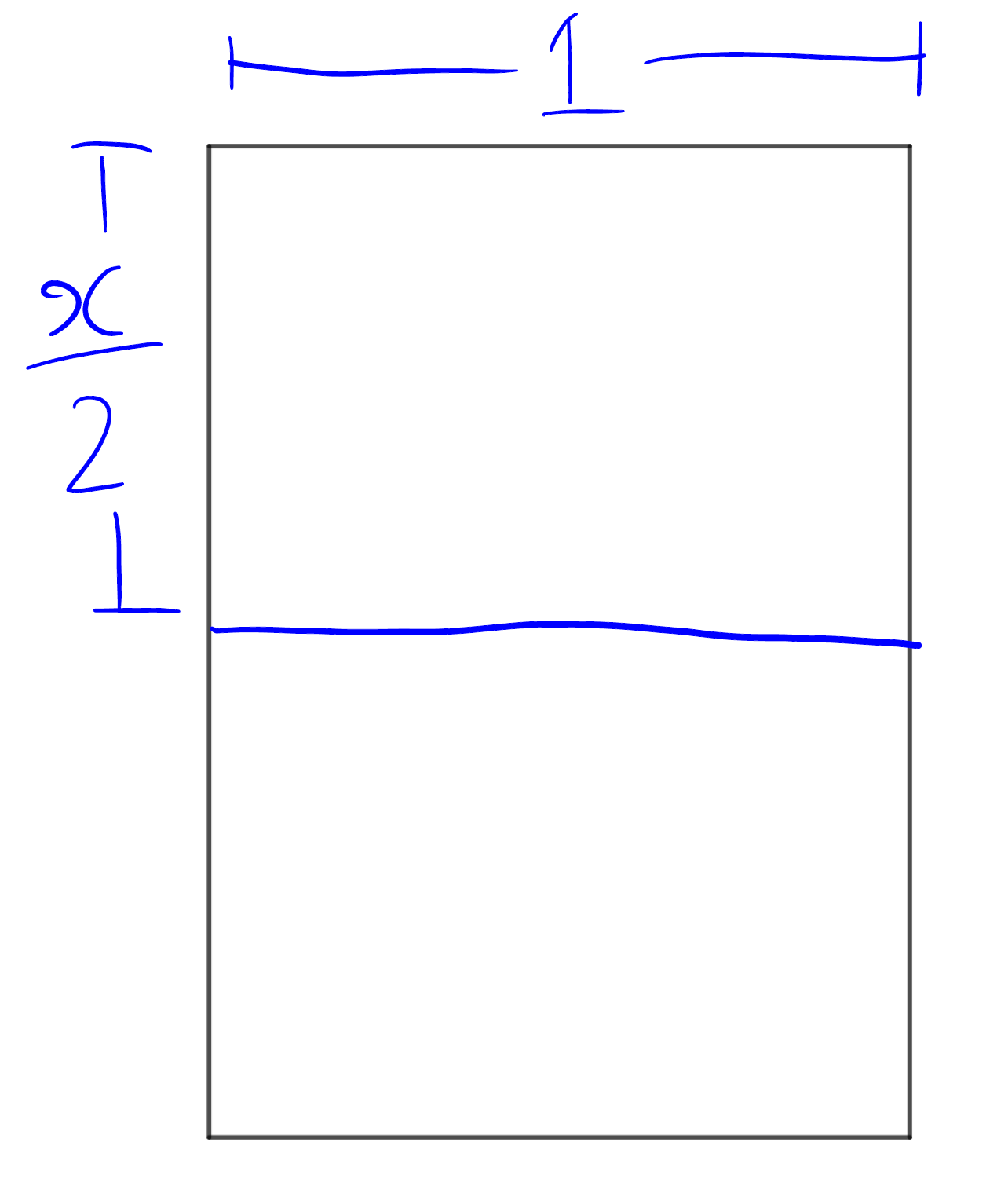
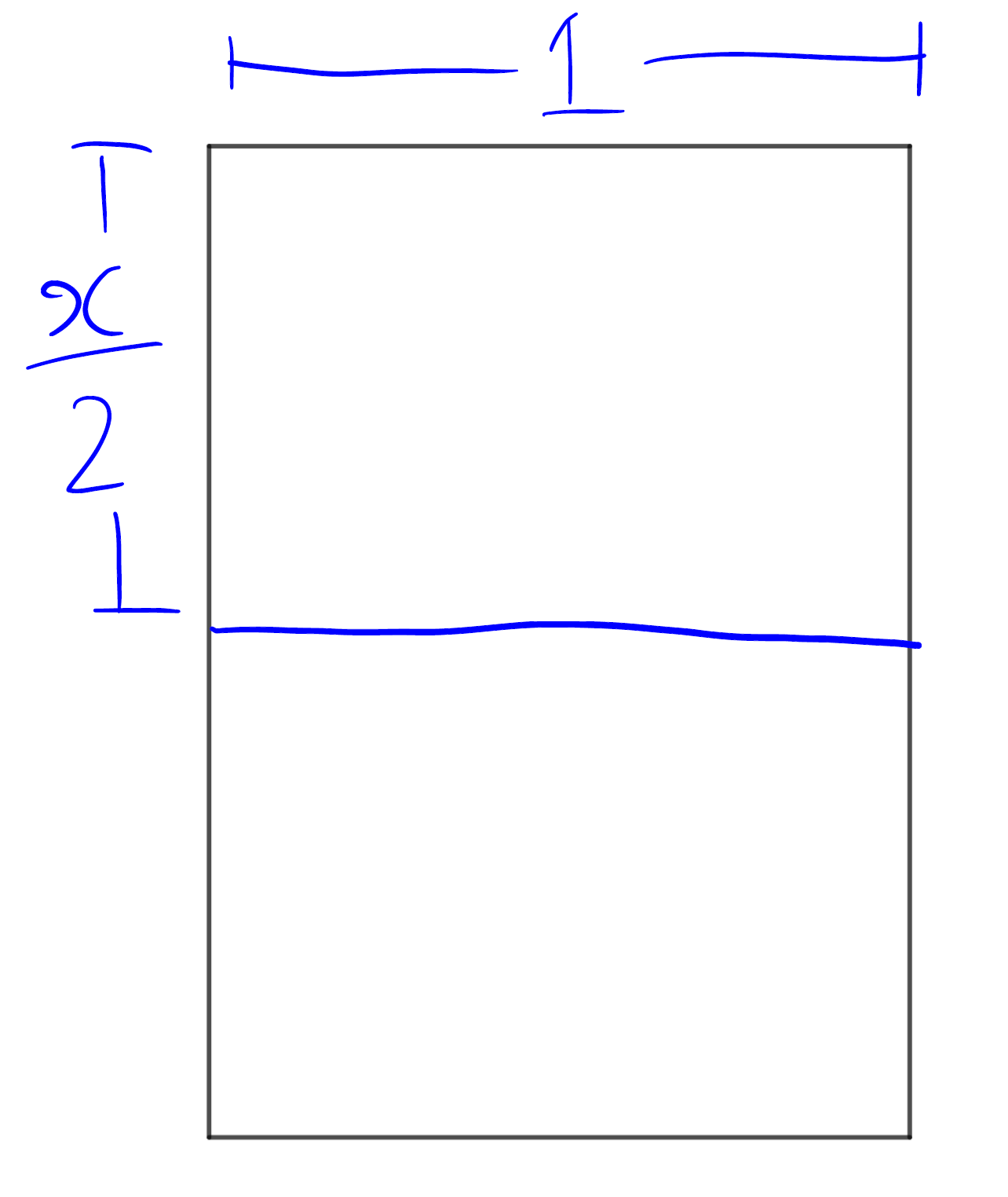
Сообщу вам формат бумаги на случай, если вы его всё-таки не знаете. Это ровно 210 на 297 мм. Можете не верить мне на слово. Проверьте. Я подожду. Если у вас в доме не завалялось ни одного листа А4, вы гораздо тщательнее делаете уборку в доме, чем я… Мерить такой лист удобно обычной 30-сантиметровой линейкой, которая наверняка найдётся в ящике вашего стола или неподалёку от него. Теперь остаётся только один вопрос:
Почему?
И вслед за этим зачастую мы спрашиваем: «Вы это серьёзно? 297 миллиметров? А почему не 300?» Я знаю, что это искреннее недоумение. Эти слова до сих пор звучат у меня в ушах с того школьного урока черчения, на котором один из моих товарищей именно в такой форме сетовал об извращённости нашего мира. Не помню, получил ли он ответ, но боюсь, что его боль по этому поводу так никто и не разделил. Давайте потратим остаток статьи на утешение страданий этого мальчика.
Воистину — каждый, кто когда-либо хотел отмерить половину листа бумаги, испытал лёгкое негодование. Немудрено: отмерить нужно 148,5 мм, а на линейке нет полумиллиметровых делений.
Предлагаю вам взять прямоугольный лист бумаги, отличный от листа формата А4. Ведь никто не мешает вам оторвать немного бумаги формата А4, а затем аккуратно сложить ее в прямоугольник. Взяв прямоугольник, отличный от А4, попробуйте сложить его ровно пополам [сверху вниз]. Вы увидите, что теперь лист бумаги вдвое меньше по размерам и совсем другой формы. Возможно, вы начали с «почти квадратного» прямоугольника, а теперь он стал «длинным и тонким», или наоборот.
Теперь проделайте это с листом A4. Кажется, вы уже поняли, что произойдёт. Вы получите формат A5. Он составляет половину формата А4 (ещё бы: вы же пополам складывали). Более того, форма осталась той же. Строго говоря, форма осталась аналогичной, соотношение сторон сохранено. Если вы хоть немного задумаетесь об этом, вы будете поражены. Ведь обычно прямоугольники так себя не ведут.
Возможно, эта «случайность» была одной из лучших идей XVIII века. Но пример приведу из наших дней: учителя уже много лет пользуются этим, чтобы буквально ополовинить свои затраты на ксерокопирование материалов. Хотите две копии на листе? Запросто — они отлично там уместятся! Но стоит взять любой другой формат (хотя бы, 8,5 х 11 дюймов, который североамериканцы величают «letter size») — и вы увидите, как куча бумаги уйдёт на совершенно ненужный зазор между двумя страницами.
Первая известная дискуссия по этой теме датируется 1786 годом — как и письмо от немецкого академика Георга Кристофа Лихтенберга его не менее известному соотечественнику Иоганну Бекману[1].
Однако есть предположения, что соответствующая задача давалась на экзаменах студентам задолго до этого[2].
Тем не менее только в ХХ веке Германия — а вслед за ней и большая часть мира — отразила эту идею в стандарте. Международный стандарт для формата бумаги получил номер ISO 216[3]
На самом деле существует лишь одно соотношение сторон прямоугольника, которое даёт аналогичную форму при складывании вдвое. Как вы думаете, какое? Нет, это не «золотое сечение», но тоже весьма интересное соотношение. Дальше я напишу, как его рассчитали.
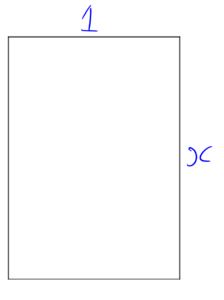
Построим обычный прямоугольник с соотношением сторон (длинная к короткой) 
:
Теперь проведём линию половинного сгиба, чтобы получить прямоугольник с соотношением сторон (длинная к короткой) 
.
Если мы, во имя всех упомянутых благ, хотим, чтобы два соотношения были одинаковыми, мы должны получить равные дроби
(или 
, об отрицательных соотношениях поговорим в другой раз).
Этим важным свойством обладает только одно соотношение. Это квадратный корень из 2, который, как известно (а в данном случае — по иронии судьбы), дробью не является. Поэтому размеры бумаги, в каких бы величинах вы их ни измеряли, не будут целочисленными и, с точки зрения многих людей, «красивыми». Поскольку ни одна пара чисел не даст отношения 
, приходится прибегать к приближённым значениям.
Поэтому мы должны (и смогли) отказаться от мечты о «красивой» длине сторон, что не мешает нам получать «красивые» площади. На самом деле, современная международная система форматов «А» начинается с бумаги формата А0, со сторонами в правильном соотношении 
, но с площадью ровно 1 м2, или настолько близкой к ней, насколько это возможно при длине сторон в целых миллиметрах (1189 х 841 мм, если быть точным). Теперь складывайте этот лист вдвое и режьте его, пока он не уместится в папку и не станет удобным для работы. Вы получите формат A4, отсюда и «4» в названии.
Кстати, если вам всё это в новинку, но помнится кое-что из школьного курса математики, вам может понравиться другой способ понять это. Помните «коэффициенты масштаба площади» и «коэффициенты масштаба длины»? Коэффициент масштаба площади тождественно равен квадрату коэффициента масштаба длины. Так вот, если вы хотите, чтобы коэффициент масштаба площади был 
(или 
), коэффициент масштаба длины должен быть 
(или 
). Конечно же, вы помните.
Нравится вам это или нет, но иррациональные числа полезны. Звучит отрезвляюще. А для некоторых — удручающе. Вспомним хотя бы миф о том, что сделали пифагорейцы с Гиппасом, который назвал выражение 
иррациональным). Но, как только мы преодолеем страх перед иррациональными величинами, мы сможем пожинать плоды. Теперь вес бумаги легко рассчитать, потому что он пропорционален площади: бумага плотностью 80 грамм на (квадратный) метр формата А0 весит ровно 80 г. Бумага формата А4 такой плотности весит 5 г, так как её сложили пополам 4 раза [уменьшили в 24, то есть в 16 раз].
Ширина стержня линера увеличивается на коэффициент $inline$sqrt{2}~1.4$inline$. Таким образом, следующий линер в наборе подойдёт для следующего формата бумаги. Вот так красиво всё устроено.
Чертёжные ручки с маркировкой размера (с увеличением на коэффициент 1,4). Wikimedia Commons
Какой из этого можно сделать вывод? Многие удобные нам вещи — результат чьих-то расчётов. Благодаря им мы теперь можем спокойно забыть, что многие важные аспекты нашей жизни зависят от чисел и их свойств. Благодаря тому, что кто-то об этом не забыл.
Да, обо всем этом мы можем спокойно забыть. Но прошу вас: вспомните об этом, когда кто-то снова решит отмерить пол-листа, и вы снова услышите глас вопиющего в пустыне: "Ну почему 297?" Теперь вы знаете, что ответить.
[1] Тот самый Лихтенберг, который дал своё имя фигурам Лихтенберга, рисункам искровых разрядов высокого напряжения. И тот самый Бекман, который ввёл в науку термин «технология». Теперь вы это знаете.
[2] https://www.cl.cam.ac.uk/~mgk25/lichtenberg-letter.html.
Стать востребованным профессионалом в IT с самого начала или прокачаться помогут наши курсы. Скидка 45% по промокоду HABR:
Автор:
honyaki
