
Начнём мы конечно же с теории и дадим определение кольцевому маршруту и его возможным частным случаям. Кольцевой маршрут — маршрут движения автомобиля по замкнутому контуру, соединяющему несколько потребителей (поставщиков). Разновидностями кольцевых маршрутов являются развозочные, сборные и сборно-развозочные маршруты. Развозочным называется такой маршрут, при котором продукция загружается у одного поставщика и развозится нескольким потребителям. Сборочный маршрут — это маршрут движения, когда продукция получается у нескольких поставщиков и доставляется одному потребителю. Сборно-развозочный маршрут — это сочетание развозочного и сборочного маршрутов.
Построение графа
Поскольку развозочные и сборочные маршруты частные случаи кольцевых маршрутов, а мы стремимся создать универсальный автоматизированный расчёт показателей, то все усилия сосредоточим на классическом кольцевом маршруте.
По большей части конструкция графа повторяет тот же принцип, что был описан уже в в посте с маятниковыми маршрутами (тут). Для начала создаём набор грузопунктов и соединяем их линиями:
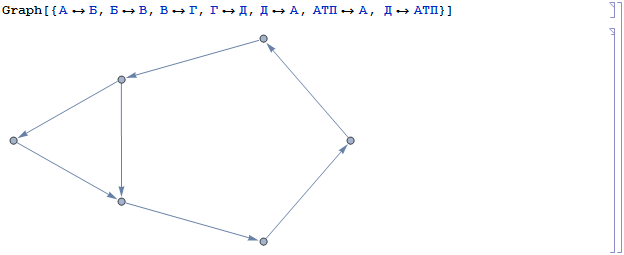
Затем добавляем для каждой линии и грузопункту текстовые метки, а так же разделяем груженные ездки от холостых и нулевых:

Добавляем другие свойства, улучшая внешний вид графа в целом:
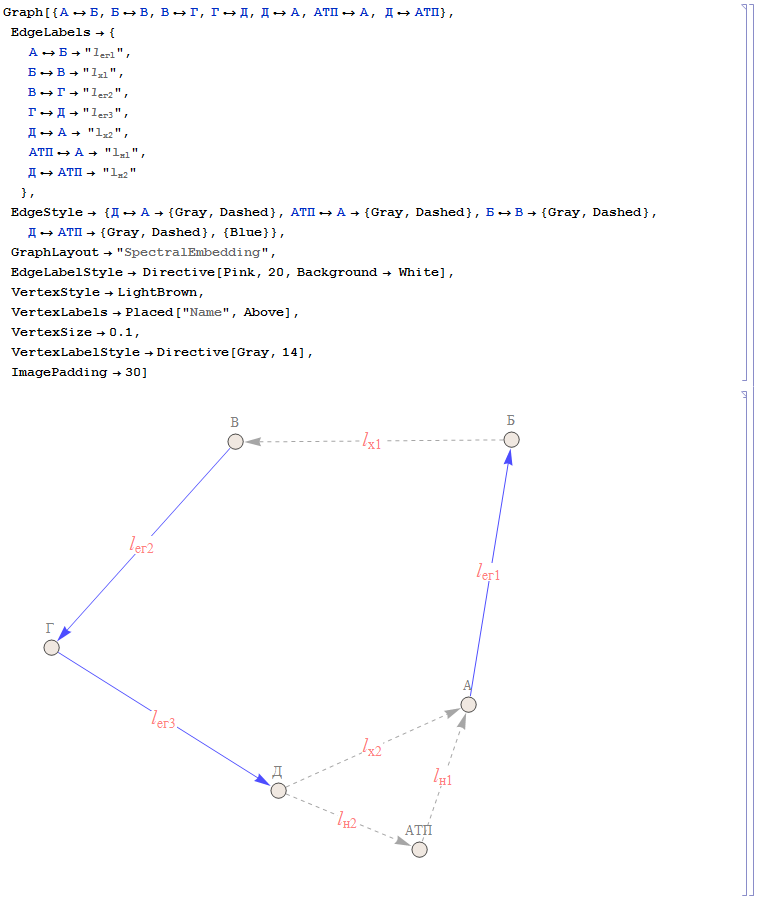
Каждой свойство мы либо уже обсуждали, либо их название говорит само за себя. Единственное что вызывает недоумение, почему я выбрал SpectralEmbedding, а не CircularEmbedding, которое так и напрашивается в нашем случае. Дела в том, что CircularEmbedding делает граф слишком угловатым, простым и некрасивым. Вот и все.
Дано

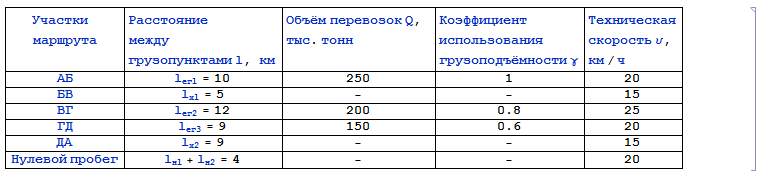
Решение
1. Определяем время работы автомобиля на маршруте, ч:

2. Устанавливаем время оборота автомобиля, ч:

3. Определяем число оборотов автомобиля на маршруте за время работы:
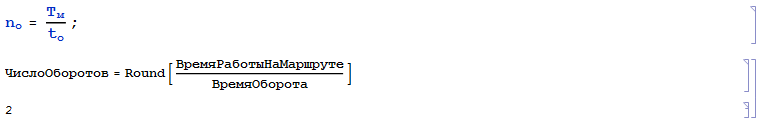
4. Пересчитываем время работы автомобиля на маршруте и в наряде в связи с округлением числа оборотов, ч:
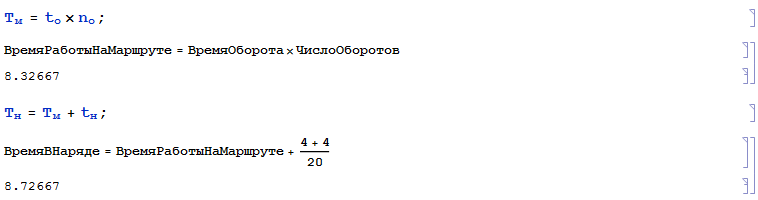
5. Определяем дневную выработку автомобиля в тоннах и тонно-километрах:

6. Определяем необходимое количество автомобилей для работы на маршруте:

7. Определяем суточный пробег автомобиля, км:
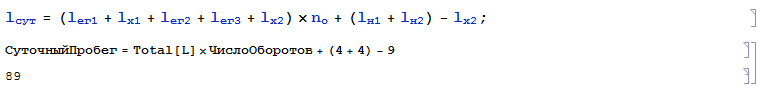
8. Коэффициент использования пробега на маршруте:

Автоматизация расчёта показателей кольцевых маршрутов
При расчёте показателей для маятниковых маршрутов мы уже выработали структуру и отказываться от неё было бы грешно. Поэтому я не стану вдаваться в подробности её строения, так как сделал это в посте с маятниковыми маршрутами (и снова отсылка сюда).
Но кольцевые маршруты имеют одну отличительную особенность — количество грузопунктов в маршруте не ограничено, а значит мы должны дать возможность пользователю вводить столько данных, сколько он посчитает нужным. Для этого сначала модифицируем InputField так, чтобы поле могло принимать не ограниченное количество значений. Звучит сурово, но на самом деле достаточно поменять свойство этого поля на String, то есть чтобы оно принимало строки, а не отдельные числа:

Это порождает проблему, так как мы не может подставлять строки в формулу не переведя их предварительно в числовое значение. Для этого создаём модуль convert:

Принцип работы модуля:

Как видите, модуль convert достаточно устойчив к возможному нестандартному вводу, ошибкам в виде пропущенной запятой или точки вместо запятой.


Используемая литература
Неруш Ю. М. Логистика: учеб. — 4-е изд., перераб. и доп. — М.: ТК Велби, H54 Изд-во Проспект, 2008 — 520 с.
ISBN 978-5-482-01995-5
Рекомендую купить, например, здесь: OZON.ru
Исходники
Проект в виде репы на GitHub — Wolfram-Math-in-Logistics
Буду очень рад видеть ваши вопросы, рекомендации и возможно форки.
Подборка ссылок
- Wolfram-Math-in-Logistics: Прогнозирование материалопотока и товарооборота;
- Wolfram-Math-in-Logistics: Маятниковые маршруты;
- Wolfram-Math-in-Logistics: Кольцевые маршруты;
- Ждите ещё.
Автор: iwi

