Змей и дротик. Путь от михраба до квазикристаллов

В 2020 году половину Нобелевской премии по физике получил Роджер Пенроуз. Премия была выдана с формулировкой «За открытие того, что образование чёрных дыр с необходимостью следует из общей теории относительности». Это произошло более чем через два года после смерти Стивена Хокинга, который наверняка бы получил эту премию, если бы дожил. Но она досталась Пенроузу (род. 8.08.1931) – человеку на 11 лет старше Хокинга, его коллеге и другу, вскоре перешагнувшему девяностолетний рубеж. После 2015 года я не могу избавиться от мысли, что Нобелевская премия (особенно по литературе) изживает себя, как и олимпийские игры, но как раз Роджер Пенроуз является одним из тех гранинских «зубров», который много ранее заслужил несуществующую Нобелевскую премию по математике. Я был причастен к переводу его книги «Мода, вера, фантазия» на русский язык, и именно в тот период познакомился с сумрачным гением и скверным характером этого человека, а также с дивными мирами, рождающимися у него в голове. Пенроуз как никто из наших современников выразил платоновские идеи о высшем мире идеальных фигур, воплощения которых когда-нибудь найдутся и в реальном мире. Именно об этой грани его исследований пойдет речь под катом: о геометрических паркетах, мозаике Пенроуза и квазикристаллах Шехтмана.

Центральную роль в типичных геометрических узорах играет симметрия. Большинству живых существ присуща зеркальная симметрия, а некоторым, например, морским звездам и радиоляриям – лучевая. Вероятно, именно поэтому симметрия кажется нам гармоничной и красивой. 

В геометрических узорах понятие симметрии тесно связано с понятиями периодичности и замощения. Простейший пример и того, и другого – разделение плоскости на клетки. Такой узор абсолютно симметричен: за каждым квадратом начнется следующий квадрат. Более сложным вариантом такого узора являются геометрические паркеты, известные как на плоскости, так и на сфере. Паркет можно замостить не только геометрическими фигурами, но и изображениями, в чем особенно преуспел знаменитый голландский художник Мауриц Эшер (1898-1972). Из паркетных мозаик Эшера мне наиболее нравятся «Ангелы и демоны».

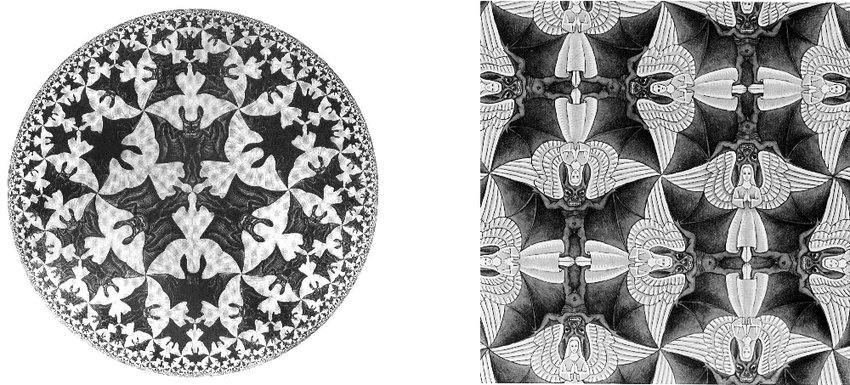
Такие паркеты, древнейшие из которых были известны еще Евклиду, эстетически привлекательны, но с геометрической точки зрения незамысловаты. Это просто периодический узор, которым можно замостить любую плоскость, и который в любой ее точке будет выглядеть одинаково. Гораздо интереснее апериодические мозаики – то есть, замощения, сохраняющие симметрию, но при этом нигде не повторяющиеся. В свою очередь, любой фрагмент апериодической мозаики уникален, и его не удастся наложить на идентичный фрагмент методом параллельного переноса, поскольку идентичного фрагмента не существует.

Исламские геометрические узоры

В Средневековье геометрические мотивы активно исследовались в арабском изобразительном искусстве. Это было связано не только с тем, что ислам запрещает изображать человека, а тем более – Аллаха, но и с тем, что Халифат обладал широким доступом к античным научным трактатам, переводившимся на арабский язык. Сложно сказать, пришли ли арабские геометры и архитекторы к понятию (а)периодичности, однако, они широко применяли и усложняли мозаичную технику гирих, представляющую собой звездчатые симметричные орнаменты:

Эта техника, возникшая в Сирии около III века н.э., могла более или менее спонтанно привести к созданию апериодической мозаики. Наиболее известным образцом (псевдо)апериодического гириха является фасад мечети имама Аль-Дарби в иранской провинции Исфахан (XV век):

Прежде чем перейти к формализации этих узоров, обратим внимание: в этом гирихе доминируют пятиугольники. Именно пятиугольник – предпоследний шаг к апериодической мозаике Пенроуза, но начнем мы с более ранних примеров.

Путь к апериодической мозаике

В XV веке периодические замощения-паркеты были изучены в Европе уже достаточно хорошо, и были известны, в частности, следующие их свойства:

• Любым треугольником или четырехугольником можно замостить плоскость.

• Известно 15 типов пятиугольников, позволяющих замостить плоскость; неизвестно, является ли этот перечень полным.

• Известно 3 типа шестиугольников, позволяющих замостить плоскость

• Невозможно замостить плоскость одинаковыми выпуклыми многоугольниками с числом сторон, большим или равным семи.

В 1619 году Иоганн Кеплер написал трактат «Harmonices Mundi» («О гармониях мира»), где рассуждал о сочетаниях геометрических фигур. Именно в этой работе он интуитивно догадался, что можно попробовать замостить плоскость многоугольниками, так, чтобы узор нигде не повторялся. Для этого Кеплер попытался использовать пятиугольники (в том числе звездчатые), весьма напоминающие мусульманские узоры:

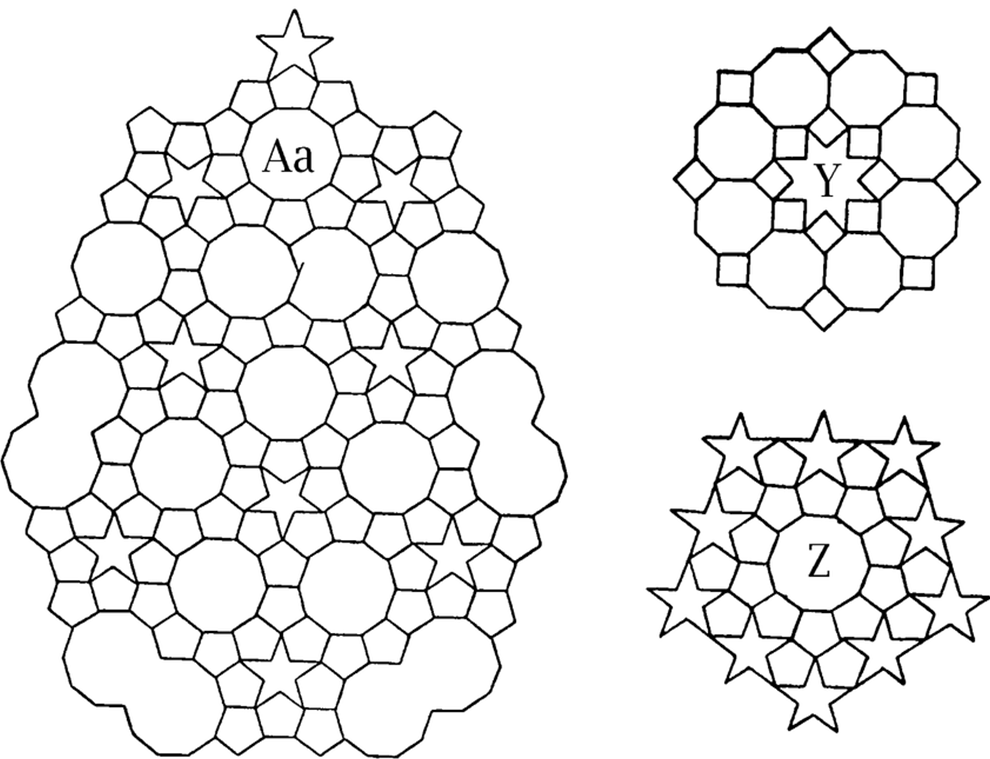
Правда, некоторая периодичность в мозаике Кеплера все-таки существует (то есть, в ней можно найти повторяющиеся участки). Длительные попытки построить полностью апериодический узор из конечного числа фигур на плоскости успехом не увенчались, и в 1961 году китайский математик Хао Ван предположил, что апериодических замощений не существует. Тем не менее, уже в 1966 году его ученик Роберт Бергер смог доказать, что существует множество из 20 426 разных фигур, которое действительно покрывает неограниченно обширную плоскость апериодической мозаикой. Вскоре сам Бергер смог сократить это множество до 104 фигур, а в 1971 году к задаче подступился Рафаэль Робинсон, показавший, что апериодическую мозаику можно сложить всего из 8 плиток, близких по форме к квадрату. Вот мозаика Робинсона:

В мозаике Робинсона плитки должны располагаться так, чтобы красные линии одной плитки стыковались с красными линиями другой плитки, а синие – с синими. Поскольку на некоторых плитках есть линии только одного цвета, очевидно, что это накладывает на компоновку мозаики Робинсона серьезные ограничения.

Наконец, в 1974 году Роджер Пенроуз предложил апериодическую мозаику, состоящую всего из двух многоугольников, которые он назвал «kite» (воздушный змей) и «dart» (дротик). Действительно, по форме они похожи на эти фигуры, но сами раскладываются на еще более мелкие треугольники:

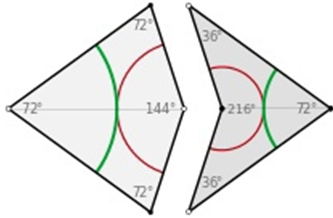
Из этих фигур далее складываются ромбы и параллелограммы, образующие структуру из пятиконечных звезд в обрамлении параллелограммов, причем соседние звезды повернуты относительно друг друга на 36 градусов:

До сих пор неизвестно, существует ли такая геометрическая фигура, чтобы только ее экземплярами можно было бы замостить плоскость – и получить апериодическую мозаику. Но змей и дротик Пенроуза увековечили его имя более чем за сорок лет до того, как Пенроуз получил Нобелевскую премию, и эта находка казалась не только сочетанием красоты, простоты и точности, но и чисто абстрактным геометрическим конструктом (как я упомянул во введении к этой статье, говоря о платонизме мозаики Пенроуза). Иными словами, даже Пенроуз изначально считал свою мозаику сугубо умозрительным узором.  Но уже в 1982 году его мозаика была обнаружена в природе.

Квазикристаллы

В 1784 году выдающийся минералог Рене Гаюи (1743 — 1822) на основе эмпирических наблюдений показал, что любой кристалл можно разбить на элементарные ячейки (шестигранные призмы) и получить образец кристаллической решетки фактически любого размера путем параллельного переноса этих ячеек. Таким образом, кристаллическая решетка стала пониматься как идеально симметричная структура (Гаюи не знал о существовании атомов, открытых Джоном Дальтоном только в 1803 году, поэтому полагал, что кристалл состоит из мельчайших шестиугольных частиц). Только в 1912 году, когда Макс фон Лауэ открыл дифракцию рентгеновских лучей на кристаллической решетке, появилось более точное определение кристалла: «то, что дает закономерную дифракционную картину при облучении рентгеном». С тех пор точную форму кристаллической решетки различных минералов или синтетических веществ было принято определять именно рентгенографическим методом. А в 1982 году американский ученый Алан Маккей подошел к такой процедуре с ровно противоположной стороны: попробовал смоделировать трехмерную мозаику Пенроуза в наномасштабе, так, чтобы сторона плитки была сопоставима с длиной рентгеновской волны. Получилась структура, напоминающая кристаллическую решетку, обладающая симметрией 10-го порядка.

Тем временем Дан Шехтман (род. 1941) из Тель-Авивского университета провел 1982-1983 годы в творческом отпуске (т.н. sabbatical) в университете Джонса Хопкинса в США, где и заинтересовался сплавами алюминия с переходными металлами, которые получают методом быстрой закалки. Этот метод, известный еще с конца XIX века, изначально использовался для уменьшения зернистости сплава и повышения его прочности, но, если сплав нагревался при работе, то быстро терял полезные свойства и становился хрупким. Опыты в этой сфере не прекращались, и в 1960 году в Калтехе методом сверхбыстрого охлаждения удалось получить первый в своем классе аморфно-металлический сплав золота и кремния Au₇₅Si₂₅. В 1976 году в Пенсильванском университете было получено значительно более удобное и дешевое вещество такого рода с решеткой NiFePB (никель-железо-фосфор-бор), где первые два элемента придают сплаву прочность, характерную для металлов, а вторые два обеспечивают аморфность и пластичность. Предполагалось даже, что такие вещества могут прийти на смену железобетонным конструкциям, но к моменту творческого отпуска Шехтмана имелась лишь отлаженная технология получения таких сплавов, не давшая серьезного практического результата. В апреле 1982 года Шехтман, рассматривая под микроскопом дифракционный узор алюминиево-марганцевого сплава Al₈₆Mn₁₄, увидел примерно следующее:

Пытаясь объяснить эту картину, Шехтман пришел к выводу, что наблюдает апериодическую симметрию наподобие икосаэдра, а описать расположение атомов в этом сплаве можно в виде трехмерного аналога мозаики Пенроуза:

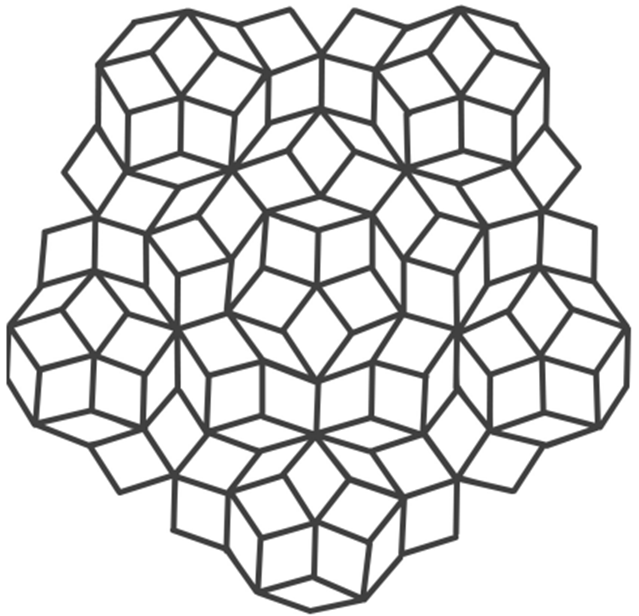
В 1984 году Дан Шехтман и Илан Блех подготовили статью о такой странной решетке, которая только в ноябре того же года была опубликована в «Physical Review Letters». Полученная структура получила название «квазикристалл», поскольку обладала симметрией, но не обладала периодичностью – таким образом, она является материальным воплощением мозаики Пенроуза. В ходе подготовки этой статьи Шехтман заявил, что не знал о моделировании Маккея; также оказалось, что сплав AlCuFe (алюминий-медь-железо) привлек внимание химиков своей странной дифракцией еще в 1939 году, но тогда еще не хватило теорбазы, чтобы распознать в нем икосаэдрический квазикристалл.

В 1987 году впервые удалось получить стабильный макроскопический квазикристалл и убедиться, что Шехтман описал новую форму организации материи, а не экзотический дифракционный эффект. В 1992 году Международный союз кристаллографии официально переопределил, что такое «кристалл» - новая формулировка звучит как «any solid, having an essentially discrete diffraction diagram», то есть «любое твердое вещество, обладающее отчетливо дискретной дифракционной картиной». В 2011 году Дэн Шехтман был удостоен Нобелевской премии по физике за это открытие.

Впоследствии, когда было открыто уже более 20 вариантов упорядочивания квазикристаллов, выяснилось, что они представляют собой не классический, а деформированный вариант мозаики Пенроуза, и атомы в них образуют хорошо различимые кластеры. Более точный рисунок квазикристаллической решетки (отсюда) выглядит вот так:   

Насколько мне удалось уточнить, в настоящее время еще не найдено отчетливо полезных вариантов применения квазикристаллов. Благодаря непериодичности, к этим веществам почти ничего не прилипает (пенроузовская антипригарная сковородка), а также они почти не изнашиваются, то есть, весьма перспективны в качестве покрытия для режущих кромок. Еще предстоит разобраться, как квазикристаллы пропускают свет и тепло, могут ли они принести реальную пользу в фотолюминесценции или, например, в качестве моделей для 3D-печати. Возможно, это тема для отдельной статьи или дискуссии. Мне же до сих пор неуютно осознавать, что Пенроуз получил Нобелевку за теоретические разработки в исследовании черных дыр, а не за платоническое предвосхищение симметрии, зародившейся где-то в переднеазиатских михрабах. Впрочем, Нобелевская премия по математике не существует (в отличие от квазикристаллов), а Нобелевская премия по физике пришла и к Шехтману, и к Пенроузу, пусть и с разницей в девять лет.