Когда-то очень давно, когда я был еще студентом, сидя на одной скучной лекции я задумался над тем, с какой частотой может колебаться в одной плоскости свободно висящая веревка или цепочка заданной длины и какова будет при этом ее форма, если колебания будут небольшими. Я помню, что решил эту задачу, но сейчас, по прошествии многих лет, уже забыл подробности того, как я это сделал. Однако, мне стало интересно восстановить это решение максимально подробно и поделиться им со всеми, кому это было бы интересно. Что из этого получилось, читайте под катом.
Пусть у нас есть цепочка длины l и массой M, подвешенная за один конец, как показано на рисунке. Здесь мы будем предполагать, что цепочка однородна и силами трения можно пренебречь. Построим систему координат таким образом, чтобы начало координат совпадало с точкой подвеса, ось X направлена вниз, а ось Y, перпендикулярная оси X, будет отвечать за отклонение цепочки от вертикали. Фактически, необходимо определить функцию Y(x,t).
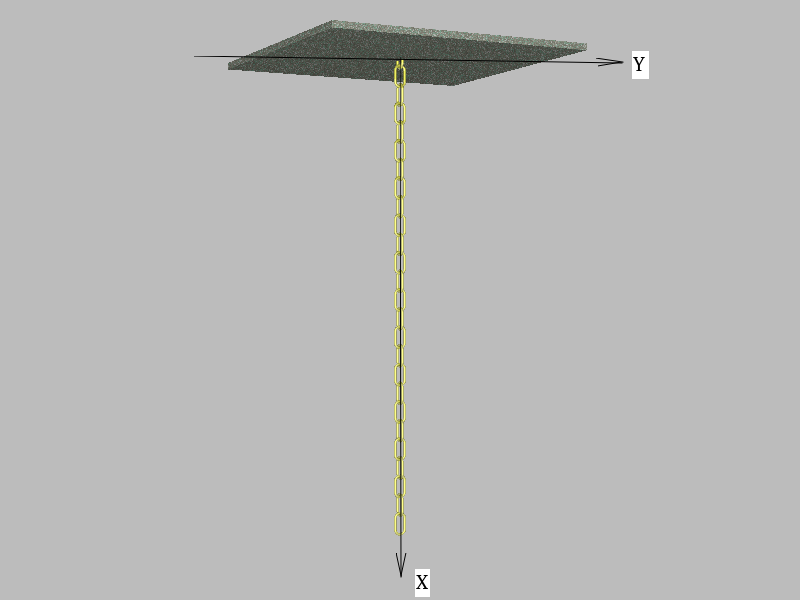
Чтобы найти Y(x,t) распишем силы, действующие на небольшой участок цепочки как показано на следующем рисунке.
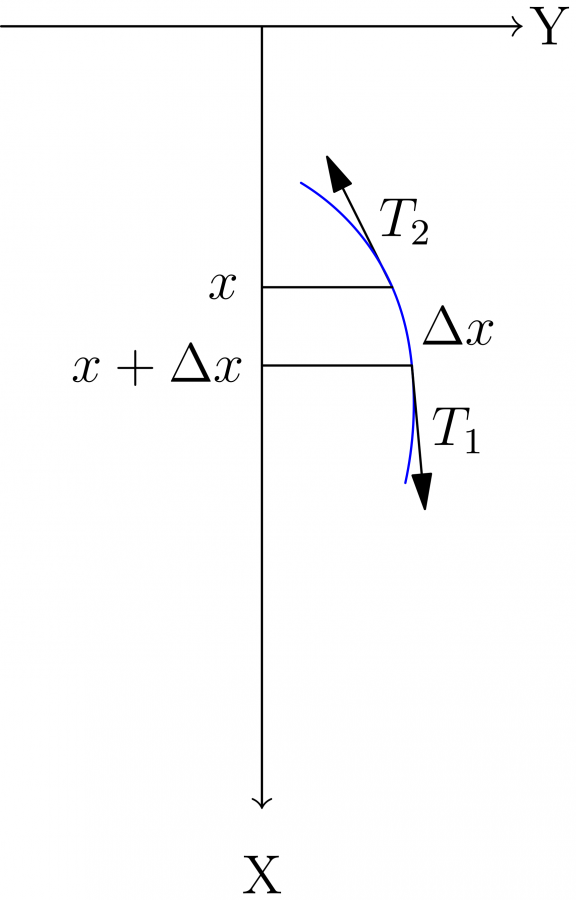
Из рисунка видно, что сила натяжения T является касательной к цепочке. Следовательно, тангенс угла наклона T к оси X будет равен производной dY(X)/dX. Известно, что если колебания небольшие, то тангенс примерно равен самому углу в радианах. Силу натяжения T можно рассчитать по формуле
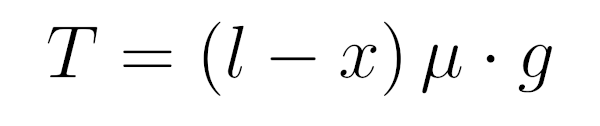
где l — длина цепочки, g — ускорение свободного падения, и
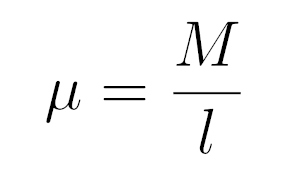
масса на единицу длины цепочки.
Запишем уравнение исходя из второго закона Ньютона
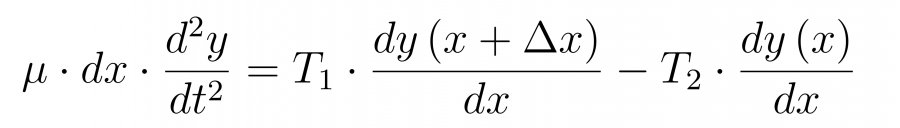
В правой части уравнения подставим значение натяжения T пока без соответствующего коэффициента
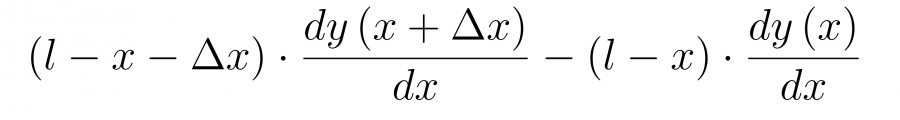
Заменим значение производной в точке x+dx через вторую производную
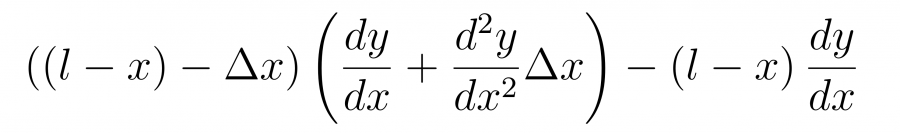
Раскроем скобки
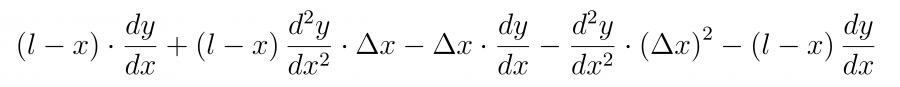
и сократим соответствующие слагаемые, убирая также слагаемое второго порядка малости.
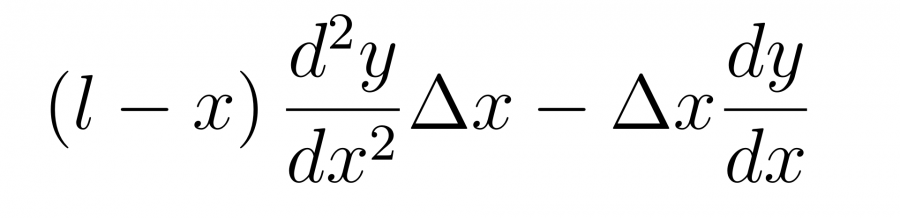
Подставим полученную формулу в уравнение движения
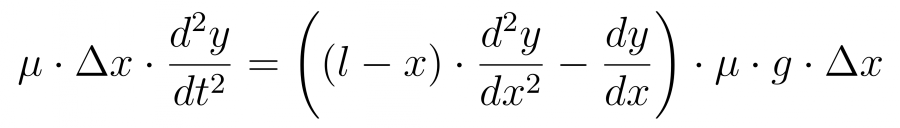
Сокращаем на dx и удельную массу.
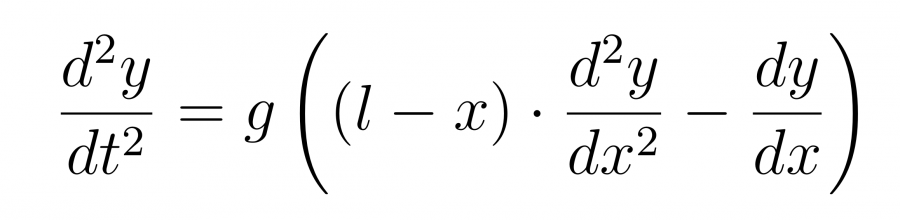
Заметим, что это уравнение не зависит от удельной массы, стало быть, все веревки и цепочки равной длины будут колебаться одинаково, независимо от массы. Для того, чтобы решить это уравнение, будем искать решение в виде
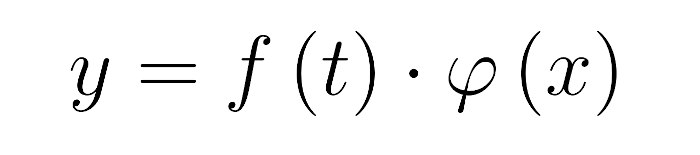
Подставив его в уравнение движения, получим
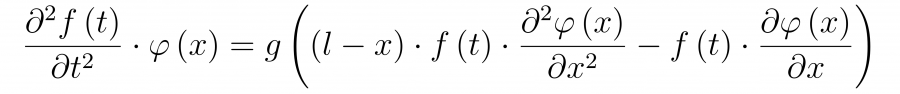
Разделив его на g и саму функцию, получим, что одна часть зависит только от времени, а другая только от X. Стало быть, их можно приравнять некоторой константе.
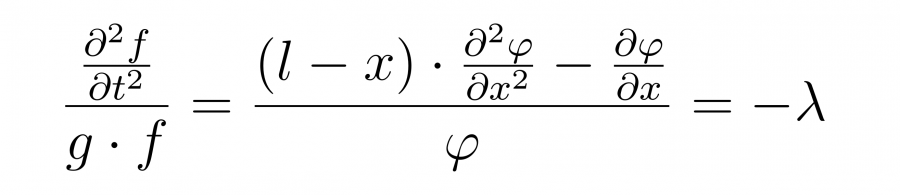
Рассмотрим сначала ту часть, которая зависит только от X
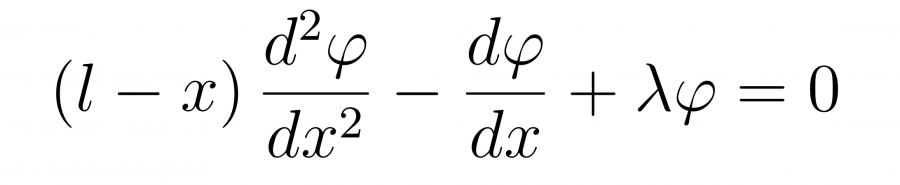
Чтобы решить это уравнение сделаем замену переменной
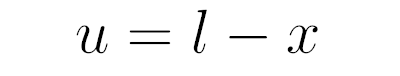
Тогда первая производная примет следующий вид
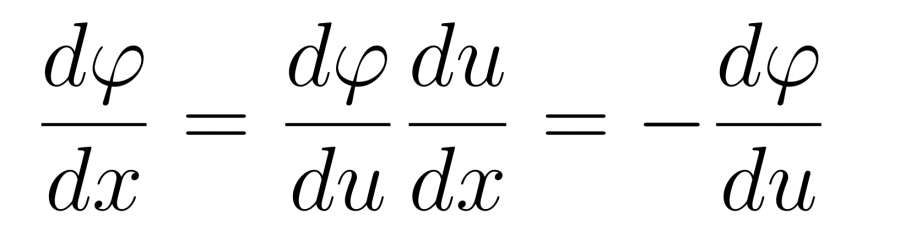
а вторая производная такой
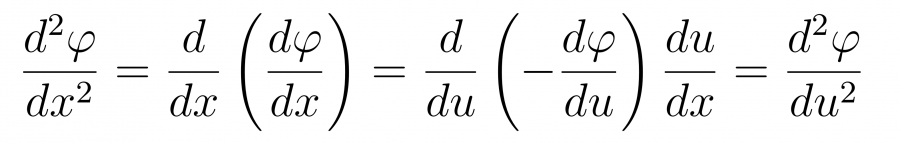
а уравнение перепишется в виде
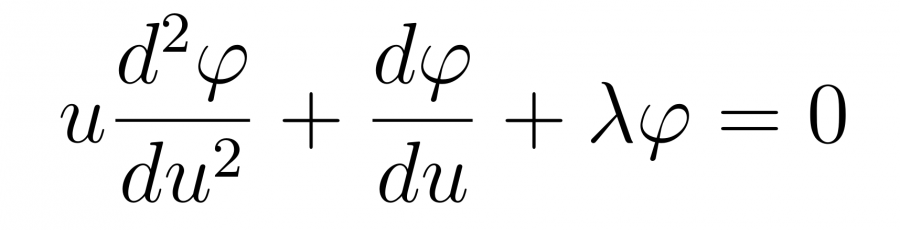
Нетрудно заметить, что это уравнение можно переписать в виде
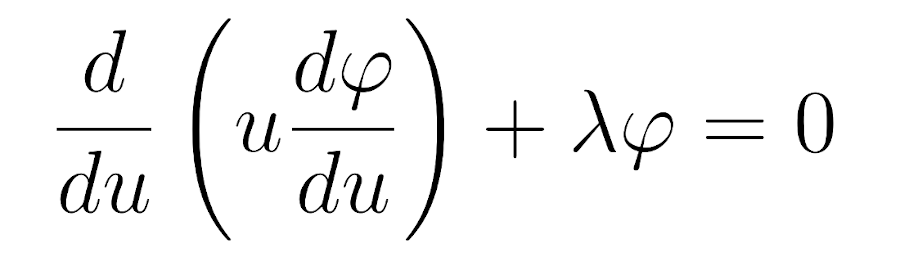
Поскольку пока непонятно, что это за уравнение, попробуем привести его к какому-нибудь известному дифференциальному уравнению.
Для этого сделаем замену
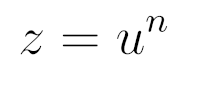
При этом первая производная примет следующий вид
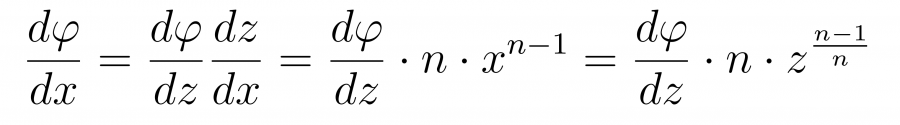
а само уравнение такой
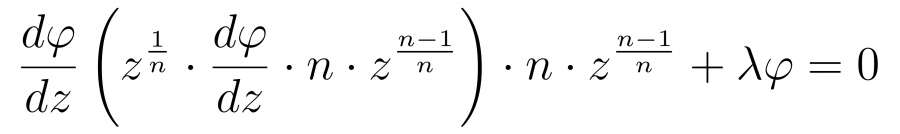
Выносим n в квадрате из под производной
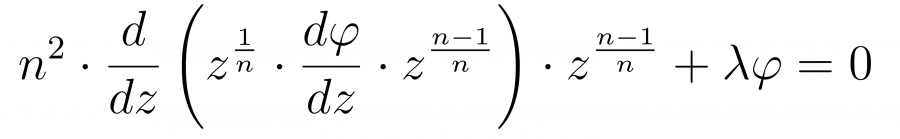
и сокращаем
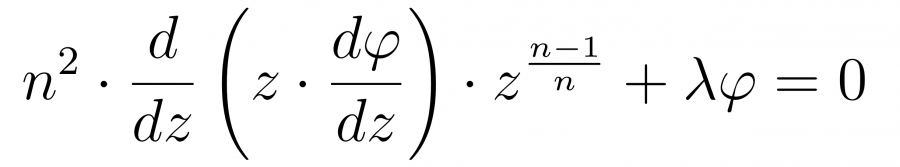
Производим дифференцирование и получаем следующее уравнение
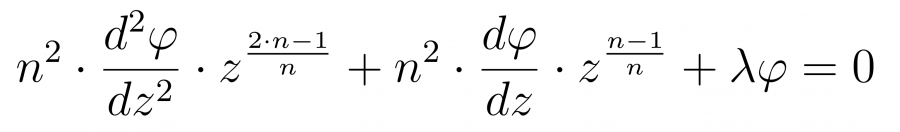
Подберем n таким образом, чтобы при старшей производной не было свободной переменной
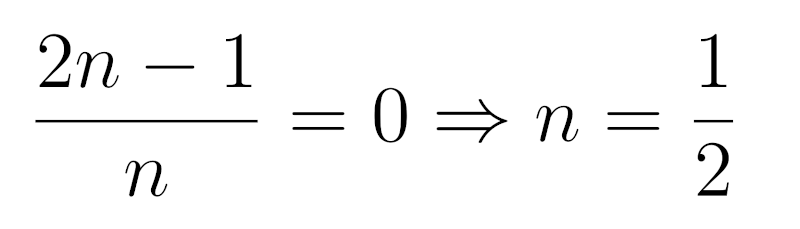
Получим следующее уравнение
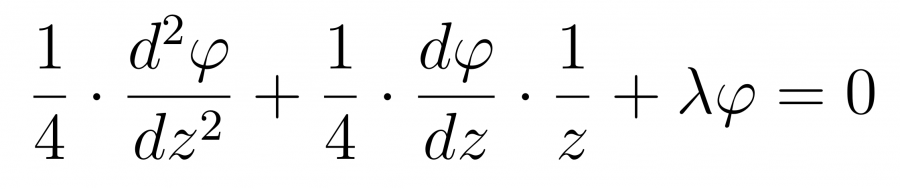
Домножаем на 4 и z в квадрате и получаем
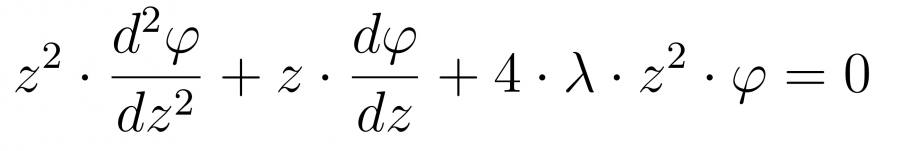
Это уже похоже на известное уравнение Бесселя, необходимо только избавиться от множителя у самой функции. Для этого делаем еще одно преобразование переменной
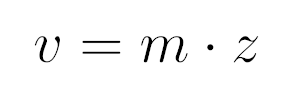
При этом первая производная станет равной
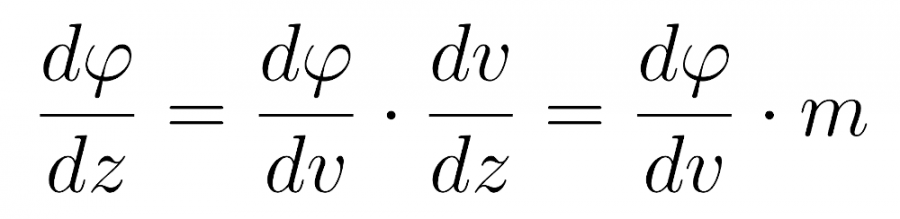
а вторая производная
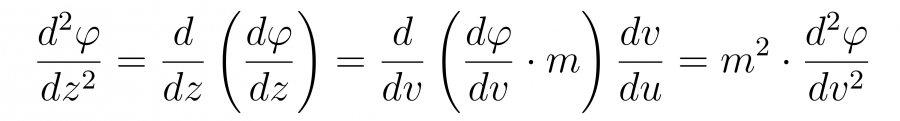
Подставляя в уравнение, получаем
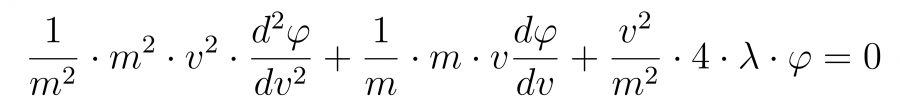
Если мы возьмем
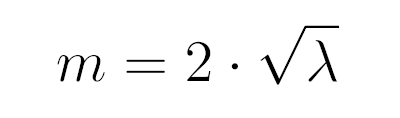
то получим уравнение Бесселя нулевого порядка
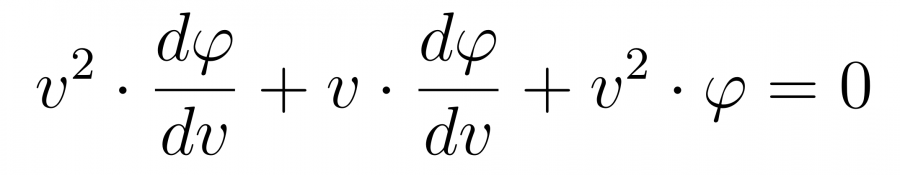
Решение такого уравнения имеет вид
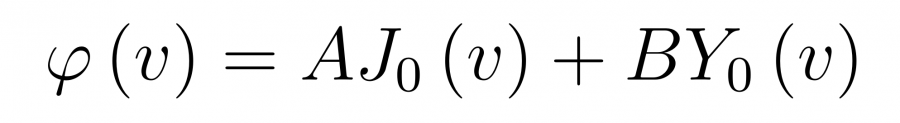
где A и B — константы, а J и Y — функции Бесселя нулевого порядка. Подставляя обратно переменную z, получим
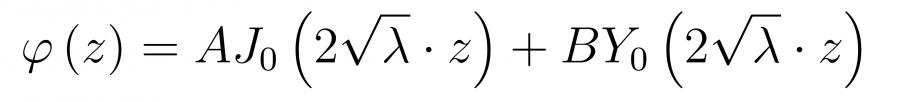
После подстановки переменной u, имеем следующе решение
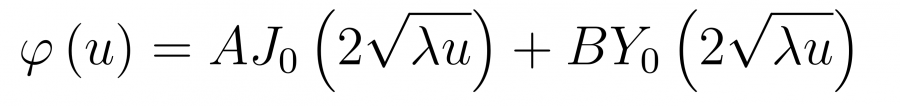
и, наконец, возвращаясь к переменной x, имеем
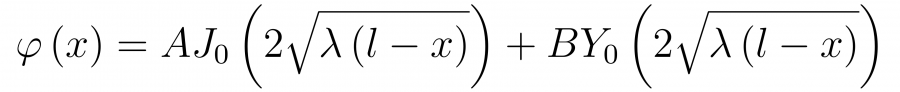
Используем тот факт, что наша функция должна быть конечной в точке x=l. Поскольку функция Y(x) бесконечна в нуле, B должно равняться нулю и наше решение будет иметь следующий вид
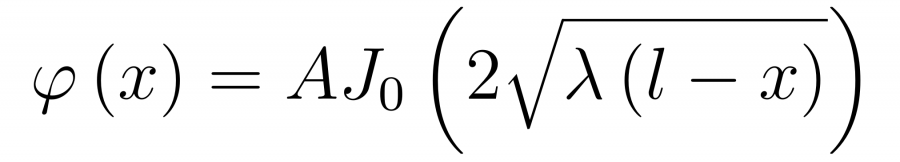
Теперь воспользуемся тем условием, что в точке подвеса значение нашей функции должно равняться нулю, то есть y(0)=0.
Из этого следует, что
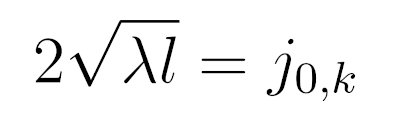
где j — нули функции Бесселя нулевого порядка. Отсюда можно определить значение лямбда
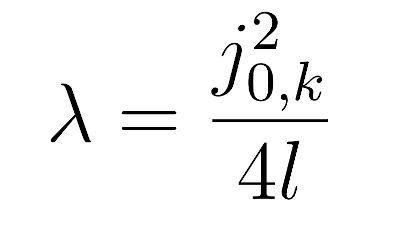
Подставляя лябда, получим
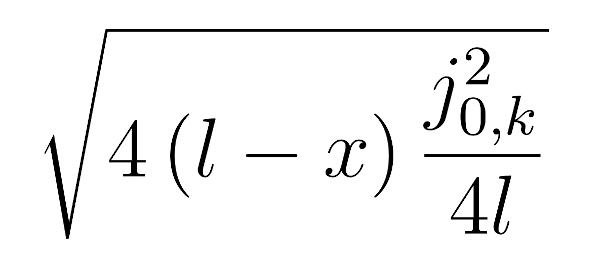
Что после сокращения дает собственные функции
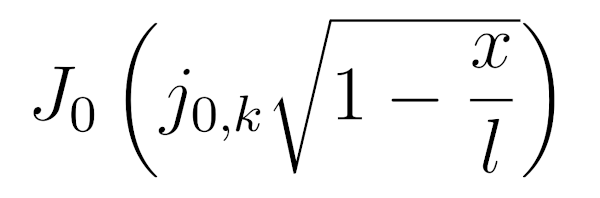
Дадим графики для первых пяти
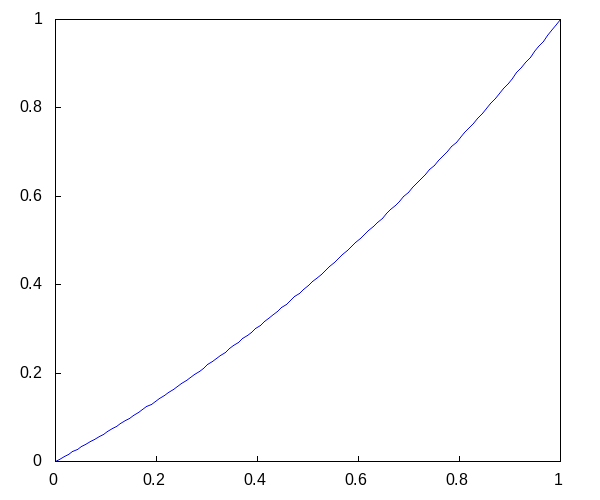
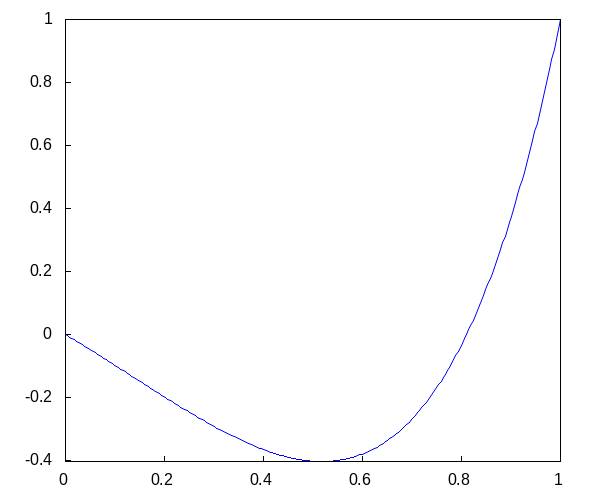
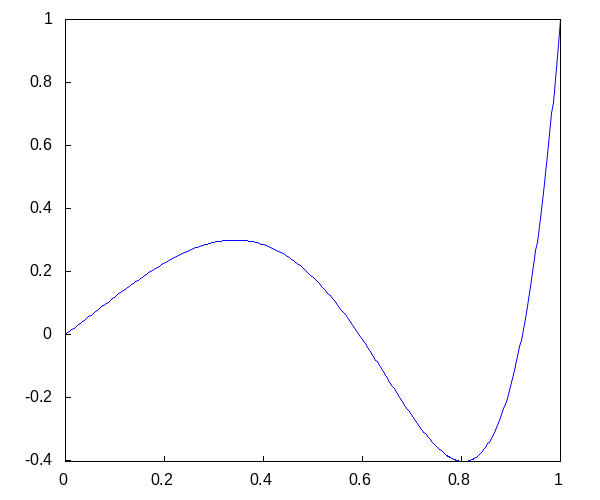
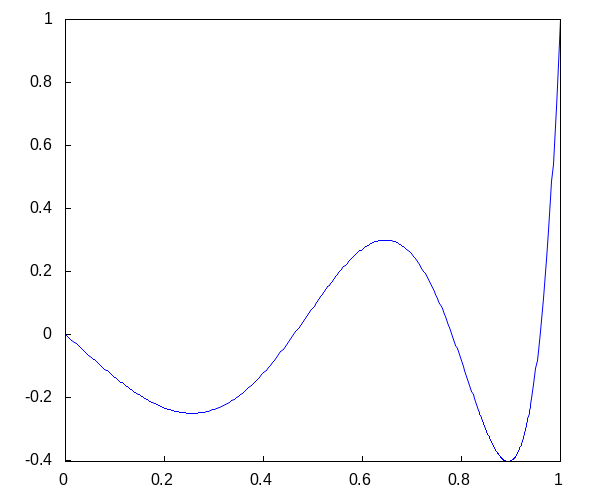
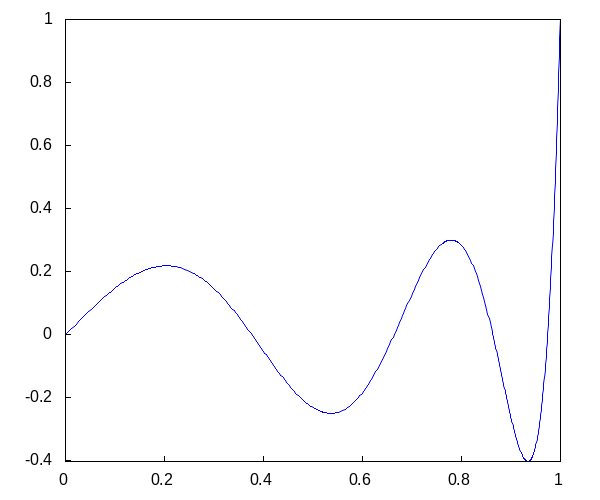
Вернемся теперь к той части начального уравнения, которая отвечает за зависимость от времени. Зная значения лямбда, можно вычислить собственные частоты
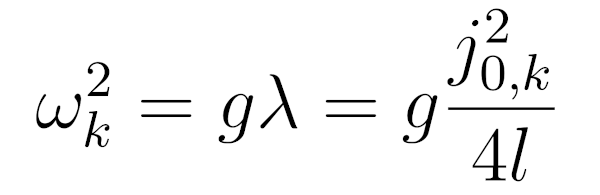
Извлекая корень, получим
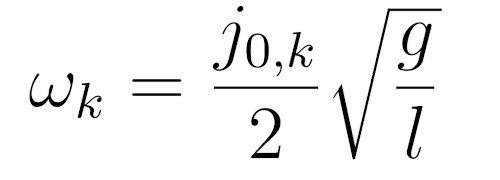
Соответствующие периоды будут равны
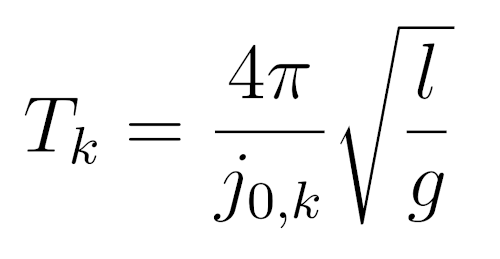
Сравните это выражение с периодом колебаний математического маятника.
На этом наше исследование колебаний свободно висящей цепочки окончено. Спасибо за внимание.
Автор: Андрей Плеханов





