RSA: от простых чисел до электронной подписи

Выясняем, как и откуда можно получить электронную подпись на примере криптосистемы RSA.

Введение

Наверняка вы сталкивались с таким понятием, как "электронная подпись". Если обратиться к федеральному закону, то можно найти следующее её определение:

«Электронная подпись - информация в электронной форме, которая присоединена к другой информации в электронной форме (подписываемой информации) или иным образом связана с такой информацией и которая используется для определения лица, подписывающего информацию»

Для меня, как для человека, редко работающего с подобного рода документами, определение несколько абстрактное, хоть и отражает суть ЭП - определение лица, подписавшего некоторый документ. Помимо этого, ЭП может быть использована для определения искажений переданного сообщения, в чём мы сможем убедиться позднее.

Задача ЭП ясна, теперь хотелось бы увидеть и прочувствовать, что именно скрывается за этими двумя словами. Копаясь дальше в гугле, можно найти довольно много различных алгоритмов создания цифровой подписи (DSA, ГОСТ Р 34.10-2012, RSA-PSS и т.д.), разбираться в которых неподготовленному пользователю сложно.

Спасти эту ситуацию и помочь разобраться в том, что есть ЭП, может криптосистема RSA, разработанная Ривестом, Шамиром и Адлеманом в 1978 году. Она не загромождена безумным количеством алгоритмов и основывается на относительно простой математике. В связи с этим можно шаг за шагом прийти от модульной арифметики к алгоритму создания электронной подписи, чему я и хочу посвятить данную статью.

Теорминимум

Сформируем небольшой словарик терминов, которые нам пригодятся далее:

• Открытый текст – данные, подлежащие шифрованию или полученные в результате расшифрования

• Шифртекст – данные, полученные в результате применения шифра к открытому тексту

• Шифр – совокупность обратимых преобразований, зависящая от некоторого параметра (ключа)

• Ключ – параметр шифра, определяющий выбор одного преобразования из совокупности.

• Факторизация – процесс разложения числа на простые множители.

• НОД – наибольший общий делитель.

• Числа a и b называются взаимно простыми, если НОД этих чисел равен 1.

• Функция Эйлера φ(n) – функция, равная количеству натуральных чисел, меньших n и взаимно простых с ним.

Хочу отметить, что на данном этапе подразумевается, что вы знакомы с арифметическими операциями по модулю. Если нет, то здесь можно о них почитать.

Как оно устроено

Прежде, чем окунуться в необъятный мир математики рассмотреть, как именно устроена RSA, обратимся к тому, как работают

Асимметричные криптосистемы

Рассмотрим задачу сохранности содержимого посылки при передаче от отправителя к адресату. Вот картинка с многим полюбившимся Алисой и Бобом:

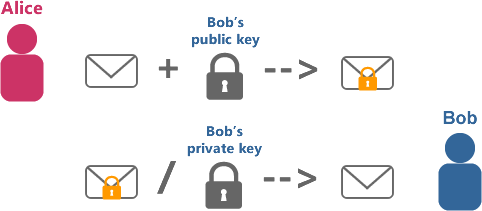
Алиса хочет передать Бобу посылку. Для начала Боб на своей стороне создает уникальные замок и ключ к нему (открытый и закрытый ключ соответственно). Далее, Боб делится с окружающим миром своим замком, чтобы любой желающий отправить ему посылку смог её закрыть. Поскольку ключ от подобного замка один и находится только у Боба, никто, кроме Боба, просмотреть содержимое после защёлкивания замка не сможет. В конце концов, Алиса с помощью полученного замка закрывает посылку и передаёт Бобу, который открывает её своим ключом. Таким образом устроены асимметричные криптографические системы, которой как раз является RSA.

В схеме передачи посылки все объекты вполне материальны. Однако сообщения, которые мы хотим шифровать, являются ничем иным, как последовательностью бит, которую нельзя "закрыть" на физический замок. Таким образом возникают вопросы: что такое ключ и замок? Как Бобу создать ключи? Каким образом ключи связаны и как с их помощью зашифровать сообщение? Здесь нам поможет математика.

Теперь к математике

Асимметричные криптографические системы основаны на так называемых односторонних функциях с секретом. Под односторонней понимается такая функция я y=f(x), которая легко вычисляется при имеющемся x, но аргумент x при заданном значении функции вычислить сложно. Аналогично, односторонней функцией с секретом называется функция y=f(x, k), которая легко вычисляется при заданном x, причём при заданном секрете k аргумент x по заданному y восстановить просто, а при неизвестном k – сложно.

Подобным свойством обладает операция возведения числа в степень по модулю:

Здесь φ(n) – функция Эйлера числа n. Пока условимся, что это работает, далее это будет доказано более строго. Теперь нужно понять, что из это является ключами Боба, а что сообщением. В нашем распоряжении имеются числа c, m, n, e, d.

Давайте посмотрим на первое выражение. Здесь число c получено в результате возведения в степень по модулю числа m. Назовём это действие шифрованием. Тогда становится очевидно, что m выступает в роли открытого текста, а c – шифртекста. Результат c зависит от степени e, в которую мы возводим m, и от модуля n, по которому мы получаем результат шифрования. Эту пару чисел (e, n) мы будем называть открытым ключом. Им Алиса будет шифровать сообщение.

Смотрим на второе действие. Здесь d является параметром, с помощью которого мы получаем исходный текст m из шифртекста c. Этот параметр мы назовём закрытым ключом и выдадим его Бобу, чтобы он смог расшифровать сообщение Алисы.

Что есть что разобрались, теперь перейдём к конкретике, а именно – генерации ключей Боба. Давайте выберем число n такое, что:

где p и q – некоторые разные простые числа. Для такого n функция Эйлера имеет вид:

Такой выбор n обусловлен следующим. Как вы могли заметить ранее, закрытый ключ d можно получить, зная открытый e. Зная числа p и q, вычислить функцию Эйлера не является вычислительно сложной задачей, ровно как и нахождение обратного элемента по модулю. Однако в открытом ключе указано именно число n. Таким образом, чтобы вычислить значение функции Эйлера от n (а затем получить закрытый ключ), необходимо решить задачу факторизации, которая является вычислительно сложной задачей для больших n (в современных системах, основанных на RSA, n имеет длину 2048 бит).

Возвращаемся к генерации ключей. Выберем целое число e:

Для него вычислим число d:

Для отыскания числа, обратного по модулю, можно воспользоваться алгоритмом Евклида.

Мы завершили с этапом генерации ключей. Теперь Боб публикует свой открытый ключ (e, n), прячет закрытый d, а мы переходим к Алисе.

Шифруем, дешифруем...

Возьмём в качестве сообщения число m (m ∈ [1, n − 1]). Чтобы Алисе зашифровать его, необходимо возвести его в степень e по модулю n. Эти числа идут вместе с открытым ключом Боба:

Здесь за с обозначен шифртекст, который Алиса будет должна передать Бобу. Отметим также, что c ∈ [1, n − 1], как и m. Расшифруем шифртекст, возведя его в степень закрытого ключа Боба d:

А теперь ответим на вопрос, почему m ≡ m′ . Ниже я приведу доказательство данного утверждения, но если оно (доказательство) вам не сильно интересно, то можете его пропустить и просто поверить, что это так.

Доказательство

Здесь нам понадобится теорема Эйлера:

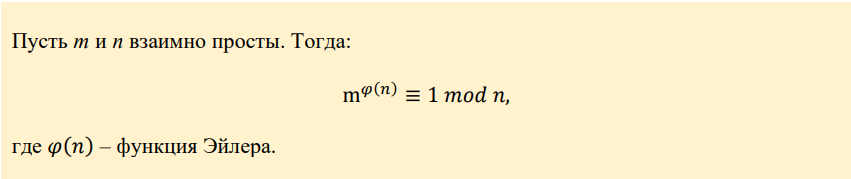
Также полезной будет китайская теорема об остатках:

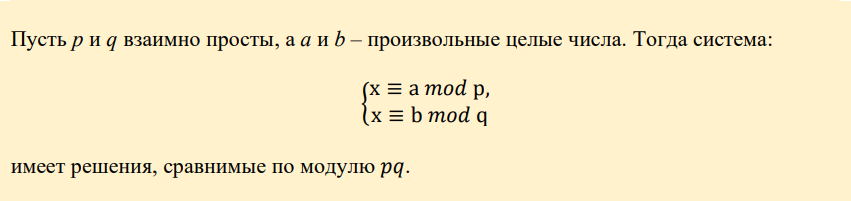
Теперь докажем, что m ≡ m′ :

Получаем подпись сообщения

Ещё раз напишем две ключевые формулы шифрования и расшифрования соответственно:

Теперь давайте предположим, что Боб хочет отправить Алисе открытку m от своего имени. У Боба в распоряжении уже имеются два ключа (e, n) и d, которые он сгенерировал по алгоритму, описанному ранее. Поскольку d является закрытым ключом, то можно им воспользоваться как уникальным идентификатором Боба. Давайте "зашифруем" m с помощью d:

Результат данной операции и есть подпись сообщения Боба. Заметим, что подпись напрямую зависит от подписываемого сообщения, а не только от того, что его подписывает Боб. Далее, Алиса получает сообщение m, подпись s и открытый ключ (e, n). По аналогии с расшифрованием, проверка подписи осуществляется возведением подписи s в степень открытой экспоненты e:

Если Алиса получила, что m ≡ m′, то подпись считается правильной.

Дочитавших до этого места хочу поздравить с получением первой цифровой подписи "на бумаге"!

Подпись документов

Рассмотренный алгоритм получения подписи изящен и прост в осознании, однако операция возведения в степень несколько "мешается". Наша текущая задача – подписать объёмный документ. Чтобы сэкономить время, мы не будем подписывать содержимое документа, а прибегнем к помощи хэш-функций (если вы не знаете, что такое хэш-функция, рекомендую почитать википедию). Скажу лишь то, что выходная последовательность хэш-функции имеет небольшую (по сравнению с размером ключей) длину, а также по имеющемуся хэшу нельзя однозначно восстановить исходные данные.

На картинках наглядно показано, в какой момент мы используем хэширование. Создание подписи:

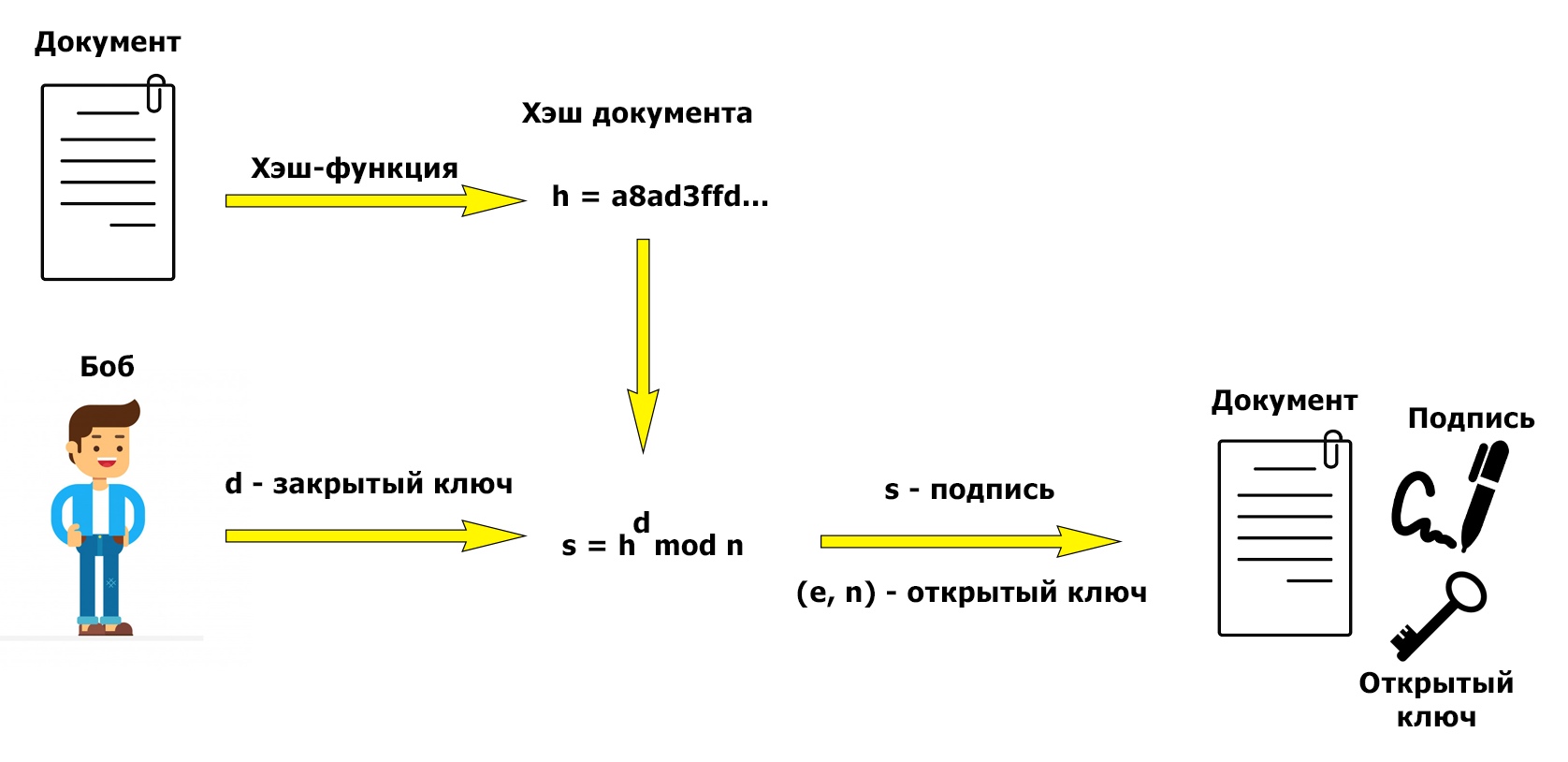
Проверка подписи:

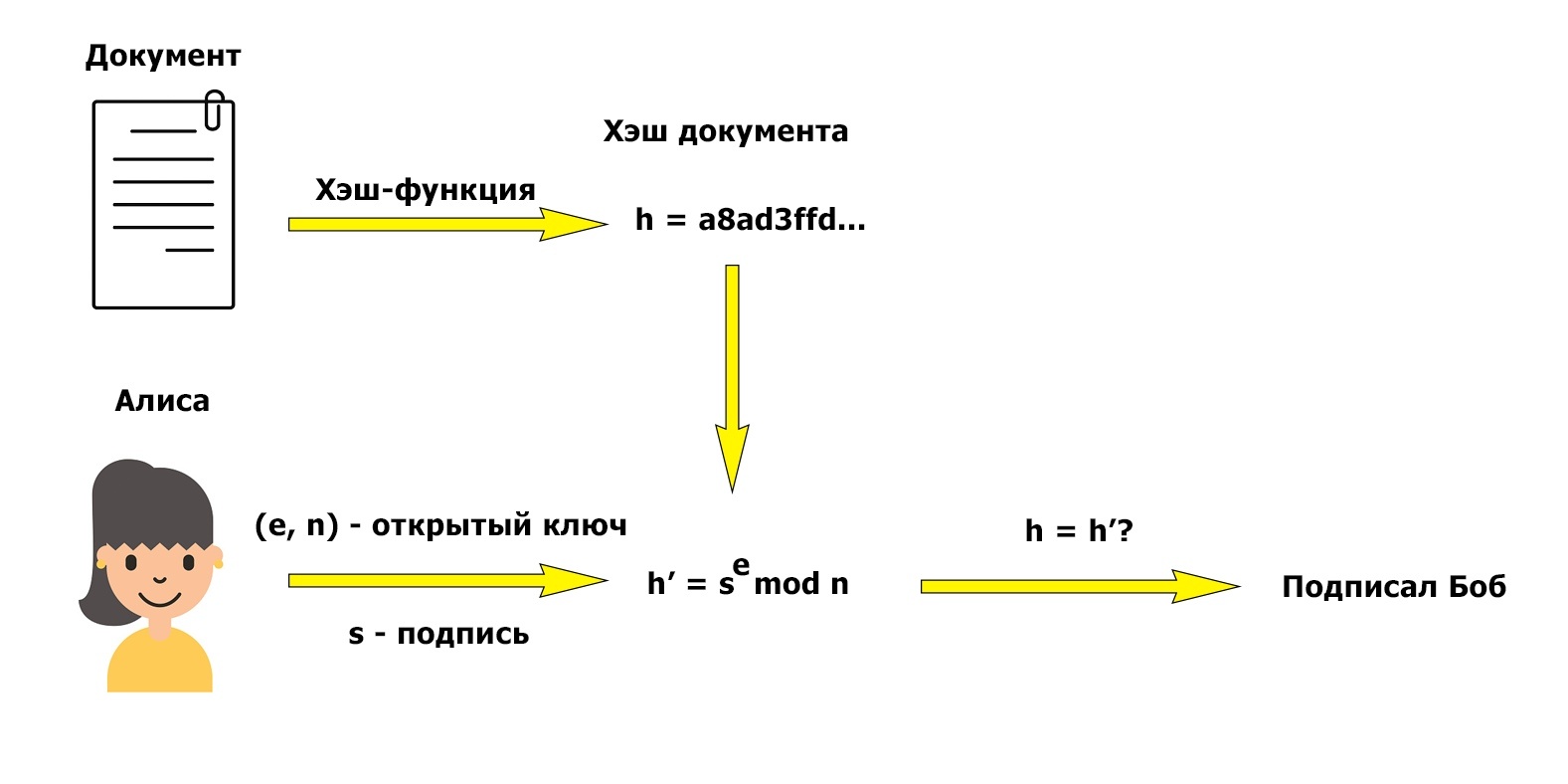
В качестве хэш-функции можно использовать SHA-256, как это сделано, например, в PGP. По теме практического создания электронной подписи с использованием PGP на хабре уже написана статья, поэтому на этом месте имеет смысл поставить точку и перейти к заключению.

Заключение

Вот мы и прошли все стадии создания электронной подписи, начиная с простой модульной арифметики и заканчивая, собственно, получением подписи. Обладая этими знаниями, вы можете попробовать перевести их на ваш любимый язык программирования и написать свою защищенную аську, например. В том, как именно их применить, вас ограничит только ваше воображение.

Отмечу, что другие существующие алгоритмы создания ЭП основаны на схожих принципах, поэтому надеюсь, что после прочтения этой статьи вам будет проще разобраться в них. "Следующей по сложности" я обозначу криптосистему Эль-Гамаля, но о ней уже не в этом посте.

Спасибо за внимание!

Источники

1. Handbook of Applied Cryptography by A. Menezes, P. van Oorschot and S. Vanstone

2. Криптографические методы защиты информации: учеб. пособие / С. М. Владимиров, Э. М. Габидулин, А. И. Колыбельников, А. С. Кшевецкий; под ред. А. В. Уривского. – М.: МФТИ, 2016

3. Маховенко Е. Б. Теоретико-числовые методы в криптографии — М.: Гелиос АРВ, 2006.

4. NIST Special Publication 800-57 Part 3 Revision 1

5. Молдовян Н.А. Теоретический минимум и алгоритмы цифровой подписи. – СПб.: БХВ-Петербург, 2010. - Учебное пособие

Автор: Егор

Источник