Главная

Ваши квадрокруги — неправильные

2020-09-03 в 9:38, admin, рубрики: squircle, графический дизайн, дизайн мобильных приложений, квадрат, квадрокруг, круг, математика, полярные координаты, сквиркл, суперэллипс

На днях вышла статья, посвящённая разнице между квадратом со скруглёнными краями и «квадрокругом» — промежуточной фигурой между окружностью и квадратом, полученной из формулы cуперэллипса. Мнения читателей разделились — не все увидели разницу, а кто увидели — не все отдали предпочтение «правильному» варианту. И я подозреваю, почему: эти ваши квадрокруги — ненастоящие!

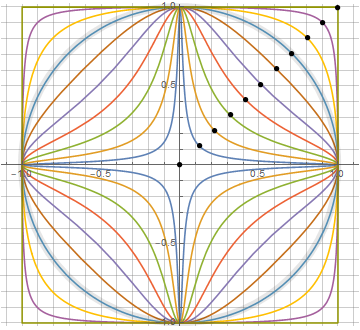
Альтернативное решение

Предпосылки

Некоторое время назад один мой близкий человек увлёкся рупоростроением и захотел построить рупор с круглым входом (для динамика), но прямоугольным выходом — из эстетических и практических соображений. Естественно, профиль должен перетекать из круга в квадрат достаточно плавно, чтобы не возникало излишних паразитных переотражений. Довольно быстро он нашёл формулу суперэллипса, однако результат его совершенно не вдохновил. При n от 1 до 2 углы были острыми, при n от 2 до бесконечности фигуры были больше похожи на квадраты со скруглёнными углами, чем на действительно промежуточные фигуры. И, поскольку квадрат получался лишь при стремлении n к бесконечности, совершенно непонятно было, на какой n останавливаться. 5? 10? 1000?

А ещё ему хотелось иметь формулу не параметрически заданную, а в полярных координатах.

В общем, он предложил мне подумать над альтернативным решением.

Моё решение (в полярных координатах) получилось таким:

$rho=sqrt{frac{2}{1+sqrt{1+left(frac{1}{k^4}-frac{2}{k^2}right) sin ^2(2 phi )}}}$

в которой параметр $k$ от 0 до 1 задаёт степень «оквадрачивания», причём линейно — определяя точку пересечения (k,k) фигуры с диагональю. Это значит, что можно однозначно определить наш квадрокруг через 3 точки. И да, при $k=1$ мы имеем самый настоящий квадрат, с прямыми сторонами и острыми углами. Ну а круг, соответственно, получается при $k=frac{1}{sqrt{2}}$ (косинус 45°). Варианты получаемых фигур отражены на КДПВ.

Вы также можете обратить внимание, что в этой формуле нет таких хитростей, как функции остатка от деления, взятия/отбрасывания знака и прочего — как это требуется для суперэллипса. Всё честно, только стандартные математические функции, с которыми не возникнет сложности при дифференцировании или интегрировании. Кстати про интегрирование — при желании, можно найти и площадь этих фигур (через эллиптические интегралы):

$frac{4 k^4 Eleft(frac{2 k^2-1}{k^4}right)-4 left(k^2-1right)^2 Kleft(frac{2 k^2-1}{k^4}right)}{2 k^2-1}$

Примечание

Эллиптические интегралы — это такие же функции, как и все остальные, вроде sin и cos. Похожее на операцию взятия первообразной название не должно вводить вас в заблуждение.

Развитие

Можно добавить больше вариативности полученным фигурам. Например, так:

$rho=sqrt{frac{1+sqrt{frac{(z-2)^2}{z^2}}}{1+sqrt{1+left(frac{1}{k^4}-frac{2}{k^2}right) sin^2(2phi)+left(frac{4(1-z)}{z^2}right)cos^2(2 phi)}}}$

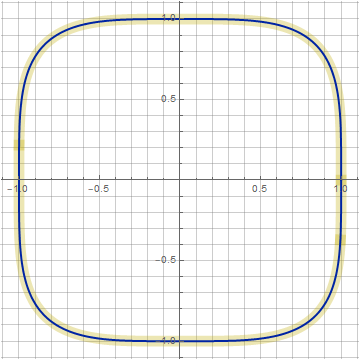
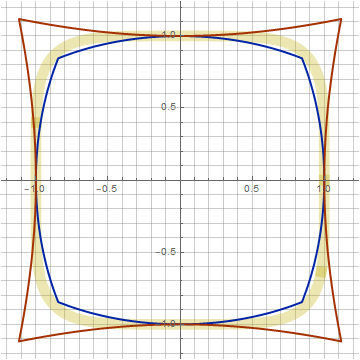
Здесь у нас появился ещё один параметр z, позволяющий искажать фигуру не нарушая идеологию построения. С её помощью можно приблизить нашу фигуру к суперэллипсу (на графиках отображён жёлтым цветом). Например, при n=4 (k=0.266, z=0.1) совпадение почти идеальное:

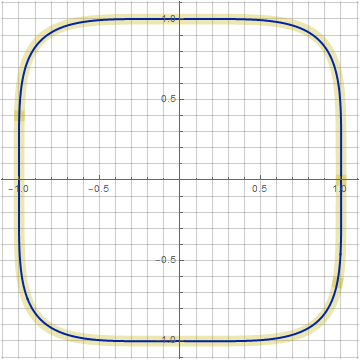
при более высоких n разница уже более ощутима (n=5, k=0.6, z=0.48):

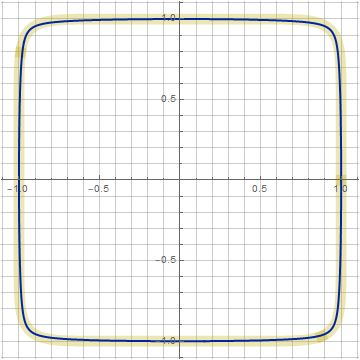
n=10, k=0.942, z=1.02:

И да, можно же пойти совсем радикальным способом! Такой дизайн иконок уж точно ни с чем не перепутаешь:

Ну и с анимацией тоже можно слегка пофантазировать:

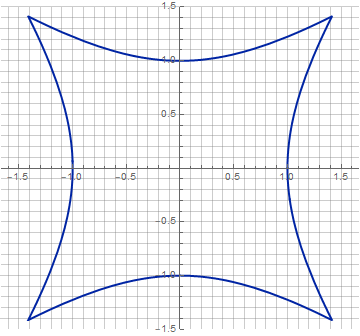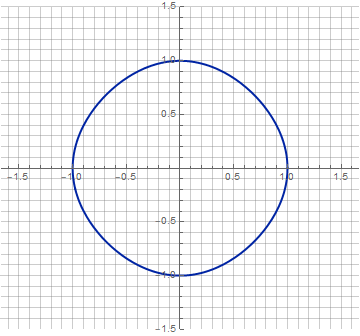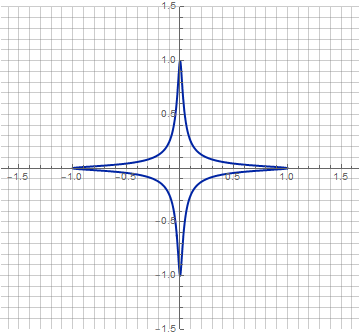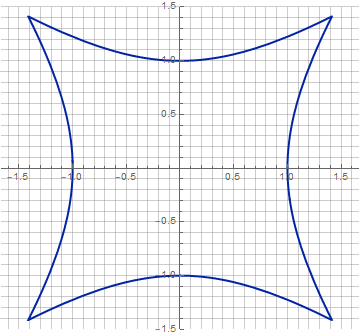
Заключение

Если некий дизайнер некоторой фирмы с (необязательно) фруктовым логотипом хочет получить уникальный дизайн, пусть и не отличающийся принципиально от уже существующих решений — возможно, стоит попробовать поискать ~~и запатентовать~~ действительно новую формулу, а не привлекать давно известное решение, навешивая на него тонны маркетингового булшита. Особенно если это может сделать just for fun простой человек из глубинки без специального образования.

P.S. Исходники статьи здесь.

Автор: Refridgerator

Источник