В настоящей статье предложен разработанный автором метод нечеткой индукции как объединение положений нечеткой математики и теории фракталов, введено понятие степени рекурсии нечеткого множества, представлено описание неполной рекурсии множества как его дробной размерности для моделирования предметной области. В качестве сферы применения предлагаемого метода и созданных на его основе моделей знаний как нечетких множеств рассмотрено управление жизненным циклом информационных систем, включая разработку сценариев использования и тестирования программного обеспечения.
Актуальность
В процессе проектирования и разработки, внедрения и эксплуатации информационных систем необходимо аккумулировать и систематизировать данные, сведения и информацию, которые собираются извне или возникают на каждом этапе жизненного цикла программного обеспечения. Это служит необходимой информационно-методической поддержкой проектных работ и принятия решений и особенно актуально в ситуациях высокой неопределенности и в слабоструктурированных средах. База знаний, формируемая в результате аккумуляции и систематизации подобных ресурсов, должна быть не только источником полезного опыта, полученного проектной группой в ходе работ по созданию информационной системы, но и максимально простым средством моделирования новых видения, способов и алгоритмов реализации проектных задач. Иными словами, такая база знаний является хранилищем интеллектуального капитала и, вместе с тем, инструментом управления знаниями [3, 10].
Эффективность, полезность, качество базы знаний как инструмента коррелируют с ресурсоемкостью ее ведения и результативностью извлечения знаний. Чем проще и быстрее сбор и фиксация знаний в базе и чем более пертинентны результаты запросов к ней, тем лучше и надежнее сам инструмент [1, 2]. Тем не менее, дискретные методы и средства структуризации, которые применимы для систем управления базами данных, в том числе нормализация отношений реляционных баз данных, не позволяют описывать или моделировать смысловые компоненты, интерпретации, интервальные и непрерывные семантические множества [4, 7, 10]. Для этого нужен методологический подход, обобщающий частные случаи конечных онтологий и приближающий модель знаний к непрерывности описания предметной области информационной системы.
Таким подходом может быть объединение положений теории нечеткой математики и понятия фрактальной размерности [3, 6]. Оптимизируя описание знаний по критерию степени непрерывности (величине шага дискретизации описания) в условиях ограничения по принципу неполноты Гёделя (в информационной системе – принципиальной неполноты рассуждений, знаний, выводимых из этой системы при условии ее непротиворечивости), выполняя последовательную фаззификацию (приведение к нечеткости), получаем формализованное описание, которое максимально полно и связно отображает некоторый массив знаний и с которым при этом можно выполнять любые операции информационных процессов – сбор, хранение, обработку и передачу [5, 8, 9].
Определение рекурсии нечеткого множества
Пусть X – множество значений некоторой характеристики моделируемой системы:
(1)
где n = [N ≥ 3] – количество значений такой характеристики (больше, чем элементарный набор (0; 1) – (ложь; истина)).
Пусть X = B, где B = {a,b,c,...,z} – множество эквивалентов, поэлементно соответствующее множеству значений характеристики X.
Тогда нечеткое множество 
, которое соответствует нечеткому (в общем случае) понятию, описывающему характеристику X, может быть представлено в виде:
(2)
где m – шаг дискретизации описания, i принадлежит N – кратность шага.
Соответственно, чтобы оптимизировать модель знаний об информационной системе по критерию непрерывности (мягкости) описания, оставаясь в границах пространства неполноты рассуждений, введем степень рекурсии нечеткого множества 
и получим следующий вариант его представления:
(3)
где 
– множество, соответствующее нечеткому понятию, в общем случае более полно описывающему характеристику X, чем множество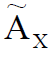 
, по критерию мягкости; Re – степень рекурсии описания.
Следует учесть, что 
(сводимо к четкому множеству) в частном случае при необходимости.
Введение дробной размерности
При Re = 1 множество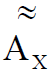 
представляет собой обычное нечеткое множество 2-й степени, включающее в качестве элементов нечеткие множества (либо их четкие отображения), описывающие все значения характеристики X [1, 2]:
(4)
Однако это – вырожденный случай, и в наиболее полном представлении часть элементов 
могут быть множествами, в то время как остальные – тривиальными (предельно простыми) объектами. Поэтому для определения такого множества необходимо ввести дробную рекурсию – аналог дробной размерности пространства (в данном контексте – пространства онтологии некоторой предметной области) [3, 9].
При Re дробной получаем следующую запись 
:
(5)
где 
– нечеткое множество для значения X1, 
– нечеткое множество для значения X2 и т. д.
В таком случае рекурсия становится по сути фрактальной, а множества описаний – самоподобными.
Определение множества функциональных возможностей модуля
Архитектура открытой информационной системы предполагает принцип модульности, который обеспечивает возможность масштабирования, репликации, адаптивность и эмерджентность системы. Модульное построение позволяет максимально приблизить технологическую реализацию информационных процессов к их естественному объективному воплощению в реальном мире, разрабатывать наиболее удобные по своим функциональным свойствам средства, призванные не заменять людей, а эффективно помогать им в управлении знаниями.
Модуль представляет собой некую обособленную сущность информационной системы, которая может быть обязательной или опциональной для целей существования системы, но в любом случае обеспечивает уникальный в границах системы набор функций.
Все многообразие функциональных возможностей модулей можно описать тремя типами операций: создание (запись новых данных), редактирование (изменение ранее записанных данных), удаление (стирание ранее записанных данных).
Пусть X – некая характеристика таких функциональных возможностей, тогда соответствующее множество X можно представить в виде:
(6)
где X1 – создание, X2 – редактирование, X3 – удаление,
(7)
При этом функциональные возможности любого модуля таковы, что создание данных не самоподобно (реализовано без рекурсии – функция создания не повторяет саму себя), а редактирование и удаление в общем случае могут предусматривать как поэлементную реализацию (выполнение операции над избранными элементами множеств данных), так и сами включать в составе подобные себе операции.
Следует отметить, что если операция для функциональной возможности X в данном модуле не выполняется (не реализована в системе), то соответствующее такой операции множество рассматривается как пустое.
Таким образом, для описания нечеткого понятия (высказывания) «модуль позволяет выполнить операцию с соответствующим набором данных в целях информационной системы» нечеткое множество 
в простейшем случае можно представить как:
(8)
Такое множество в общем случае имеет степень рекурсии равную 1,6(6) и является фрактальным и нечетким одновременно.
Подготовка сценариев использования и тестирования модуля
На этапах разработки и эксплуатации информационной системы необходимы специальные сценарии, описывающие порядок и содержание операций для использования модулей по их функциональному назначению (сценарии использования, англ. use-case), а также для проверки соответствия ожидаемого и реального результатов работы модулей (сценарии тестирования, англ. test-case).
С учетом представлений, изложенных выше, процесс работы над такими сценариями можно описать следующим образом.
Для модуля формируется нечеткое множество 
:
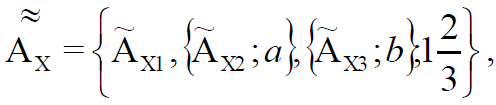(9)
где
– нечеткое множество для операции создания данных по функциональной возможности X;
– нечеткое множество для операции редактирования данных по функциональной возможности X, при этом степень рекурсии a (вложения функции) является натуральным числом и в тривиальном случае равна 1;
– нечеткое множество для операции удаления данных по функциональной возможности X, при этом степень рекурсии b (вложения функции) является натуральным числом и в тривиальном случае равна 1.
Такое множество описывает, что именно (какие объекты данных) создают, редактируют и/или удаляют при любом варианте использования модуля.
Затем составляется набор сценариев использования Ux по функциональной возможности X для рассматриваемого модуля, в каждом из которых описывается, для чего (для какой бизнес-задачи) создают, редактируют и/или удаляют объекты данных, описанные множеством 
, и в каком порядке:
(10)
где n – количество сценариев использования для X.
Далее составляют набор сценариев тестирования Tx по функциональной возможности X для каждого сценария использования рассматриваемого модуля. В сценарии тестирования описывается, какие значения данных и в каком порядке используются при выполнении сценария использования, а также какой результат должен быть получен:
(11)
где [D] – массив тестовых данных, n – количество сценариев тестирования для X.
В описанном подходе количество сценариев тестирования равно числу соответствующих сценариев использования, что позволяет упростить работу над их описанием и актуализацией по мере развития системы. Кроме того, такой алгоритм может быть использован для автоматизации тестирования программных модулей информационной системы.
Заключение
Представленный метод нечеткой индукции может быть имплементирован на разных стадиях жизненного цикла любой модульной информационной системы как в целях накопления описательной части базы знаний, так и в работе над сценариями использования и тестирования модулей.
Более того, нечеткая индукция помогает синтезировать знания на основе полученных нечетких описаний подобно «когнитивному калейдоскопу», в котором часть элементов остаются четкими и однозначными, в то время как другие по правилу самоподобия применяются указанное в степени рекурсии количество раз для каждого множества известных данных. В совокупности полученные нечеткие множества формируют модель, которая может быть использована как для целей информационной системы, так в интересах поиска новых знаний вообще.
Подобного рода методология может быть отнесена к своеобразной форме «искусственного интеллекта» с учетом того, что синтезированные множества не должны противоречить принципу неполноты рассуждений и призваны помогать интеллекту человека, а не заменять его.
Список литературы
- Борисов В.В., Федулов А.С., Зернов М.М., «Основы теории нечетких множеств». М.: Горячая линия – Телеком, 2014. – 88 с.
- Борисов В.В., Федулов А.С., Зернов М.М., «Основы теории нечеткого логического вывода». М.: Горячая линия – Телеком, 2014. – 122 с.
- Деменок С.Л., «Фрактал: между мифом и ремеслом». Спб: Академия исследования культуры, 2011. – 296 с.
- Заде Л., «Основы нового подхода к анализу сложных систем и процессов принятия решений» / «Математика сегодня». М.: «Знание», 1974. – С. 5 – 49.
- Кранц С., «Изменчивая природа математического доказательства». М.: Лаборатория знаний, 2016. – 320 с.
- Маврикиди Ф.И., «Фрактальная математика и природа перемен» / «Дельфис», №54 (2/2008), http://www.delphis.ru/journal/article/fraktalnaya-matematika-i-priroda-peremen.
- Мандельброт Б., «Фрактальная геометрия природы». М.: Институт компьютерных исследований, 2002. – 656 с.
- «Основы теории нечетких множеств: Методические указания», сост. Коробова И.Л., Дьяков И.А. Тамбов: Изд-во Тамб. гос. тех. Ун-та, 2003. – 24 с.
- Успенский В.А., «Апология математики». М.: Альпина Нон-фикшн, 2017. – 622 с.
- Zimmerman H. J. «Fuzzy Set Theory – and its Applications», 4th edition. Springer Seience + Business Media, New York, 2001. – 514 p.
Автор: Дмитрий Кочергов
