Коды Грея имеют близкую родственную связь с кривой Гильберта.
Впрочем, при общении с коллегами выяснилось, что эта несложная зависимость выглядит в их глазах как нечто нетривиальное. Поиск в интернетах навскидку ничего не дал кроме мутной фразы в вики: “кривые Гильберта в пространствах большей размерности являются представителями обобщений кодов Грея”. Поэтому возникло желание раскрыть тему — коротенько, простым языком.
В результате под катом — «скандалы, интриги, расследования».
Основная особенность кода Грея — два соседних в лексикографическом порядке значения отличаются только в одном разряде. С другой стороны, кривая Гильберта непрерывна — расстояние между двумя соседними точками всегда единица. Уже только одно это намекает об их внутренней связи.
Код Грея описывает похождения кривой Гильберта в рамках единичного гиперкуба. В самом деле, если взять 3-разрядный код и нарисовать его в 3-мерном пространстве (принимая каждый разряд за соответствующую координату), получим
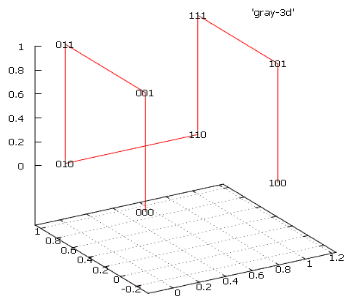
Фиг.1 3-разрядный код Грея как 3-мерный куб
Знакомая картина — это 3-мерный симплекс кривой Гильберта! Последовательно заменяя каждый узел симплекса на такой же симплекс (с учетом поворотов и отражений для сохранения непрерывности), получим кривую Гильберта 4х4х4.
Продолжая эти итерации, сможем непрерывно заполнить кубическую решетку любого размера.

Фиг.2 несколько итераций симплекса кривой Гильберта.
Но как так получилось?
Известно, что код Грея самоподобен. Его иногда называют зеркальным “из-за того, что первая половина значений при изменении порядка эквивалентна второй половине, за исключением старшего бита. Старший бит просто инвертируется”. Для наглядности, 3-разрядный код — самый старший разряд — самый левый:
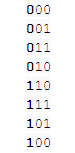
Раз уж речь зашла о самоподобии, начнём с начала — с одноразрядного кода. Строго говоря, можно было бы начать и с нулевой размерности — точки, принципиально это ничего не меняет, просто слов пришлось бы написать больше.
Одноразрядный код Грея даже проще, чем трёхлинейная винтовка, он либо 0, либо 1. Геометрически это соответствует одномерному единичному кубу — отрезку. По отрезку можно двигаться либо из начала в конец, либо из конца в начало — с точностью до симметрии это одно и то же. Но всё же, началом будем называть то место, где значение меньше (вспомним, что стороны куба это разряды числа), а концом — где больше.
Перейдём к двумерному случаю. Двумерный куб — квадрат. Принимая во внимание самоподобие, мы клонируем одномерный куб (0,1) и получаем два отрезка — (0,0 -> 1,0) и (0,1 -> 1,1). Теперь требуется соединить эти отрезки, чтобы получить обход квадрата. И здесь возникаю два варианта:
- соединяем начало предыдущей итерации — одномерного куба с началом его клона. С точностью до симметрии это тоже самое, что и соединение конца с концом. Тип симметрии — зеркальная. Этот вариант условно назовём “миссионерским”.
- соединяем конец предыдущей итерации с началом его клона. С точностью до симметрии это тоже самое, что и соединение начала отрезка с концом клона. Тип симметрии — центральная. Назовём этот вариант “паровозиком”.
Аналогично действуем при переходе к трёх и более мерным случаям.

Фиг.3 Первые две итерации “миссионерского” варианта
Здесь красным цветом выделена предыдущая итерация, синим — её клон, бирюзовым — их соединение.
Обратим внимание — соединение всегда проходит по единственной размерности — вновь добавленной, отсюда в силу самоподобия и появляется основная особенность кода Грея. А раз соединяется конец предыдущей итерации с концом её клона, возникает “зеркальность” — при обходе, клон мы вынуждены проходить в обратном порядке. Вне зависимости от размерности. Здесь же видно происхождение и особенности кривой Гильберта — как бы ни была велика решетка (любой размерности), на низовом уровне это всё тот же единичный куб с переходами длиной в единицу.

Фиг.4 Первые две итерации варианта “паровозик”, те же цвета
А ведь и эта музыка нам знакома — получился симплекс Z-кривой. Слово симплекс здесь также означает, что если взять каждую его точку и заменить на симплекс, получим куб 4х4х4, продолжая итерации — можно заполнить сколь угодно большую кубическую решетку.
Забавно, что в этом случае преобразование пройденного от начала координат пути в код, который может быть разобран на разряды-координаты тривиально.
Тогда как случае кода Грея это G = W ^ (W >> 1), где W-пройденная длина, G — код Грея.

Фиг.5 первые две итерации Z-кривой (wiki)

Фиг.6 для сравнения, первые две итерации кривой Гильберта (wiki)
А ведь других то (естественных) вариантов обхода единичного гиперкуба и нет.
Вот и получается, что куда ни кинь, кругом Гильберт, Лебег … и пустота.
PS: на титульной картинке круговой энкодер с восьмиразрядным кодом Грея.
PPS: тут меня поправляют, что симплекс — вполне устоявшийся термин, нехорошо с ним так. Что-же, в данной статье ведь не просто симплекс, а симплекс кривой Гильберта или симплекс Z-кривой. Пусть правоверные математики меня простят.
Автор: Борис Муратшин