Алексей Савватеев: Теоретико-игровая модель социального раскола (+ опрос по nginx)

Привет!
Меня зовут Ася. Нашла очень крутую лекцию, не могу не поделиться.

Предлагаю вашему вниманию конспект видеолекции о социальных конфликтах на языке математиков-теоретиков. Полная лекция доступна по ссылке: Модель социального раскола: игра тернарного выбора на сетях взаимодействия (А. В. Леонидов, А. В. Савватеев, А. Г. Семёнов). 2016.

Алексей Владимирович Савватееев — кандидат экономических наук, доктор физико-математических наук, профессор МФТИ, ведущий научный сотрудник РЭШ.

В данной лекции я расскажу о том, как математики и теоретики-игровики смотрят на повторяющийся социальный феномен, примерами которого являются голосование за выход Англии из Евросоюза (англ. Brexit), явление глубокого социального раскола в России после Майдана, выборы в США с сенсационным исходом. 

Как можно смоделировать подобные ситуации, чтобы в них были отголоски реальности? Чтобы понять феномен, необходимо изучать его всесторонне, но в этой лекции будет модель.

Социальный раскол означает

В этих трех сценариях общее то, что человек так или иначе примыкает к какому-то лагерю, либо же отказывается участвовать и обсуждать свой выбор. Т.е. Выбор каждого человека тернарный — из трех значений: 

• 0 — отказаться от участия в конфликте;
• 1 — участвовать в конфликте на одной стороне; 
• -1 — участвовать в конфликте на противоположной стороне.

Есть прямые последствия, которые связаны с Вашим собственным отношением к конфликту на самом деле. Есть предположение, что каждый человек имеет какое-то априорное ощущение того, кто здесь прав. И это вещественная переменная. 

К примеру, когда человек действительно не понимает, кто прав, точка располагается на числовой прямой где-то около нуля, к примеру на 0,1. Когда человек на 100% уверен, что кто-то прав, то его внутренний параметр будет уже -3 или +15, в зависимости от силы убеждений. Т. е. существует некий вещественный параметр, который у человека в голове есть, и он выражает его отношение к конфликту.

Важно, если вы выбираете 0, то это никаких последствий для Вас не влечет, в игре нет выигрыша, Вы отказались от конфликта.

Если Вы выбираете что-то не созвучное с Вашей позицией, то перед vi появится минус, к примеру v_i= — 3. Если Ваша внутренняя позиция совпадает с той стороной конфликта, на которой Вы выступаете, и Ваша позиция σ_i=-1, то v_i= +3. 

Тогда возникает вопрос, по каким причинам иногда приходится выбирать не ту сторону, что у Вас в душе? Это может происходить под давлением Вашего социального окружения. И это есть постулат.

Постулат состоит в том, что на Вас оказывают влияние последствия, от Вас не зависящие. Выражение a_ji — это вещественный параметр степени и знака влияния на Вас со стороны j.  Вы это номер i, а человек, который на Вас влияет, это человек номер j. Потом будет целая матрица таких a_ji. 

Этот человек j может даже влиять на Вас отрицательно. К примеру, так можно описать  выступление неприятного Вам политического деятеля на противоположной Вам стороне конфликта. Когда Вы смотрите на выступление, и думаете: «Этот идиот, и смотрите, что он говорит, я же говорил, что он идиот». 

Однако, если рассматривать влияние близкого или уважаемого Вами человека, то оно оказывается сразу одним игроком j на всех игроков i. И это влияние домножается на совпадение, или несовпадение принятых позиций. 

Т.е. если σ_i, σ_j, положительного знака, и при этом a_ji тоже положительного знака, то это плюс к Вашей функции выигрыша. Если же Вы или человек, который Вам очень важен, приняли нулевую позицию, то этого слагаемого нет.  

Таким образом мы попытались учесть все эффекты социального влияния.

Далее следующий момент. Таких моделей социального взаимодействия, описанных с разных сторон (модели принятия порогового решения, много иностранных моделей), существует много. В них рассматривают стандартную для теории игр концепцию, которая называется равновесие Нэша. Есть глубокая неудовлетворенность этой концепцией для игр с большим числом участников, как в примерах с Великобританией и США, упомянутых выше, т. е. много миллионов людей.   

В этой ситуации правильное решение задачи проходит через приближение с помощью континуума. Количество игроков — это какой-то континуум, «облако», играющее, при неком пространстве важных параметров. Есть теория континуальных игр, Ллойда Шепли

«Значение для не атомических игр». Это подход к кооперативной теории игр. 

Некооперативной теории игр с континуальным количеством участников, как теории пока нет. Существуют отдельные классы, которые изучаются, но в общую теорию эти знания пока не сформированы. И одна из основных причин ее отсутствия в том, что в конкретном случае равновесие Нэша неправильно. По сути неправильная концепция. 

Что же тогда правильная концепция? В последние несколько лет есть некое согласие, что концепция, разработанная в работах Палфри и Маккелви, которая звучит на английском как "Quantal response equilibrium", или "Равновесие дискретного отклика", как ее перевели мы с Захаровым. Перевод принадлежит нам, и так как до нас ее никто не переводил на русский язык, мы навязали этот перевод русскоязычному миру.

Мы имели в виду под этим названием то, что каждый конкретный человек не играет смешанную стратегию, он играет чистую. Но в этом «облаке» возникают зоны, в которых выбирается та или иная чистая, и в ответ, я вижу, как человек играет, но не знаю, где он в этом облаке находится, т. е. там скрытая информация есть, я воспринимаю человека в «облаке» как вероятность, с которой он пойдет тем или иным образом. Это статфизическая концепция. Взаимообогащающий симбиоз физиков и теоретиков игроков, как мне кажется, определит теорию игр 21 века. 

Мы обобщаем имеющийся опыт моделирования таких ситуаций с совершенно произвольными начальными данными и выписываем систему уравнений, которая отстоится к равновесию дискретного отклика. На этом все, далее, чтобы решить уравнения, необходимо сделать разумную аппроксимацию ситуаций. Но это все пока впереди, это огромное направление в науке.

Равновесие дискретного отклика — это равновесие, в котором, на самом деле, мы играем непонятно с кем. При этом к выигрышу от чистой стратегии добавляется ε. Есть три выигрыша, каких-то три числа, которые означают «топить» за одну сторону, «топить» за другую сторону и воздержаться, и есть ε, которая прибавляется к этим трём. При этом комбинация этих ε неизвестна. Комбинацию можно оценить лишь априорно, зная вероятность распределения для ε. При этом вероятности комбинации ε должны диктоваться собственными выборами человека, т. е. его оценками других людей и оценками их вероятностей. Эта взаимосогласованность и есть равновесие дискретного отклика. Мы еще вернемся к этому моменту.

Формализация через равновесие дискретного отклика

Вот как выглядит выигрыш в данной модели:

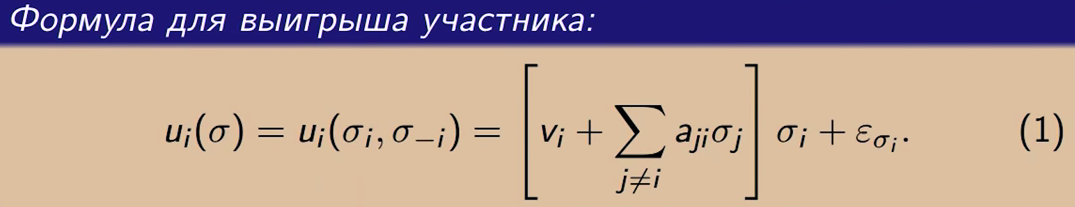
Она собирает в скобку все влияние, которое оказывается на Вас, если Вы выбрали какую-то сторону, либо будет домножаться на ноль, если никакую сторону не выбрали. Далее оно будет со знаком «+», если σ₁ = 1, и со знаком «-», если σ₁ = -1. И к этому добавляется ε. Т. е. σ_i домножается на Ваше внутреннее состояние, и всех людей, которые на Вас влияют. 

При этом, какой-то конкретный человек может влиять на миллионы людей, как влияют на миллионы людей медийные личности, актеры или даже президент. Получается, матрица влияния ужасно несимметричная, по вертикали она может содержать огромное количество ненулевых вхождений, а по горизонтали, из 200 млн человек в стране, к примеру, 100 ненулевых чисел. У каждого этот выигрыш — сумма небольшого числа слагаемых, но a_ij (влияние человека на кого-либо) могут быть ненулевыми для огромного количества j, а влияние a_ji (влияния кого-либо на человека) не так велико, чаще ограничивается сотней. Тут и возникает очень большая несимметрия. 

Примеры участников сети

Мы попытались проинтерпретировать в социологических терминах начальные данные модели. К примеру, кто такой «конформист-карьерист»? Это человек, который в конфликте внутренне не участвует, но есть люди, которые сильно на него влияют, к примеру, начальник.

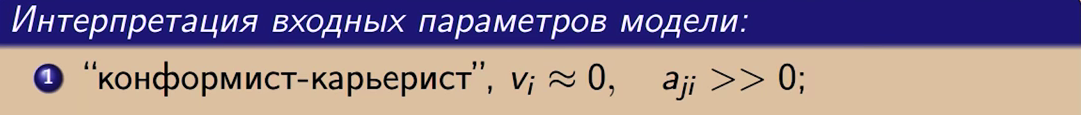
Можно предугадать, как его выбор связан с выбором начальника при любом равновесии.

Далее, «пассионарий» — это человек с сильным внутренним убеждением в стороне конфликта. 

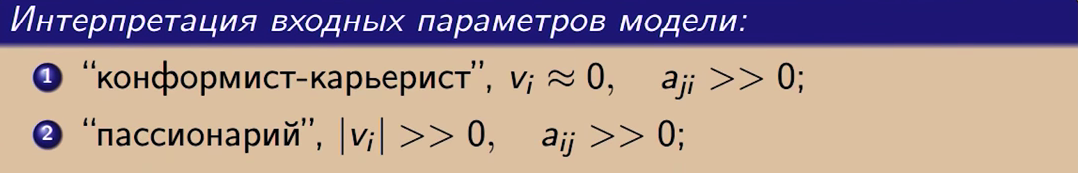
Его a_ij (влияние на кого-либо) велико, в отличии от предыдущего варианта, где велико a_ji (влияния кого-либо на человека).

Далее, «аутист» — человек, который не участвует в игр. Его убеждения около нуля, и влияние на него никто не оказывает.

И, наконец, «фанатик» — это человек, на которого никто вообще не влияет. 

Возможно, с точки зрения лингвистики настоящая терминология неверна, но в этом направлении еще предстоит работа.

Это говорит о том, что у него как и у «пассионария», vi сильно больше нуля, а вот aji = 0. Обращаю внимание, «пассионарий» может быть одновременно «фанатиком». 

Мы предполагаем, что внутри таких узлов будет важно, какое решение принимает «пассионарий/фанатик», т. к. это решение облаком будет распространяться вокруг. Но это не знание, а лишь предположение. Пока мы не можем решить эту задачу ни в каком приближении.

А еще есть сетевизор. Что такое телевизор? Это сдвиг Вашего внутреннего состояния, своего рода «магнитное поле».

При этом влияние телевизора, в отличие от физического «магнитного поля» на все «социальные молекулы» может быть различным как по величине, так и по знаку. 

Можно заменить телевизор на интернет?

Скорее Интернет — это сама модель взаимодействия, надо обсуждать. Назовем это внешний источник, если не информации, то какого-то шума. 

Распишем три возможные стратегии по σ_i=0, σ_i=1, σ_i=-1:

Как происходите взаимодействие. В начале все участники — это «облака», и каждый человек про всех остальных знает лишь то, что это — «облако», и предполагает априорное распределение вероятностей этих «облаков».  Как только конкретный человек начинает взаимодействовать, он узнаёт про себя всю тройку ε, т.е. конкретную точку, и в данный момент человек принимает решение, которое дает ему большее число (из тех, где к выигрышу прибавляется ε, он выбирает то, которое больше двух других), остальные не знают, в какой точке он находится, потому предугадать не могут. 

Далее человек выбирает (σ_i=0/ σ_i=1/ σ_i=-1), и чтобы выбрать, ему необходимо знать σ_j для всех остальных. Обратим внимание на скобку, в скобке есть выражение [∑ _{j ≠ i} a_ji σ_j], т.е. то, что человек не знает. Он должен это предугадывать в равновесии, но в равновесии он не воспринимает σ_j​ как числа, он воспринимает их как вероятности. 

В это есть суть различия равновесия дискретного отклика от равновесия Нэша. Человек должен вероятности предугадать, таким образом возникает система уравнений на вероятности. Допустим, представим систему уравнений на 100 млн человек, умножаем еще на 2. т. к. существуют вероятность выбора «+», вероятность выбора «-» (вероятность остаться в стороне не принимает в расчет, т. к. это зависимый параметр). В итоге 200 млн переменных. И 200 млн уравнений. Решать такое нереально. И собрать такую информацию в точности тоже невозможно. 

Но социологи говорят нам: «Подождите, друзья, мы вам скажем, как надо типологизировать общество». Они спрашивают, задачу на сколько типов мы можем решить. Я говорю, 50 уравнений мы еще решим, компьютер умеет решать систему, где 50 уравнений, даже 100 еще ничего. Они говорят, что это без проблем. А потом пропали, гады. 

У нас действительно была намечена встреча с психологами социологами из Вышки, они сказали, что мы можем написать прорывной революционный проект, наша модель, их данные. И не пришли. 

Если вы хотите спросить меня, почему все так через задницу происходит, я вам говорю, потому что психологи и социологи не приходят на наши встречи. Собрались бы вместе, горы бы свернули.

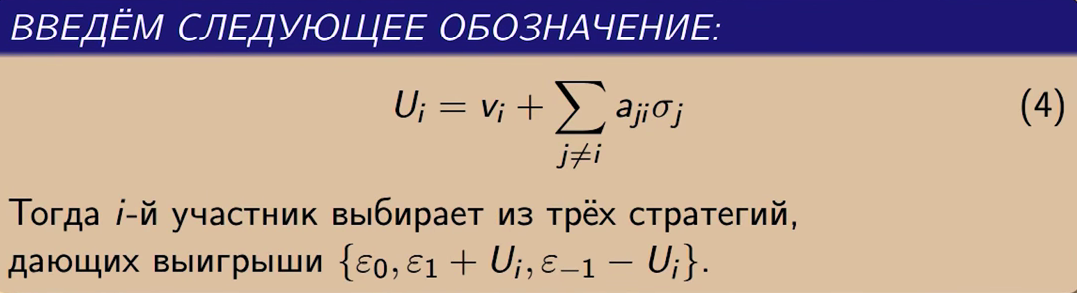
В результате человек должен выбрать из трех возможных стратегий, но не может, т. к. σj он не знает. Тогда меняем σ_j на вероятности.

Выигрыши в равновесии дискретного отклика

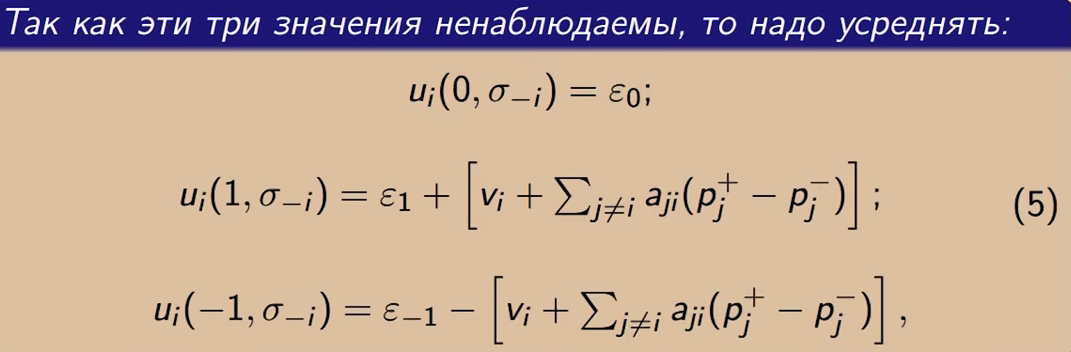
Вместе неизвестного σ_j мы подставляем разницу вероятностей того, что какой-то человек занимает ту или иную из сторон в конфликте. Когда мы знаем, при каком векторе ε в какую точку трехмерного пространства мы попадаем. В этих точках (выигрышах) возникают «облака», и мы можем их проинтегрировать и найти вес каждого из 3 «облаков».

В итоге мы находим вероятности со стороны внешнего наблюдателя, что конкретный человек выберет то или иное, до того, как узнает свое истинное положение. Т. е. это будет формула, которая даст в ответ на знание всех остальных p, свои собственные. И такую формулу можно записать для каждого i и оставить из нее систему уравнений, которая будет знакома тем, кто занимался моделями Изинга и Поца. Статфизика жестко стоит на том, что a_ij = a_ji, взаимодействие не может быть несимметричным.

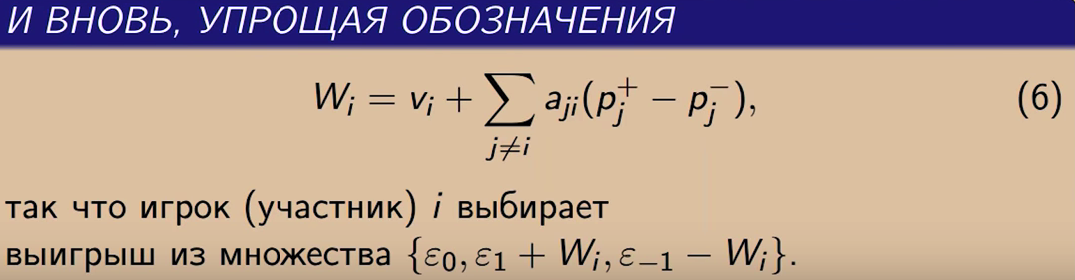
Но здесь есть некоторые «чудеса». Математические «чудеса» а том, что формулы почти совпадают с формулами из соответствующих статфизических моделей, при том, что там нет никакого игрового взаимодействия, а есть функционал, который оптимизируется на множестве всевозможных полей.

При произвольных исходных данных модель ведет себя так, словно в ней кто-то что-то оптимизирует. Такие модели называются «потенциальные игры», в случае, если речь идет о равновесии Нэша. Когда игра устроена так, что равновесия Нэша задаются оптимизацией какого-то функционала на пространстве всех выборов. Что такое потенциальность в равновесии дискретного отклика еще окончательно не сформулировано. (Хотя Федор Сандомирский, возможно, сможет ответить на этот вопрос. Это однозначно стало бы прорывом). 

Вот так выглядит полная система уравнений:

Вероятности, с которыми Вы выбираете то или иное согласованы с прогнозом на Вас. Идея та же, что в равновесии Нэша, но реализована она через вероятности. 

Специальное распределение ε, а именно распределение Гумбеля, которое является неподвижной точкой взятия максимума большого числа независимых случайных величин. 

Нормальное распределение получается, если усреднять большое количество независимых случайных величин с дисперсией в допустимых значениях. А если брать максимум из большого количества независимых случайных величин, то получается такое специальное распределение. 
Кстати, в уравнении пропущен параметр хаотичности принимаемых решений λ, забыл ее написать.

Понимание того, как решать данное уравнение поможет понять, как кластеризовать общество. В теоретическом же аспекте, потенциальность игр с точки зрения уравнения дискретного отклика. 

Надо попробовать реальный социальный граф, который отличается набором свойств: 

• малый диаметр;
• степенной закон распределения степеней вершин;
• высокая кластеризация. 

Т. е. свойства настоящей социальной сети можно попробовать переписать внутрь этой модели. Пока никто не пробовал, возможно тогда что-то получится.

Теперь я могу попробовать ответить на Ваши вопросы. По крайней мере, я точно могу их выслушать.

Как это объясняет механизм Брексита и выборы в США?

Значит так. Это не объясняет ничего. Но это дает намек, почему социологические опросы стабильно ошибаются в прогнозах. Потому что люди публично отвечают то, что требует отвечать их социальное окружение, а наедине с собой отдают свой голос за внутреннее убеждение. И если мы сможем решить это уравнение, что в решении будет то, что нам дал социологический опрос, а v_i— это то, что будет на голосовании.

А этой модели можно отдельным фактором считать не человека, а социальную страту?

Именно это и хотелось бы сделать. Но мы не знаем устройство социальных страт. Именно для этого мы пытаемся угнаться за социологами и психологами.

Вашу модель как-то можно применить для объяснения механизма разного рода социальных кризисов, которые наблюдаются в России? Допустим расхождение между действием формальных институтов?

Нет, это не про то. Это именно про конфликт людей. Я не думаю, что кризис институтов здесь можно как-то объяснить. На эту тему у меня есть твоя собственная идея о том, что институты, созданные человечеством слишком сложны, они не смогут в такой степени сложности держаться и вынуждены будут деградировать. Это мое понимание реальности.

А можно ли исследовать как-то явление поляризации общества? У вас в это v уже заложено, как кому хорошо…

Не совсем, у нас есть там телевизор, v+h. Это сравнительная статика.

Да, но поляризация происходит постепенно. Я имею в виду, что участие общества с ярко выраженной позицией 10% v-положительное, 6% v-отрицательное, и разрыв все больше увеличивается между этими значениями.

Я не знаю, что будет в динамике вообще. В правильно динамике, видимо, v будут принимать значения предыдущих σ. Но получится ли такой эффект, я не знаю. Панацеи не существует, нет универсальной модели общества. Эта модель — некоторый взгляд, который может быть полезен. Я верю, что если мы решим эту задачу, то увидим, как соцопросы стабильно расходятся реальностью голосования. В социуме огромный хаос. Даже измерения определенного параметра дает разные результаты. 

Это как-то связано с классической теорией матричных игр?

Это и есть матричные игры. Просто матрицы тут размером 200 млн на 200 млн. Это игра всех со всеми, матрица записана в виде функции. С матричными играми это связано так: матричные игры — это игры двух людей, а здесь играют 200 млн. Потому это тензор, который имеет размерность 200 млн. Даже не матрица, а куб, размерностью 200 млн. Но в них рассматривается необычная концепция решения.

А есть ли понятие цены игры?

Цена игры возможна только в антагонистической игре двух игроков, т.е. с нулевой суммой. Это неантагонистическая игра огромного числа игроков. Вместо цены игры есть равновесные выигрыши, причем не в равновесии Нэша, а в равновесии дискретного отклика.

А понятие «стратегии»?

Стратегии есть, 0, -1, 1. Это вышло из классической концепции равновесия Нэша-Байеса, равновесие игр с неполной информацией. И в конкретном случае, равновесие Байеса-Нэша положено на данные обычной игры. За счет этого и получается комбинация, называемая равновесие дискретного отклика. И это бесконечно далеко от матричных игр середины XX века.

Что-то сомнительно, что с миллионом игроков вы что-то сможете сделать...

В этом и вопрос, как кластеризовать общество, решить игру с таким количеством игроков невозможно, Вы правы.

Литература по близким направлениям в статфизике и социологии

1. Dorogovtsev S. N., Goltsev A. V., and Mendes J. F. F. Critical phenomena in complex networks // Reviews of Modern Physics. 2008. Vol. 80. Pp. 1275—1335.
2. Lawrence E. Blume, Steven Durlauf Equilibrium Concepts for Social Interaction Models // International Game Theory Review. 2003. Vol. 5, (3). Pp. 193—209.
3. Gordon M. B. et. al., Discrete Choices under Social Influence: generic Perspectives // Mathematical Models and methods in Applied Science. 2009. Vol. 19. Pp. 1441—1381.
4. Bouchaud J.-P. Crises and Collective Socio-Economic Phenomena: Simple Models and Challenges // Journal of Static Physics. 2013. Vol. 51(3). Pp. 567—606.
5. Sornette D. Physics and financial economics (1776—2014): puzzles, lsing, and agent-based models // Reports on Progress in Physics. 2014. Vol. 77, (6). Pp. 1-287

 

Автор: Asya_Dyu

Источник