Первая часть
Первая часть второй части
Вторая часть второй части
Ну что ж, господа, пора заканчивать. В последней статье цикла (название которой разрывает мой ещё толком не проснувшийся шаблон) мы поставим жирную точку в истории этой задачи. Несмотря на то, что в комментариях ко второй части был предложен более удобный и универсальный способ это сделать, я всё же воспользуюсь инструментарием, разработанным лично мной ещё до написания первой из статей. Во-первых, не пропадать же добру, а во-вторых, я думаю, все понимают, что задача — это просто повод порисовать красивые чертёжики в GeoGebra и запостить их на хабр. Ну, как говорится, понеслась.
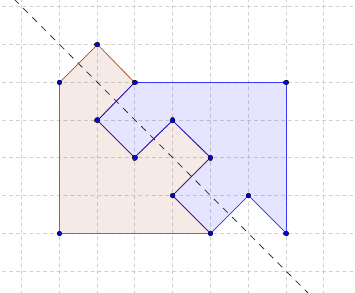
Случай 3: скользящая симмметрия
Скользящая симметрия определяется следующими параметрами: осью симметрии и параллельным ей вектором сдвига. Ось симметрии, в свою очередь, определяется направлением и конкретным положением на плоскости. Сейчас я набросаю некоторое количество следующих друг из друга фактов, достаточно очевидных, чтобы не называть их даже леммами, и уж тем более не доказывать.
- Ось скользящей симметрии равноудалена от границ (понятие границы невозбранно берём из случая параллельного переноса).
- Если взять отрезок с концами на разных границах, то ось симметрии пройдёт через его середину.
- Задав направление оси скользящей симметрии, мы автоматически узнаём и её конкретное положение. Если обе границы состоят из единственной точки, то мы знаем ещё и вектор сдвига.
- Части, на которые фигура делится осью, имеют равную площадь (этот факт не следует из предыдущих)
Вооружившись этими фактами, я нарисовал вот такую картинку:
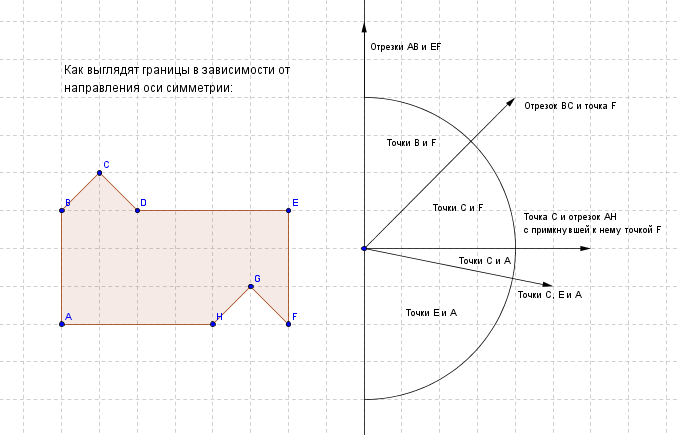
Из неё видно, что для большинства направлений на границах окажутся либо точки А и Е, либо точки B и F, а следовательно, ось пройдёт через «центр» фигуры (пересечение диагоналей прямоугольника ABEF). Второе место по распространённости занимает случай с точками C и F, почётное третье — с точками C и A. В этих случаях, очевидно, ось симметрии будет проходить через середины отрезков CF и CA соответственно.
Теперь посмотрим, при каких направлениях ось будет делить фигуру на две равновеликих части. Не вдаваясь в утомительные подробности, скажу просто: а вот в таких.

Теперь у нас есть три конкретных оси и, более того, к ним прилагаются три конкретных вектора сдвига — ведь границы во всех случаях состоят из одной точки. Нетрудно показать, что для всех этих трёх скользящих симметрий найдутся точки фигуры, для которых нет ни образа, ни прообраза — что, согласно лемме 3, означает, что это плохие, негодные скользящие симметрии, которые не могут соответствовать разбиению фигуры на две равные части. Поиск конкретных точек я оставляю читателю.
Вывод
Фигуру А0 нельзя разрезать на две равные части. Теперь я с чистой совестью пойду пересматривать «А зори здесь тихие». С Днём Победы, товарищие.
Автор: Sirion






