Серьёзный прорыв в деле решения гипотезы 60-летней давности проливает свет на то, как при росте случайных систем в них начинает появляться порядок

Команда из математиков и специалистов по информатике, наконец, продемонстрировала прогресс в решении, на первый взгляд, простой задачи, терзавшей исследователей почти шесть десятилетий.
Эта задача, поставленная математиками Палом Эрдёшем и Ричардом Радо в 1960-м, касается того, как часто можно ожидать появления узоров, напоминающих подсолнух, в больших наборах объектах – например, в большом количестве точек, рассыпанном на плоскости. И хотя новый результат не решает гипотезу Эрдёша и Радо полностью, он продвигает понимание математиков в вопросе появления удивительно сложных структур в случайных скоплениях. Для этого в работе задачу переформулировали в терминах компьютерной функции, воспользовавшись преимуществами становящейся всё более тесной взаимосвязи между теоретической информатикой и чистой математикой.
«В этой работе по-новому проявляется математическая идея, которая станет главнейшей идеей нашего времени. Сам по себе результат работы потрясающий», — сказал Гил Калай из Еврейского университета в Иерусалиме.
Гипотеза о подсолнухе относится к множествам, или к наборам объектов. Проще всего её представить на примере множества точек на плоскости xy. Сначала выберите фиксированное количество точек, которое войдёт в каждое множество. Затем нарисуйте случайные петли так, чтобы каждая петля, или множество, включала в себя выбранное количество точек. Петли могут пересекаться, и некоторые точки могут попасть в несколько множеств, напоминая диаграмму Венна.
Если нарисовать достаточно много петель, содержащих большое количество точек, большая часть из них будет пересекаться и будет напоминать хитросплетение лиан. Но Эрдёш и Радо предсказали, что также в результате появится утончённая структура: три или более множества будут пересекаться друг с другом, оставляя на пересечении одно и то же подмножество точек, при этом ни одно из этих множеств не будет пересекаться ни с какими другими множествами.
Если удалить это общее подмножество точек, тогда три множества окажутся расположенными вокруг пустоты, и будут полностью отделены друг от друга – как лепестки вокруг тёмной середины подсолнуха. Простейшим подсолнухом считается имеющий три множества, не пересекающиеся ни с какими другими; такие острова называются дизъюнктными множествами.
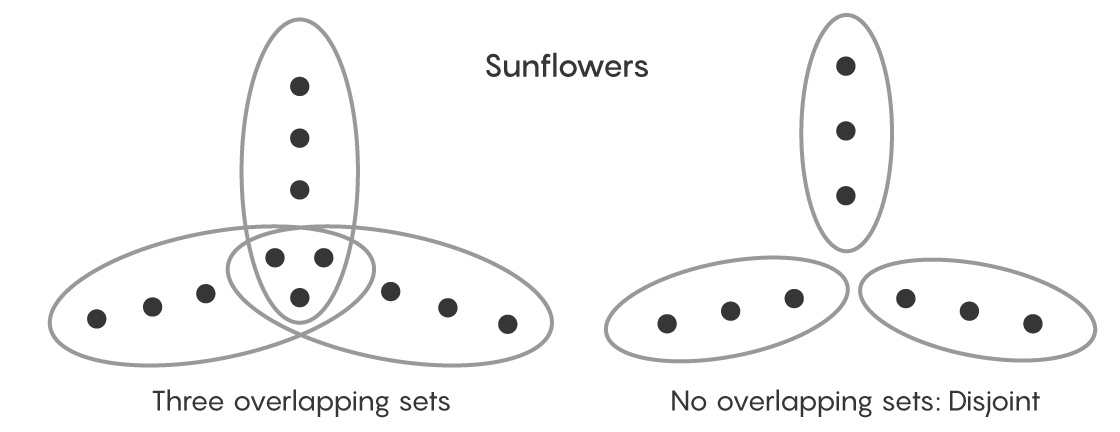
Эрдёш и Радо предположили, что с увеличением количества петель неизбежно будут появляться такие подсолнухи, либо в виде дизъюнктных множеств, либо в виде множеств, накладывающихся друг на друга указанным образом. Эта гипотеза о подсолнухе является частью более общей области математики под названием теория Рамсея, изучающая то, как с увеличением размера случайных систем в них начинает появляться порядок.
«Если у вас есть некий достаточно большой математический объект, в нём должна прятаться некая структура», — сказал Шачар Ловет из Калифорнийского университета в Сан-Диего, соавтор новой работы, над которой также работали Райан Альвейс из Принстонского университета, Кевен Ву из Пекинского университета и Цзяпэн Чжан из Гарвардского университета.
Эрдёш и Радо хотели узнать, сколько именно множеств и какого именно размера нужно, чтобы гарантированно получить подсолнух. Они сделали первый скромный шаг к решению задачи, определив параметр w, обозначающий количество точек в каждом из множеств. Затем они доказали, что требуется порядка ww множеств размера w, чтобы в них гарантированно появился подсолнух, состоящий из трёх множеств. Так что, если вы хотите использовать множества из 100 точек, то вам потребуется 100100 множеств для гарантированного появления подсолнуха.
В то же время Эрдёш и Радо предположили, что на самом деле количество множеств, гарантирующее подсолнух, гораздо меньше, чем ww — и больше похоже на константу в степени w (допустим, 3w или 80w или 5 000 000w). Однако они не смогли найти способа доказать свою догадку.
«Они сказали, что задача кажется чрезвычайно простой, и удивлялись, что не могут достичь в ней прогресса», — сказал Альвейс.
И они были не одиноки. В период от их первого результата и этой новой работы, появившейся спустя 60 лет, только двое математиков достигли хоть какого-то прогресса в этом вопросе – и то они шли постепенно, сделав один шаг в 1997 году, а второй в этом году.
«Все уже испробовали все идеи, с которыми люди чувствовали себя комфортно», — сказал Ануп Рао из Вашингтонского университета, опубликовавший дополнительную работу, упрощающую методы, полученные в новом результате. «И никто не смог улучшить базовую границу, установленную Эрдёшем и Радо».
Но в новом доказательстве сделан серьёзный прорыв.
Четыре исследователя, среди которых есть и математики, и специалисты по информатике, смогли сделать это, разбив задачу на два разных сценария. В первом, более лёгком, они смотрели, что произойдёт, когда множества значительно пересекаются друг с другом, благодаря чему значительно легче понять, когда там должен появиться подсолнух.
«Когда у вас есть набор элементов, принадлежащих к более крупному набору множеств, эту структуру можно использовать» для поиска подсолнуха, сказал Ловет.
Сначала исследователи задались вопросом, существует ли множество точек, принадлежащее достаточно большой части всех множеств в системе. Найдя такие точки, в своих поисках подсолнуха они ограничились только той частью множеств, которые содержат это множество точек. Дальше они продолжили действовать так же, уточняя поиск, включая в него всё меньшее и меньшее количество множеств системы, у которых есть всё больше и больше общих точек. Такая подрезка продолжалась, пока они не нашли свой подсолнух.
Во втором, более сложном сценарии, они анализируют, что произойдёт, если множества не будут сильно пересекаться. В таком случае наиболее вероятным способом получить подсолнух будет взять три дизъюнктных множества. Однако доказать, что три отдельных множества прячутся в большем количестве слегка пересекающихся множеств, нелегко.
Тут и вступает в дело информатика. Двое соавторов, Ловет и Чжан, уже несколько лет пытались анализировать задачу о подсолнухе при помощи тех же инструментов, которые специалисты по информатике используют для изучения булевых функций. Эти функции выполняют операции на последовательности битов – единиц и нулей – и выдают единственный бит в итоге, соответствующий тому, истинно или ложно вычислительное утверждение. К примеру, булеву функцию можно запрограммировать выдавать 1, если хотя бы один из входящих битов равен 1, и 0, если ни один из входящих битов не равен 1.
Три года назад Ловет и Чжан поняли, что таким же образом можно поставить и вопрос о том, есть ли среди набора не сильно пересекающихся множеств три дизъюнктных. Во-первых, назначаем каждой точке в множестве метку: 1, если она содержится только в этом множестве, и 0 в другом случае. Булева функция выдаёт 1 (истина), если каждая точка на входе равна 1 – то есть, каждая точка множества существует исключительно в этом множестве, что делает это множество дизъюнктным. Истинный результат говорит о том, что для нахождения подсолнуха существуют подходящие условия.
Строго доказывая это соответствие, исследователи задействовали обширные знания, касающиеся булевых функций, для атаки на задачу о подсолнухе, на которую раньше не хватало ресурсов. Они доказали, что для получения подсолнуха достаточно будет (log w)w множеств. Такого результата недостаточно для доказательства гипотезы о том, что некоей константы в степени w хватит для получения подсолнуха. Но это на порядок лучший результат, чем ww, полученный Эрдёшем и Радо, и он примерно совпадает с тем количеством множеств, которое они предсказывали.
После полувека неудач новая работа позволяет предположить, что мы скоро увидим и полное решение. Она также улучшает понимание того, как особые формы с неизбежностью возникают в дикой математической природе случайностей.
Автор: Вячеслав Голованов






