Древние греки интересовались, можно ли приблизительно выразить иррациональные числа дробями. Доказав давнюю гипотезу Даффина-Шаффера, два математика дали исчерпывающий ответ.
Двоичная запись π бесконечна. Но бесконечное число дробей могут приближаться к этому числу со всё возрастающей точностью.
Глубокие провалы на числовой прямой не так неприступны, как могло показаться. Это одно из последствий нового значимого доказательства того, как сложные числа поддаются простым приближениям.
Доказательство разрешает задачу почти 80-летней давности, известную, как гипотеза Даффина-Шаффера. Тем самым оно даёт окончательный ответ, занимавший математиков с древних времён: при каких условиях возможно представлять иррациональные числа, длящиеся бесконечно долго – типа числа пи – простыми дробями типа 22/7? Доказательство устанавливает, что ответ на этот довольно общий вопрос обнаруживается в результате единственного вычисления.
«Существует простой критерий того, можно ли аппроксимировать практически любое число или практически ни одного числа», — сказал Джеймс Мэйнард из Оксфордского университета, соавтор доказательства, сделанного им совместно с Димитрисом Кукулопулосом из Монреальского университета.
Математики несколько десятилетий подозревали, это этот простой критерий является ключом к пониманию того, когда можно получить хорошую аппроксимацию – но не могли доказать этого. Кукулопулос и Мэйнард смогли сделать это только после того, как они переформулировали эту задачу о числах в терминах связей между точками и линиями графа – кардинальное изменение перспективы.
«Я бы сказал, они были достаточно уверенными в себе (и это, очевидно, было оправдано), чтобы пойти по избранному пути, — сказал Джеффри Ваалер из Техасского университета в Остине, приложившего руку к ранним результатам, связанным с гипотезой Даффина-Шаффера. – Прекрасная работа».
Арифметический эфир
С рациональными числами всё просто. В них входят числа для счёта предметов и все остальные числа, которые можно записать в виде дробей.
Благодаря этой способности быть записанными, рациональные числа знакомы нам лучше всего. Однако среди всех вещественных чисел рациональных на самом деле довольно мало. Большая часть чисел – иррациональные, с бесконечной десятичной записью, и их невозможно записать в виде дробей. Некоторые из них оказались достаточно важными для того, чтобы заслужить символические обозначения – пи, е, √2. Остальные нельзя даже назвать. Они повсюду, но недостижимы – словно арифметический эфир.
Возможно, поэтому, естественно будет задуматься – если мы не можем точно выразить иррациональные числа, как близко мы можем подойти к ним? Это область рационального приближения. Математики древности поняли, что неуловимое отношение длины окружности к диаметру можно неплохо приблизить при помощи дроби 22/7. Позднее математики обнаружили ещё более точное и почти такое же сжатое приближение к пи: 355/113.
«Записать пи очень сложно, — сказал Бен Грин из Оксфорда. – Люди пытались найти наиболее точное приближение к пи, и одним из распространённых способов сделать это было использование рациональных чисел».

В 1837 году математик Петер Густав Лежён Дирихле обнаружил правило, говорящее нам, насколько точно можно аппроксимировать иррациональные числа при помощи рациональных. Приближение легко найти, если не устанавливать точного значения ошибки. Но Дирихле доказал наличие чёткой взаимосвязи между дробями, иррациональными числами и разделяющими их ошибками.
Он доказал, что для любого иррационального числа существует бесконечно много дробей, приближающихся к нему всё ближе и ближе. Точнее, ошибка каждой дроби будет не больше, чем 1, делённая на квадрат знаменателя. К примеру, дробь 22/7 приблизительно выражает пи с точностью в 1/72, или 1/49. Дробь 355/113 отстоит от пи не дальше, чем на 1/1132, или 1/12 769. Дирихле доказал, что существует бесконечно много дробей, всё ближе и ближе подбирающихся к пи с увеличением знаменателя.
«Удивительная и примечательная вещь – возможность приближённо выразить вещественное число через дробь, с ошибкой, не превышающей единицы, делённой на квадрат знаменателя», — сказал Эндрю Грэнвиль из Монреальского университета.
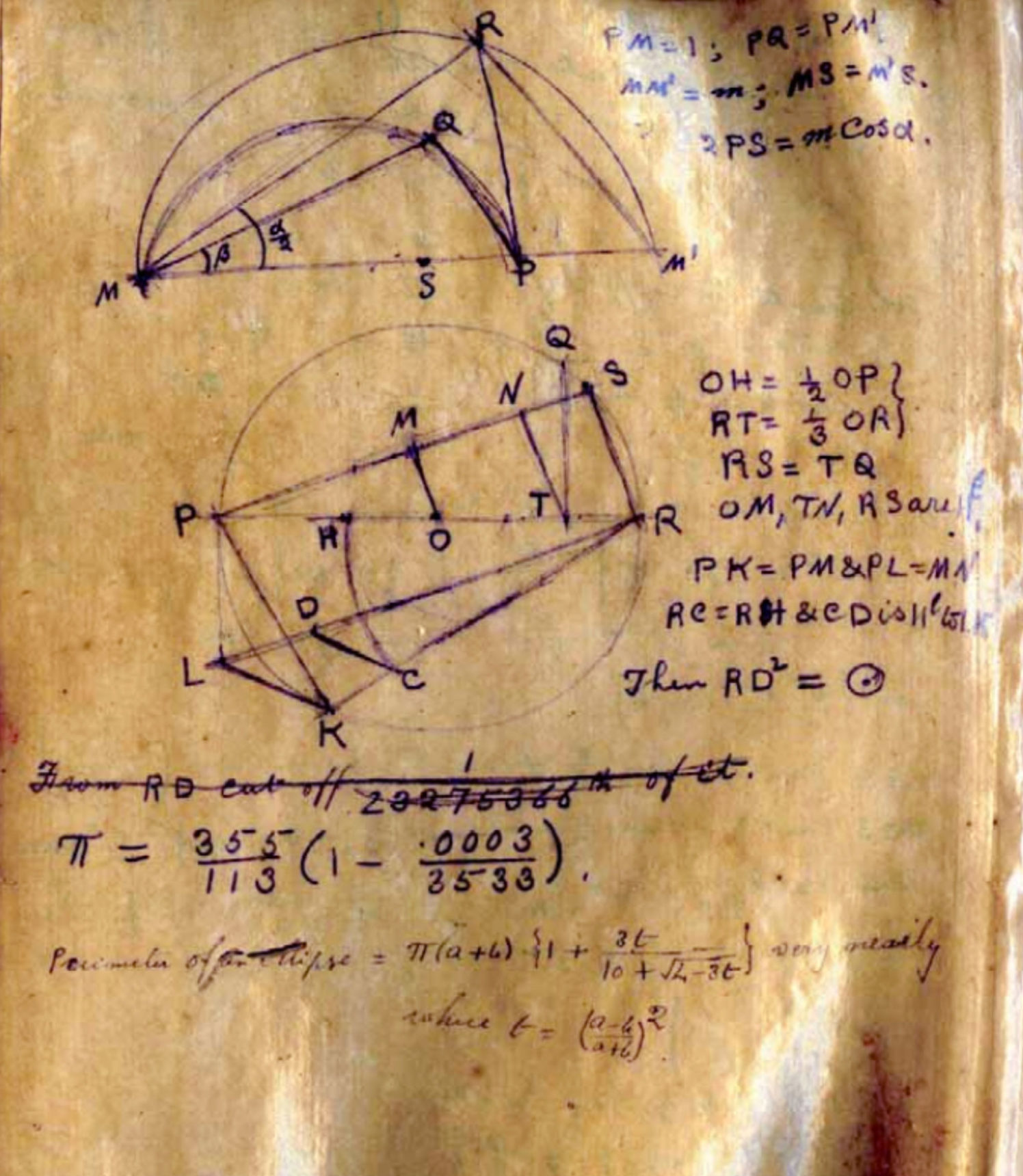
В рукописи 1913 года математик Сриниваса Рамануджан Айенгор использовал дробь 355/113 в качестве рациональной аппроксимации пи.
Открытие Дирихле было ограниченным заявлением по поводу рационального приближения. Оно говорит, что для любого иррационального числа вы можете найти бесконечно много приближающихся к нему дробей, если вы можете использовать в качестве знаменателя любое целое число, и вас устраивает ошибка в размере его обратного квадрата. Но что, если вам нужно, чтобы знаменатели принадлежали к некоторому (бесконечному) подмножеству целых чисел, к примеру, к множеству простых чисел, или к множеству полных квадратов? Что, если вам нужно, чтобы ошибка приближения равнялась 0,00001, или имела любое другое значение? Удастся ли вам найти бесконечно много аппроксимирующих дробей именно в таких условиях?
Гипотеза Даффина-Шаффера – попытка создать наиболее обобщённую платформу для работы с рациональными аппроксимациями. В 1941 году математики Р. Д. Даффин и А.С. Шафер представили следующий сценарий. Сначала выберем бесконечный список знаменателей. Это может быть всё, что хотите: нечётные числа, числа, делящиеся на 10, простые числа.
Потом для каждого числа в списке выберите, насколько точно вам нужно приблизить иррациональное число. Интуиция говорит нам, что если мы выберем достаточно большие ошибки, у нас будет больше возможности для аппроксимации. Если выбрать небольшой размер ошибки, это будет сложнее. «Подойдёт любая последовательность, если оставлять достаточно места», — сказал Кукулопулос.
Теперь, учитывая выбранные параметры – последовательность чисел и определённую ошибку – возникает вопрос: можно ли найти бесконечно много дробей, приближающих все иррациональные числа?
Гипотеза обеспечивает математическую функцию для оценки этого вопроса. Ваши параметры выступают в качестве входных данных. Результатом может быть один из двух вариантов. Даффин и Шаффер предположили, что два этих варианта соответствуют как раз тому, сможет ли ваша последовательность аппроксимировать практически все иррациональные числа с требуемой точностью, или практически ни одно из них («практически» упоминается потому, что для любого набора знаменателей всегда будет существовать небольшое число изолированных иррациональных чисел, которые можно или нельзя достаточно хорошо приблизить).
«Вы получаете практически всё или практически ничего. Промежуточных вариантов нет», — сказал Мэйнард.
Это было чрезвычайно общее заявление, пытающееся характеризовать аппроксимацию рациональными числами вдоль и поперёк. Критерий, предложенный Даффином и Шаффером, казался математикам правильным. Однако доказать, что в двоичном выходе функции содержится всё, что нужно для того, чтобы понять, работает ваша аппроксимация, или нет – вот это было сделать гораздо сложнее.
Двойной подсчёт
Доказательство гипотезы Даффина-Шаффера связано с тем, чтобы понять, какую пользу вы получаете с каждого из доступных вам знаменателей. Чтобы ощутить это, полезно будет рассмотреть уменьшенную версию этой задачи.
Допустим, вы хотите аппроксимировать все иррациональные числа на отрезке от 0 до 1. Представим, что в качестве знаменателей вам доступны все натуральные числа от 1 до 10. Список возможных дробей достаточно большой. Сначала 1/1, затем 1/2 и 2/2, потом 1/3, 2/3 и 3/3, и так далее, вплоть до 9/10 и 10/10. Однако пользы от них никакой.
К примеру 2/10 – то же самое, что 1/5, а 5/10 – то же самое, что 1/2, 2/4, 3/6 и 4/8. До появления гипотезы Даффина-Шаффера советский математик Александр Яковлевич Хинчин сформулировал похожую по широте гипотезу о рациональной аппроксимации. Однако его теорема не учитывала тот факт, что эквивалентные дроби нужно считать только по одному разу.

Димитрис Кукулопулос (слева) и Джеймс Мэйнард на презентации своего доказательства на конференции в Италии
«Обычно математика для первого класса не должна влиять на решение задач, — сказал Грэнвиль. – Но в данном случае, как ни удивительно, она повлияла».
Поэтому в гипотезе Даффина-Шаффера есть член, подсчитывающий количество уникальных дробей (или приведённых дробей) для каждого знаменателя. Этот член называется функцией φ Эйлера в честь её изобретателя, математика XVIII века Леонарда Эйлера. φ(10) равняется 4, поскольку между 0 и 1 существует всего четыре приведённых дроби со знаменателем 10: 1/10, 3/10, 7/10 и 9/10.
Следующий шаг – посчитать, сколько иррациональных чисел можно аппроксимировать при помощи каждой из приведённых дробей. Это зависит от того, ошибку какого размера вы готовы принять. Гипотеза Даффина-Шаффера позволяет выбирать ошибку для каждого из знаменателей. Например, для дробей со знаменателем 7 можно взять допустимую ошибку 0,02. Для знаменателя 10 можно взять ошибку 0,01.
Определив знаменатели и члены ошибок, пора ставить сети на иррациональные числа. Постройте ваши дроби на числовой прямой между 0 и 1, а ошибки нарисуйте в виде сетей, отходящих от дроби с каждой стороны. Можно сказать, что все иррациональные числа, попавшие в сети, «удовлетворительно аппроксимированы» для заданных членов. Вопрос в следующем: сколько иррациональных чисел вы поймали?
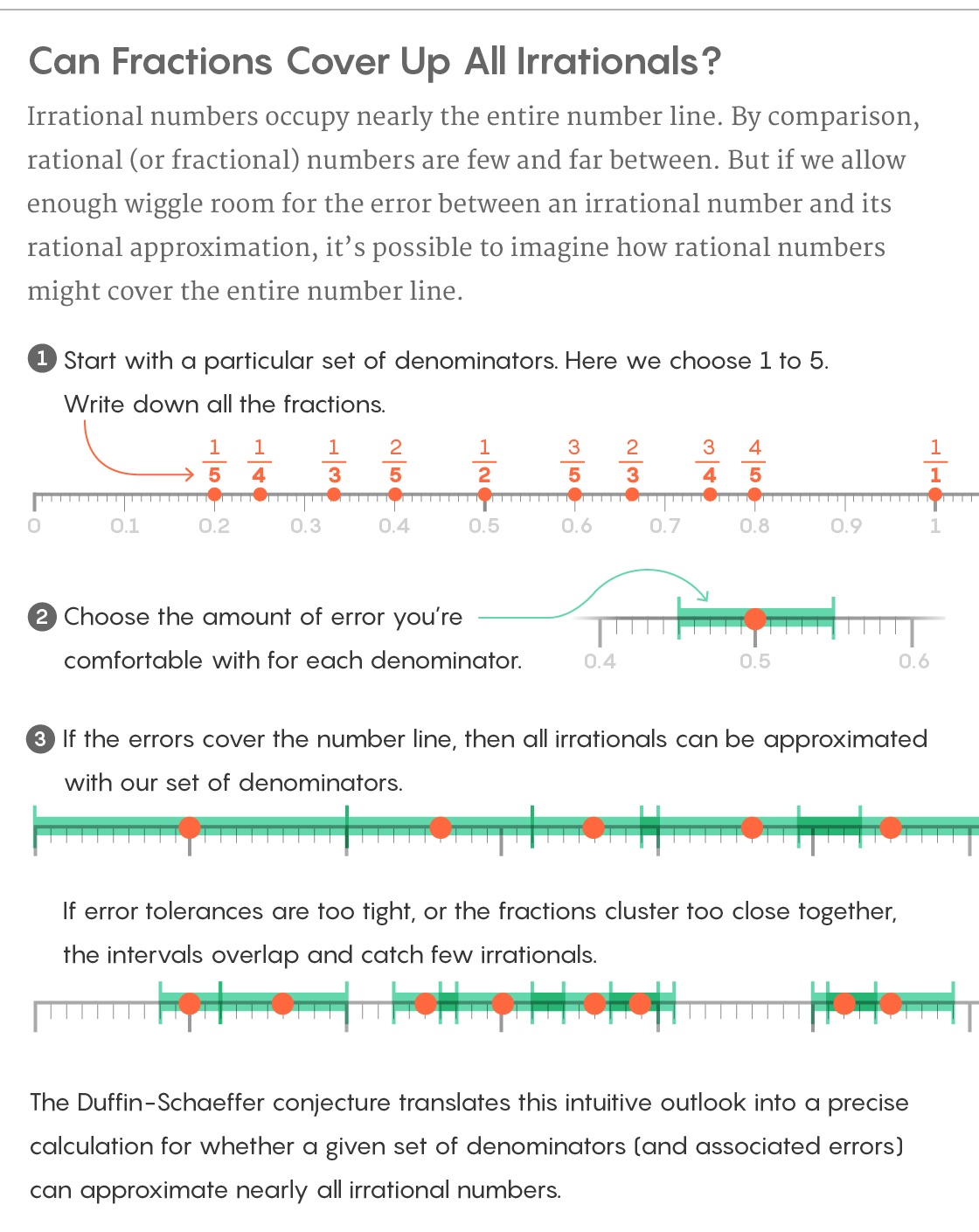
В любом интервале числовой прямой содержится бесконечное количество иррациональных чисел, поэтому точное количество пойманных иррациональных чисел написать нельзя. Вместо этого математики говорят о пропорции общего количества иррациональных чисел, пойманных каждой дробью. Они оценивают эти пропорции при помощи такой концепции, как «мера» подмножества чисел – это что-то вроде оценки количества пойманной рыбы по весу, а не по количеству.
Гипотеза Даффина-Шаффера предлагает сложить все меры подмножеств иррациональных чисел, пойманных каждой из аппроксимирующих дробей. Она представляет это число в виде большой арифметической суммы. Затем она делает своё главное предсказание: если эта сумма уходит в бесконечность, то вы аппроксимировали практически все иррациональные числа; если же она даёт лишь конечное значение, вне зависимости от того, сколько мер вы просуммировали, тогда вам не удалось аппроксимировать практически ни одного иррационального числа.
Подобный вопрос, «расходится» ли сумма до бесконечности или «сходится» к конечному значению, возникает во многих областях математики. Главное заявление гипотезы Даффина-Шаффера состоит в том, что если вы хотите понять, можете ли вы аппроксимировать почти все иррациональные числа при помощи заданного множества знаменателей и допускаемых ошибок, то вам нужно знать только одно: расходится ли бесконечная сумма мер до бесконечности, или сходится к конечному значению.
«В итоге, неважно, как вы решили оценивать аппроксимацию для каждого знаменателя, ваш успех целиком зависит только от одного: расходится ли бесконечная последовательность, или нет», — сказал Ваалер.
Построение решения
Вы можете задаться вопросом: а что, если числа, аппроксимированные одной дробью, пересекутся с числами, аппроксимированными другой? Не будем ли мы учитывать их по два раза при подсчёте мер?
Для некоторых последовательностей аппроксимации двойной подсчёт не имеет значения. Математики уже несколько десятилетий назад доказали, что эта гипотеза выполняется для последовательностей аппроксимации, состоящих из простых чисел. Но для многих других последовательностей аппроксимации двойной подсчёт представляет проблему. Поэтому математики и не могли разобраться с этой гипотезой в течение 80 лет.
Степень, до которой различные знаменатели отлавливают пересекающиеся множества иррациональных чисел, отражается в количестве простых делителей, общих для всех знаменателей. Рассмотрим числа 12 и 35. Простые делители у 12 – это 2 и 3. Простые делители у 35 – это 5 и 7. Иначе говоря, общих простых делителей у 12 и 35 нет – в итоге, множества иррациональных чисел, которые можно аппроксимировать долями со знаменателями 12 и 35 не особенно пересекаются.
А что насчёт знаменателей 12 и 20? У 20 простые делители – это 2 и 5, пересекающиеся с делителями 12. Точно так же и иррациональные числа, которые можно аппроксимировать дробями со знаменателем 20, пересекаются с теми, которые можно аппроксимировать дробями со знаменателем 12. Гипотезу Даффина-Шаффера тяжелее всего доказать именно в таких ситуациях — когда у чисел в аппроксимационной последовательности есть много общих небольших простых делителей, и происходит пересечение многих подмножеств чисел, которые аппроксимирует каждый из знаменателей.
«Когда у многих знаменателей из которых вы выбираете есть много небольших простых делителей, они начинают мешать друг другу», — сказал Сэм Чау из Оксфорда.
Ключ к решению гипотезы заключался в поиске способа точно подсчитать взаимные наложения подмножеств иррациональных чисел, которые аппроксимируются знаменателями, имеющими общие простые делители. 80 лет этого никому не удавалось сделать. Кукулопулос и Мэйнард добились успеха, найдя совершенно новую точку зрения на задачу.
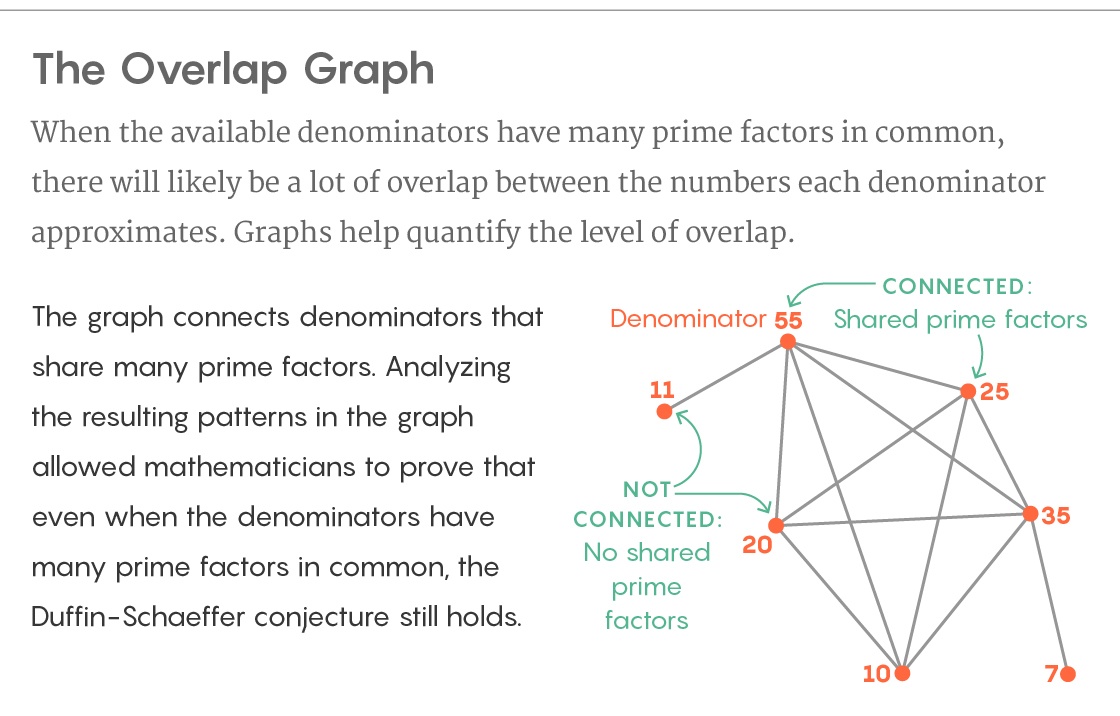
Граф взаимного наложения
В своём новом доказательстве они строят из своих знаменателей граф. Они строят их в качестве вершин графа и соединяют вершины ребром, если у них есть множество общих простых делителей. Структура графа описывает наложение подмножеств иррациональных чисел, которые аппроксимирует каждый из знаменателей. И хотя это наложение тяжело исследовать напрямую, Кукулопулос и Мэйнард нашли способ анализировать структуру графа при помощи инструментов из теории графов – и нужная им информация нашлась таким путём.
«Граф помогает визуально разбираться в задаче, это красивый язык, на котором можно размышлять о проблеме», — сказал Кукулопулос.
Кукулопулос и Мэйнард доказали, что гипотеза Даффина-Шаффера и в самом деле верна: если вам дали список знаменателей с допустимыми ошибками, вы можете определить, возможно ли аппроксимировать практически все иррациональные числа, или это невозможно сделать, просто проверяя, расходится ли соответствующая сумма мер в бесконечность или сходится к конечному значению.
Это элегантная проверка, берущая обширный вопрос природы аппроксимации рациональными числами и сводящая его к единому вычисляемому значению. Доказав универсальность проверки, Кукулопулос и Мэйнард совершили один из величайших поступков для математики: дали окончательный ответ на основополагающий вопрос в своей области.
«Их доказательство стало необходимым и достаточным результатом, — сказал Грин. – Полагаю, он отмечает конец очередной главы в математике».
Автор: Вячеслав Голованов






