В предыдущих сериях мы взглянули на дробные числа с несколько необычных ракурсов. В этой серии, после введения и некоторой теоретической базы, попробуем собрать всё в удобном виде и получить пользу от имеющейся информации.
Поиск простых.
Поговорив о свойствах таблицы остатков, мы можем попробовать применить знания о ней и к зарабатыванию. Так многие в мире считают полезным поиск больших простых чисел. И даже существуют организации, готовые отдать много денег тому, кто найдёт большое простое число. Но так же в мире популярна тема квантовых вычислений. Почему? Потому что она обещает взлом известной криптосистемы. Это, так сказать, рекламный лозунг квантовых вычислений, позволяющий убедить любого принимающего решения менеджера в необходимости выделить денег на такое интересное занятие. Поэтому поговорим и мы на эту тему.
Сначала расскажем, как ищут простые числа. Основная проблема здесь — количество. Для больших чисел просто нет алгоритмов, которые позволяют быстро проверить, простое число перед нами или составное. Поэтому максимальное простое на сегодня — длиной менее 25 миллионов десятичных знаков. Это всего 10 мегабайт, на таких массивах современные процессоры показывают миллисекундные времена обработки, но чтобы проверить, простое ли число находится в нашем массиве, современный процессор будет потреблять электричество и жужжать вентилятором десятки лет. То есть технически размер для процессора плёвый, но вот количество операций в известных алгоритмах для таких больших чисел — просто огромное. Почему сложилась такая ситуация?
Для тестов простоты применяют, например, перебор делителей. Но сколько делителей нужно перебрать для числа, длиной в десять мегабайт? Ответ — даже атомов с электронами во всей вселенной хватит лишь на крохотную часть этой величины. То есть нам нужны огромные количества вселенных, просто что бы разместить там все эти делители. Многовато? Поэтому перебор делителей для десятимегабайтных чисел применяют ограниченно (да, вселенная подкачала...), но к счастью есть другие алгоритмы. Можно выделить алгоритмы, которые не используют перебор делителей, и при этом гарантированно дают ответ — простое перед нами или составное. Но это очень медленные алгоритмы. То есть они, конечно, способны перемалывать числа размером этак бит сто-двести, но десять мегабайт для них — это смерть всему и сразу. Поэтому приходится выкручиваться хитрыми способами.
Но проблема всех хитрецов в том, что не придумали пока полной теории делимости. Ведь была бы она полной, мы бы очень быстро нашли ответ — простое число или нет. Точнее — теория быстро дала бы нам алгоритм для проверки, который не заставлял бы нас ждать до тепловой смерти вселенной. Вот поэтому и дают премии тем, кто придумает алгоритм побыстрее, ну а лучше всего — целую теорию, что бы алгоритмы на все случаи жизни обеспечить.
Пока же в нашем распоряжении есть специфический тест Люка-Лемера, который использует связь так же весьма специфических чисел Мерсенна с некой последовательностью, но не остатков от деления, как мы недавно наблюдали, а сумм степеней некоторых иррациональных чисел. То есть заход на тест простоты выполнен со стороны, скажем так, не совсем очевидной, хотя некоторые здесь могут подобрать более хлёсткие сравнения. Но почему степени иррациональных чисел оказались ближе к тестам простоты, чем все остальные достижения теории чисел? Видимо потому, что математика не знает простых решений. И в результате был использован хоть и не очевидный, но всё же работающий метод из не самой близкой к целочисленным вычислениям области, примерно как переход от декартовых координат к полярным помогает применить дополнительные методы, которые очень сложны при их реализации в декартовых координатах.
Помимо теста Люка-Лемера есть ещё вероятностные тесты. Они помогают отсеять гарантированно составные числа. Так одним из активно используемых вероятностных тестов является тест на основе формулы Ферма, о которой мы недавно говорили. Как он работает? Очень просто — помните столбец из единиц справа в таблице остатков? Это гарантированный признак простоты числа. Для объяснения проверки при помощи формулы Ферма математики используют специфическую терминологию, которую кроме них мало кто понимает, поэтому не будем уходить в эти математические дебри, а объясним всё «на пальцах», точнее — по таблице остатков. Что бы понять, какой остаток будет в последнем столбце, нужно либо произвести деление столбиком и дойти в нём до остатка на позиции, содержащей 1, либо вычислить этот остаток по формуле, которая позволяет получить остаток по номеру позиции и основанию системы счисления. Первый вариант для чисел длиной в десять мегабайт потребует практически бесконечного времени, ведь ширина таблицы равна N-1, а это значит, что уже для числа порядка миллиона в таблице будет минимум миллион столбцов. Для миллиарда — миллиард. Для триллиона — триллион. Но триллион, это всего 12 десятичных знаков. А нас интересует число, в котором под 25 миллионов знаков. Даже триллион остатков по методу деления столбиком нам придётся вычислять вряд ли меньше, чем пол-часа, и это всего 12 десятичных знаков. Всего! В сравнении с 25 миллионами. Как вы думаете, у вас хватит времени дождаться результата таким способом? Вот поэтому лучше вычислить сразу нужное значение, воспользовавшись формулой. И как раз формула Ферма соответствует формуле для вычисления остатка именно в последней позиции в таблице. При этом если период короче ширины таблицы, то математика пока не знает, как его вычислить, а значит нам в любом случае нужно выбирать именно последний столбец. Математики в тесте просто проверяют, а равен ли остаток в последнем столбце для выбранной ими системы счисления единице (хотя математики не оперируют понятием системы счисления, для них есть лишь основание, возводимое в степень). Если остаток не равен единице — число гарантированно составное. Как мы видели на примере таблицы для числа 21 — именно отсутствие единицы в конце многих строк отличает её от таблиц для простых чисел. Но есть одна проблема. В некоторых строках всё же могут оказаться единицы, в чём мы тоже могли убедиться как раз на примере таблицы для 21. Вот поэтому математики и называют тест на основе формулы Ферма вероятностным. То есть они не знают, является ли число простым, если тест Ферма нашёл остаток, равный единице, ведь такие ложные единицы есть и в таблице для числа 21, и во многих других таблицах, даже для десятимегабайтных чисел. Значит нужно либо проверять все строки подряд, что очень долго, ведь строк для десятимегабайтного числа, как было замечено ранее, много больше чем всего сущего в известной нам вселенной, либо просто сказать — вероятно, что это число простое. Вот последний способ и выбрали математики. Благо строк, заканчивающихся на единицу, в большинстве составных чисел немного. Правда есть ещё так называемые числа Кармайкла, у которых все строки, кроме кратных делителям такого числа, заканчиваются на единицу. Так вот на числах Кармайкла вероятностный тест по формуле Ферма ошибается практически гарантированно, ведь для исключения ошибки нужно попасть в строку, кратную делителю числа, а делителей у десятимегабайтного числа может быть всего два, и величина их может быть очень большой, а потому вероятность попасть именно в такую строку при случайном выборе основания системы счисления практически равна нулю. Но с другой стороны — чисел Кармайкла относительно мало, что позволяет надеяться на вероятностный тест. Только при поиске простых чисел надежда на вероятность исключена. Именно поэтому после отбора кандидатов в простые при помощи вероятностных тестов всё же применяется тест Люка-Лемера.
Немного добавим про числа Кармайкла. Они замечательны не только своей способностью имитировать простые. Так, в сети есть сайт, где можно поизучать различные последовательности чисел. Если там ввести в поле для поиска число 561 (минимальное число Кармайкла), то можно обнаружить, что оно участвует в очень большом числе последовательностей. О чём это говорит? Видимо о неких пока неизвестных структурных свойствах подобных чисел, встречающихся в нашем мире очень часто. Весьма занимательный факт.
Но вернёмся к тестам простоты. Не смотря на хороший коэффициент фильтрации вероятностными тестами человечество тратит годы на нахождение очередного максимального простого числа. Почему? Потому что зависимость времени выполнения тестов от размера числа квадратичная. То есть для небольших чисел всё идёт на ура и проблем не возникает, но при возрастании чисел в миллион раз, время на вычисления возрастает в триллион раз. Поэтому на одном ядре процессора мы бы считали тест Люка-Лемера десятки лет. Но даже тест по формуле ферма мы тоже считали бы примерно столько же. То есть у обоих подходов количество вычислений достигло пределов возможностей человечества. С этим надо что-то делать, вы не находите?
Какие могут быть альтернативы столь расточительному растрачиванию вычислительных ресурсов на нагрев воздуха в течении многих лет? Очень просто — нужно предсказать простоту по характеру числа, по его принадлежности к определённому классу. Так числа Мерсенна стали лидерами по достигнутым размерам доказанных простых чисел именно из-за принадлежности к специфическому классу. Тест Люка-Лемера работает именно для такого специфического класса. Числа других классов отстают из-за отстутствия даже такого затратного теста, каким является тест Люка-Лемера для десятимегабайтных чисел (хотя для некотрых всё же этот тест адаптирован). Значит нам нужна классификация чисел, позволяющая находить простые тесты простоты, да простят меня небеса за такой каламбур.
Как создать такую классификацию? Тоже не так сложно — нужно исследовать различные числа и выявить у них общие черты. В общем-то именно этим математики и пытаются заниматься, но пока что не выходит каменный цветок. Поэтому попробуем им помочь.
Описанный ранее подход для анализа чисел на основе таблиц остатков по сути исследует делимость чисел вида 1000...000. То есть к единице постоянно приписываются нолики справа, домножая её тем самым на основание каждой из систем счисления, присутствующих в таблице остатков. В результате анализа мы выяснили, что разные числа делят числа вида 1000...000 по разному. Так простые числа вообще не могут делить единицу с нулями. А вот составные, да ещё, например, из двоек и/или пятёрок — вполне делят. Ниже приведена таблица для числа 8:
Как вы видите, в ней в строках, кратных 2, после некоторого вступления из ненулевых остатков остаются лишь одни нули. Именно так выглядят все числа, относящиеся к классу делителей единицы с нулями, а наличие нулей подсказывает нам, в каких системах счисления нас ждёт успех. Но вот проблема — с точки зрения поиска простых чисел единица с нулями нам совсем не интересна, ведь она гарантированно делится на основание системы счисления, которое и даёт нам все эти нули после единицы. Значит нужно исследовать делимость других классов чисел. Логично? Именно так мы и сделаем.
Может попробуем теорию делимости?
Ранее мы познакомились с закономерностями таблиц остатков для относительно привычной нам операции деления. Закономерности получились занимательные, но у них осталась всё та же проблема — они не дают нам быстрого алгоритма проверки простоты. Для такой проверки нам, как и в тесте по формуле Ферма, придётся возводить числа в очень большую степень, а потом находить остаток от деления результата на исследуемое число. Либо просто перебирать все остатки методом «уголка» (до тепловой смерти вселенной, понятно). Вот данные — операция возведения в степень с нахождением остатка занимает 15 минут на одном ядре для чисел порядка 
. При росте размера числа в 1000 раз получим квадратичный рост (плюс логарифмы, но это уже не так много) в 1000000 раз минимум, а в реальности — во много миллионов раз. Допустим, в результате получим миллион часов на один тест. Это примерно 40000 дней или заметно больше ста лет. Если заоптимизировать выполнение теста по самые уши, выполнять его с учётом всех особенностей архитектуры процессора, то возможно, вместо ста лет получим 10. На 10 ядрах — 1 год. На 1000 ядер — 4 дня. Но это всего лишь вероятностная проверка, ведь есть маскирующиеся под простые составные числа. Значит нужно ещё перепроверять. Но важнее тот факт, что чисел кандидатов — миллионы. После всех возможных фильтраций их тоже останется немало. Поэтому мир до сих пор возится с десятимегабайтными числами.
Но у нас есть инструмент. Таблица остатков работает и для других типов чисел. Например, возьмём числа Мерсенна. В двоичном виде это просто последовательность единиц. Что нам мешает вместо последовательности нулей исследовать последовательность единиц? Да ничего не мешает. И оказывается, что для такой последовательности наш метод вполне работает и в нём сохраняются ряд ранее выявленных закономерностей. Вот результат для числа 7:
Как мы видим, простое число 7 во всех системах счисления (кроме кратных семи) является делителем чисел Мерсенна. То есть почти в каждой строке присутствует ноль, который говорит нам о делимости чисел вида 111...111 (в двоичной системе) на 7. Так, при работе с двоичной системой счисления, мы видим, что число 7 делит все числа Мерсенна, длина которых кратна 3. Этот результат очевиден и без таблицы остатков — число 7 в двоичном виде состоит из трёх единиц (111), поэтому оно будет делить двоичное число из трёх единиц. А если единиц больше, то деление выглядит так:
111111 | 111
------
111 1001
111
111
111
То есть мы просто укладываем семь (в двоичном виде) под делимым числом. И сколько раз семёрка уложится — столько тройных единиц в делимом числе. Если же в нём число единиц не кратно трём, то такое число не делится нацело на 7. Но это всё очевидно лишь до тех пор, пока мы исследуем числа с идентичной структурой (7 и 63, как в примере). А если структура чисел сложнее — нам поможет таблица остатков. Так, для всех простых мы получим схожий результат, но с несколько большим периодом деления. Ниже приведён пример числа 11 (число уже в десятичном виде):
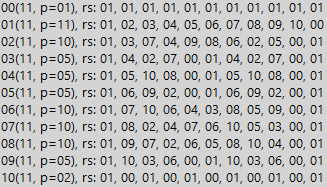
Мы видим, что в двоичной системе расстояние до нуля (период делимости) для числа 11 равно 10. То есть любое число Мерсенна, содержащее 10k единиц, где k — целое число больше нуля, обязательно делится на 11. Можно легко доказать, что остальные простые числа ведут себя точно также, кроме размера периода, разумеется. А вот для составных ситуация опять менее стройная. Ниже мы видим пример для числа 8:
Как видно, 8 не может делить числа Мерсенна в двоичном виде. Вот в троичном — пожалуйста, но числа Мерсенна состоят из единиц только в двоичном виде. Примерно так же обстоят дела и с другими составными числами — у них всё по разному. Стройная и симметричная картина для простых чисел не повторяется для составных. Но для нас важны именно простые, ведь если число делится на простое, то совершенно не проблема, если оно ещё будет делиться и на составное, включающее данное простое. А вот если число не делится на простое, то и на составное с таким простым деление окажется невозможным. Значит нас должны интересовать только простые числа.
Теперь подведём некоторый итог. Мы знаем, что числа Мерсенна делятся на простые и что для делимости числам Мерсенна необходимо количество единиц, кратное периоду делимости исследуемого числа. Но мы так же знаем, что кандидатами в простые числа Мерсенна являются лишь такие, в которых количество единиц — тоже простое число. То есть это количество не делится ни на что, кроме единицы и себя. Отсюда вывод — нам нужно такое простое число, период делимости которого равен длине числа Мерсенна. Если для какой-то длины числа Мерсенна мы не нашли делитель с подходящим периодом — перед нами простое число Мерсенна. Вроде просто.
Но дальше начинаются трудности. Как найти число, период которого совпадает с длиной числа Мерсенна? Для ответа на этот вопрос нужно решить скромную задачку — найти способ простыми средствами узнавать период для произвольного простого числа. Пока мы можем лишь делить уголком или тыкать в некоторое конкретное место при помощи формулы с большими степенями. Но если бы мы могли вычислить период без необходимости проводить долгие вычисления, то мы бы быстро подобрали нужный делитель, либо убедились бы, что таковых в природе не существует. Ровно такая же скромная задачка ждёт нас и в случае исследования делимости чисел вида 1000...000. Значит период делимости очень важен во всех отношениях.
Как найти период?
Здесь нам на помощь спешат квантовые компьютеры. Когда то давно, в некие незапамятные времена, некий знаток квантовой физики по фамилии Шор, предложил находить период именно при помощи квантового компьютера. На самом деле квантовый компьютер всего лишь даёт промежуточное значение, из которого потом обычный компьютер получает период, но суть не в этом, а в том, что без квантового компьютера пока что математика не умеет вычислять период. А вот вычислив период, мы получаем возможность прицельно вычислить значение остатка строго посередине периода. Зачем это нужно? За тем, что из него можно получить множители, обязательно содержащие некое значение, кратное делителю исследуемого числа. Это делается прибавлением к остатку единицы и вычитанием единицы. Получившиеся два числа можно пропустить через быстрый алгоритм нахождения наибольшего общего делителя с исследуемым числом. Как минимум в одном случае так мы получим делитель исследуемого числа. Правда не всё так идеально, ведь как мы видели на примере таблицы для простых чисел, посередине ряда там часто стоит дополнение до иследуемого числа (N-1), в таком виде получаем:
Из этого следует, что в одном случае имеем само исследуемое число, а с ним нет смысла вычислять наибольший общий делитель, а во втором случае имеем гарантированно не имеющее общих делителей с исследуемым числом значение. Общих делителей нет потому, что это число всего лишь на 2 меньше, чем исследуемое число, а это значит, что какое бы число не укладывалось в исследуемое целое количество раз (являлось бы его делителем), то вычтя его из исследуемого числа мы получим гарантированно меньшее значение, чем 
, или с использованием формул:
Здесь N — нечётное исследуемое число (нечётное потому что кратное двум делится на два, а нам надо, что бы ни на что не делилось), x — делитель N, k — целый результат деления 
, m — целый результат деления 
. То есть нам иногда придётся сменить систему счисления и попросить квантовый компьютер найти новый период, в надежде на то, что в его середине будет более подходящее число. Плюс ограничением является обязательность чётности значения длины периода. Но это всё не так страшно, потому что в любом случае квантовый компьютер вычислит нужную нам длину (или несколько длин) горазо быстрее, чем наступит тепловая смерть вселенной, в отличии от других алгоритмов.
Хотя вычисление периода для получения делителей числа, это несколько отличающаяся от поиска простых задача. Но тем не менее мы можем и здесь кое-что добавить с помощью таблиц остатков. Так по таблицам видно, что серединой рядов чётной длины обычно бывает число, удовлетворяющее следующему условию:
Здесь r — искомый остаток, а N — исследуемое число. Таким образом получается, что нет необходимости искать период для получения делителей числа, ведь период ищут, что бы найти тот самый остаток r, а потом добавить и вычесть из него единицу. То есть можно сразу найти этот остаток, удовлетворяющий выше приведённому условию. Правда поиск такого значени тоже нетривиален. Но может квантовый компьютер можно заточить под такое дело? Знатокам квантовых вычислений осталось понять, сколько кубит под это потребуется (кубиты — это такие попугаи, в которых измеряют «мощность» квантового компьютера). Хотя, возможно, и без квантового компьютера можно обойтись. Для этого нужно лишь понять, какие закономерности нам пригодятся. Часть закономерностей видны по таблицам остатков, ну а оставшуюся часть читателям придётся вывести самостоятельно, и тогда — вы точно взломаете криптографию на основе RSA. Правда есть пара сложностей — сначала надо найти эти полезные закономерности, ну а потом… Потом вам могут не заплатить денег. Во первых, призы дают за большие простые числа, а не за взлом RSA. А во вторых — ну сами подумайте, сколько в мире серьёзных организаций, заинтересованных в перехвате чужих данных таким образом? И вот какое-нибудь ФСБ (ЦРУ, Моссад, Ми-5, просто Мафия) узнали, что вы что-то знаете. Догадываетесь, что с вами будет? Поэтому далее вы действуете исключительно на свой страх и риск.
Правда сама квантовая тема довольно занимательна тем, что в ней присутствет квантовая неопределённость, флуктуации вакуума и прочий квантовый дарвинизм. Как это всё можно объяснить? Если честно, то я не знаю, но вижу аналогию с таблицами остатков. Например, когда кто-то наблюдает значения в таблице остатков и не знает о ранее указанных закономерностях, то для него в таблице есть лишь какой-то шум, где цифры меняют друг друга каким-то случайным образом, как некие флуктуации вакуума. Но если понять, что мы всего лишь применяем один и тот же алгоритм к разным парам «последовательность — исследуемое число», то вся эта кипящая каша из цифр моментально становится понятной. И точно так же становится ясно, почему среди огромного множества возможных значений для заполнения таблицы, в ней реально остаются лишь строго определённые. Но пока мы не получим «взаимодействие» последовательности с исследуемым числом, мы не сможем предсказать содержимое таблицы. Точнее — равновероятным будет любое её заполнение. А вот после «взаимодействия» — всё станет строго закономерным, из равновероятного родится единичная вероятность лишь для одного варианта. И не потому, что работает некий дарвинизм, а всего лишь из-за применения некоего алгоритма к конкретным входным данным. Если не знать про алгоритм, то может показаться, что ряды в таблице действительно отбираются по дарвиновски. А если знать — всё оказывается очень просто. Может и в квантовой физике нужно искать не только частицы, но и алгоритм их «деления»?
И снова про период.
Тем не менее, период очень важен для нас. Да, именно так вам ответят на горячей линии по животрепещущим проблемам математики. Как было показано выше, знание периода позволяет понять, есть ли у числа делители, или по другому — простое ли оно. Поэтому продолжим про период. Пока что мы знаем ряд свойств периода (уникальность значений, симметрия при чётной длине и т.д.), но не знаем как определить его длину. Хотя есть верхняя и нижняя границы — период не может быть длиннее исследуемого числа минус один, а так же период не может быть короче периода роста основания системы счисления до момента превышения исследуемого числа (для семи это 3, для 11 это 4, и т.д.). Можно пытаться применять известные по изученным таблицам закономерности и выводить новые, но пока что здесь видится довольно много направлений, большинство из которых не ведут к успеху, хотя пока не попробуешь каждое — не узнаешь.
Поэтому самым перспективным видится путь создания улучшенной теории делимости. На основе характеристических последовательностей остатков можно выявить закономерности делимости многих классов чисел. Пока что были показаны лишь два класса (числа Мерсенна и числа, равные степеням системы счисления), но в реальности их — бесконечное количество. Как обработать знания по всем классам чисел? Только массированной параллельной работой, и не в виде железных обогревателей воздуха, а в виде совместной работы людей над такой большой задачей. Идеальным результатом было бы именно создание общей теории делимости всех классов чисел. Это для начала, а затем уже пойдёт делимость многочленов и прочая алгебра. Но стоит ли ожидать такого чудесного массирования человеческих разумов над задачей поиска простых чисел? Подозреваю, что нет. Поэтому, как ни жаль, нам опять нужны другие пути.
Теоретически такой путь есть.
Если исследовать альтернативные делимые последовательности, включающие отличающиеся значения, то обнаружится, что период деления таких последовательностей растёт кратно длине повторяющихся фрагментов последовательностей. Ниже приведён пример делимой последовательности вида 1010...1010, где периодически меняют друг друга ноль и единица. Приведённая последовательность всегда делится на основание системы счисления, но нам в данном случае важна лишь простота примера исследования чисел периодического класса, поэтому пока не обращаем внимания на делимость «по построению».
Здесь мы видим две таблицы для числа 7 и указанной выше последовательности, одна обычная, а вторая таблица домножена на 3. От ранее выявленных закономерностей в этом примере осталось ещё меньше, но тем не менее, для систем счисления по основаниям 1 и 6 мы видим увеличение длины периода до 
. А для домноженной на 3 таблицы мы видим потерю делимости для оснований систем счисления 2 и 5, что довольно занимательно само по себе (от умножения поменялось свойство делимости). Но важнее не это. Важно понимание возможности применения таблиц делимости к любым последовательностям. Но зачем нам любые последовательности? Например, что бы увеличить минимальный период делимости.
Если минимальный период можно удлиннять, то это позволяет нам очень просто перейти к конструированию простых чисел. Да, простые числа можно не вычислять, а конструировать математически. Когда период длинный, малое число делит большое, значит если у всех чисел периоды будут большими, то у больших чисел делителями смогут быть только малые числа. Что это даёт? Это даёт возможность найти все делители большого числа простейшим перебором. Раз малые числа делят большие, то сам размер этих малых чисел помогает нашим компьютерам решать ту задачу, которую при наличии больших делителей они решить не способны. Поэтому дальнейшее направление поиска простых чисел становится понятным — нужно найти такую последовательность, которая даёт нам большие минимальные периоды. Почему минимальные? Потому что вычислять период мы по прежнему не умеем без перебора всех остатков или возведения в степень, а потому достаточно длинный период просто не сможем найти, если он больше минимального, ну а минимальный нам известен просто из анализа таблиц остатков, то есть его не нужно вычислять. Ну а когда мы найдём нужную нам последовательность (и как раз для этого нам пригодится анализ многих классов таких последовательностей), мы просто подберём такую длину последовательности, в которую не уложтся ни один из известных нам минимальных периодов. То есть мы подберём такое большое число, у которого заведомо нет делителей. И если его размер большой — нас ждёт приз. При этом периоды больше минимального нас интересовать не будут, потому что они уже делят ну совсем большие числа, до которых мы дойдём как-нибудь позднее.
Осталось всего-ничего — найти правильную последовательность. Кто возьмётся? Но даже если не найдём, то для упоминавшегося ранее шифрования работа с альтернативными последовательностями даст возможность добавить в шифр ещё одно слагаемое, повышающее криптостойкость — теперь взломщикам шифров потребуется угадать ещё и выбранную нами последовательность, которых можно насочинять бесконечное количество. Плюс для генерации псевдослучайных последовательностей мы получаем повторяемость значений ещё и в ряду остатков, а не только в ряду периода дроби.
И наконец — призы!
Electronic Frontier Foundation готова заплатить любому желающему сначала 150k$, а потом ещё 250k$. В сумме — 400k$. Вам бы не помешала эта сумма? Тогда за дело! А дело простое — нужно найти простое число длинной сто миллионов десятичных знаков. Это грубо 300 миллионов бит, или 40 мегабайт. Всего-то осталось обогнать нынешний рекорд в 4 раза. А потом вам потребуется число длинною в миллиард десятичных знаков. Это уже 400 мегабайт. И всё, за два числа — 400 тысяч вечно зелёных долларов.
На самом деле это не такие страшные цифры. Вот если бы мы могли уйти от вычисления остатка от деления больших степеней на исследуемое число… Для простых последовательностей вида 100...00 и 111...111 степень обязательно присутствует. Но может есть такие последовательности, для которых формула вычисления i-го члена ряда остатков будет попроще? Или всё же действительно удастся найти последовательность с большим минимальным периодом. Ведь какой период нам нужен? Всего-то 300 миллионов (в двоичном виде). Если некая последовательность даст нам минимальный период вида 100*N, где N — исследуемое число, то нам будет достаточно чисел до 3 миллионов, что бы найти стоящее 150k$ число. И до 30 миллионов для числа на 250k$. А сейчас, когда короткий период может случиться у очень большого числа (для последовательностей 100..00 и 111...111), мы не имеем никаких простых возможностей для его нахождения. Но надежда есть и всё зависит от удачного выбора направления поиска. Перебирать последовательности по одной, видимо, не реально для одного человека, но толпой можно попробовать.
Ну а когда найдёте требуемые числа, вас ждёт немного бюрократии. Сначала вы будете должны опубликовать статью в математическом журнале в США или Англии или Канаде или Австралии, при чём журнал должнен быть из списка, указаного Electronic Frontier Foundation (EFF) (это очень солидные журналы). В статье вы должны доказать, что ваш метод реально даёт возможность найти нужное простое число. Далее вы направляете в EFF (по определённому адресу) письмо счастья, где указываете на опубликованную статью и далее ожидаете распоряжений со стороны EFF. Распоряжения могут касаться проверки всего, что вы сделали для поиска числа. Никаких секретов быть не должно, никаких незаконных или сомнительных действий — тоже. И всё, после этого — приз ваш.
Какие засады могут вас ждать на пути? Ну для начала — найти простое число и не допустить ошибки при его поиске. Далее нужно написать в солидный журнал. Поскольку журнал солидный, то обычная реакция редакции на письмо очередного изобретателя вечного двигателя такая:
— Что? Очередной фрик? В корзину!
Но вполне возможно, что у вас есть опыт в написании статей и вы легко справитесь с этой проблемой. А далее вас ждёт проверка. Уж не знаю, какие ваши доказательства будет изучать EFF, но они пишут, что могут поинтересоваться всем, чем угодно. Особенно интересно будет, если цели EFF не совпадут с тем результатом, который вы предоставите. Так они заявляют целью разработку методов использования личных компьютеров для сдачи их во временное дистанционное пользование для сторонних вычислений. Предыдущий приз был дан как раз за создание и раскрутку программы, которую скачивали добровольцы и тем самым обеспечивали нужные террафлопсы для перемалывания простых чисел. Как EFF отнесётся к вычислению простого числа без массовых террафлопсов — я не знаю. Теоретически в их требованиях нет ограничений, поэтому успех вполне возможен.
Ну и всё, пройдя две указанные стадии (и не забыв найти нужные числа на нулевой стадии), вы указываете банк и номер счёта, куда вам капает приз. Одной большой суммой. С налоговой дальше разбираетесь за свой счёт.
Вместо эпилога.
Когда-то давно Пьер Ферма, не будучи математиком, обнаружил много закономерностей для теории чисел. Человеку было просто интересно, ну и в наличии было свободное время. И вот вам достижения, о которых помнят до сих пор. Другой пример — Эварист Галуа. Математикой занялся в 16 лет, а в 20 лет погиб на дуэли. За 4 года пытался заинтересовать своими находками многих математиков, но не преуспел. После смерти его работы всё же оценили по достоинству и именно им мы обязаны созданием такого раздела математики, как теория групп, а так же развитием алгебры. Опять же — человеку было интересно находить звёзды, а вот оформлять труды по правилам — не для него. Но к счастью его труды оформили другие. И ещё пример — Георг Кантор, размышляя над известными понятиями множества и его элемента, один вывел в конце 19-го века теорию, которую выдающиеся математики согласились считать достойной стать основой царицы наук.
К чему все эти истории? Как говаривал мистер Обама — «Ты можешь!». Да, этот американский лозунг вполне подходит для увлечённых людей. Не смотря на развитость науки сегодня, она не полна, она не идеальна, и в ней есть такие места, куда не ступала нога настоящего учёного. Поэтому давайте включим своё любопытство и попробуем поискать такие нетоптанные тропы, а вдруг и у вас получится?
Автор: math_user
