Обратные задачи аффинных преобразований или об одной красивой формуле

В этой статье я расскажу об одной необычной формуле, которая позволяет взглянуть под новым углом на аффинные преобразования, а особенно на обратные задачи, которые возникают в связи с этими преобразованиями. Обратными я буду называть задачи, требующие вычисления обратной матрицы: нахождение преобразования по точкам, решение системы линейных уравнений, преобразование координат при смене базиса и т.д. Сразу оговорюсь, что в статье не будет ни фундаментальных открытий, ни уменьшения алгоритмической сложности — я просто покажу симметричную и легко запоминающуюся формулу, с помощью которой можно решить неожиданно много ходовых задач. Для любителей математической строгости есть более формализованное изложение здесь [1] (ориентированно на студентов) и небольшой задачник вот здесь [2].

Аффинное преобразование обычно задается матрицей $inline$A$inline$ и вектором трансляции $inline$vec{t}$inline$ и действует на вектор‑аргумент по формуле

$$display$$ mathcal{A}(vec{x})=hat{A}vec{x}+vec{t}. $$display$$

Впрочем, можно обойтись и без $inline$vec{t}$inline$, если воспользоваться аугментированной матрицей и однородными координатами для аргумента (как хорошо известно пользователям OpenGL). Однако оказывается, кроме этих форм записи можно ещё использовать детерминант особой матрицы, в которой содержатся как координаты аргумента, так и параметры, задающие преобразование. Дело в том, что детерминант обладает свойством линейности по элементам любой своей строки или столбца и это позволяет использовать его для представления аффинных преобразований. Вот, собственно, как можно выразить действие аффинного преобразования на произвольный вектор $inline$vec{x}$inline$:

Не спешите убегать в ужасе — во‑первых, здесь записано преобразование, действующее на пространствах произвольной размерности (отсюда так много всего), а во‑вторых, хотя формула и выглядит громоздко, но просто запоминается и используется. Для начала, я выделю логически связанные элементы рамками и цветом

Итак, мы видим, что действие любого аффинного преобразования $inline$mathcal{A}$inline$ на вектор можно представить как отношение двух детерминантов, при чем вектор‑аргумент входит только в верхний, а нижний  — это просто константа, зависящая только от параметров.

Выделенный синим цветом вектор $inline$vec{x}$inline$ — это аргумент, вектор на который действует аффинное преобразование $inline$mathcal{A}$inline$.
Здесь и далее нижние индексы обозначают компоненту вектора. В верхней матрице компоненты $inline$vec{x}$inline$ занимают почти весь первый столбец, кроме них в этом столбце только ноль (сверху) и единица (снизу). Все остальные элементы в матрице — это векторы‑параметры (нумеруются верхним индексом, взятым в скобки чтоб не перепутать со степенью) и единицы в последней строке. Параметры выделяют среди множества всех аффинных преобразований то, которое нам нужно. Удобство и красота формулы в том, что смысл этих параметров очень прост: они задают аффинное преобразование, которое переводит векторы $inline$vec{x}^{,(i)}$inline$ в $inline$vec{X}^{(i)}$inline$. Поэтому векторы $inline$vec{x}^{,(1)},dots,vec{x}^{,(n+1)}$inline$, мы будем называть «входными» (в матрице они обведены прямоугольниками) — каждый из них покомпонентно записан в своём столбце, снизу дописывается единица. Сверху же записываются «выходные» параметры (выделены красным цветом) $inline$vec{X}^{1}, dots, vec{X}^{n+1}$inline$, но теперь уже не покомпонентно, а как цельная сущность.

Если кого‑то удивляет такая запись, то вспомните о векторном произведении

$$display$$ [vec{a} times vec{b}] = det begin{pmatrix} vec{e}_1 & vec{e}_2 & vec{e}_3\ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 \ end{pmatrix}, $$display$$

где была очень похожая структура и первую строку точно так же занимали векторы. При этом необязательно, чтобы размерности векторов $inline$vec{X}^{(i)}$inline$ и $inline$vec{x}^{(i)}$inline$ совпадали. Все детерминанты считаются как обычно и допускают обычные «трюки», например, к любому столбцу можно прибавить другой столбец.

С нижней матрицей всё предельно просто — она получается из верхней вычёркиванием первой строки и первого столбца. Недостаток (1) в том, что приходится считать детерминанты, однако если эту рутинную задачу переложить на компьютер, то окажется, что человеку останется лишь правильно заполнить матрицы числами из его задачи. При этом с помощью одной формулы можно решить довольно много распространенных на практике задач:

• нахождение аффинного преобразования по точкам;
• расчёт барицентрических координат;
• полилинейную интерполяцию;
• задачи на линейные преобразования (без трансляции):
  • обращение матрицы;
  • правило Крамера в одну формулу (нет, то что вы видели, это не в одну формулу);
  • пересчет координат вектора при изменении базиса;
  • интерполяцию полиномами Лагранжа.

Аффинное преобразование по трем точкам на плоскости

Под действием неизвестного аффинного преобразования три точки на плоскости перешли в другие три точки. Найдем это аффинное преобразование.
Для определенности, пусть наши входные точки

а результатом действия преобразования стали точки

Найдем аффинное преобразование $inline$mathcal{A}$inline$.

На самом деле, решать эту задачу можно по‑разному: с помощью системы линейных уравнений, барицентрических координат… но мы пойдем своим путем. Думаю, по использованным обозначениям Вы догадываетесь к чему я клоню: берём уравнение (1) для размерности $inline$n=2$inline$ и подставляем $inline$vec{x}^{,(i)}$inline$ в качестве входных параметров, а $inline$vec{X}^{,(i)}$inline$ — в качестве выходных

а дальше остается лишь посчитать детерминанты

Намётанный глаз легко обнаружит здесь поворот на $inline$30^{circ}$inline$ и трансляцию на $inline$((3 + sqrt{3})/2, 2)^{mathsf{T}}$inline$.

Когда формула применима?

Входные и выходные векторы могут иметь разную размерность — формула применима для аффинных преобразований, действующих на пространствах любой размерности. Впрочем, входных точек должно быть достаточно и они не должны «слипаться»: если аффинное преобразование действует из $inline$n$inline$-мерного пространства — точки должны образовывать невырожденный симплекс из $inline$n+1$inline$ точки. Если это условие не выполнено, то однозначно восстановить преобразование невозможно (никаким методом вообще, не только этим) — формула предупредит об этом нулём в знаменателе.

Зачем восстанавливать аффинные преобразования программисту?

Часто нужно найти преобразование между двумя картинками (для расчёта положения камеры, например). Если у нас найдётся несколько надёжных особых точек (фич) на этих изображениях, ну или просто не хочется начинать сразу с ранзаков и борьбы с аутлаерами, то вполне можно использовать эту формулу.

Еще один пример — текстурирование. Вырезать треугольник из текстуры и натянуть на треугольник где‑нибудь на плоскости или в пространстве — типичная задача на применение аффинного преобразования к точкам из пространства текстуры, переводящее их в пространство, где «живут модели». И довольно часто нам легко указать каким точкам на текстуре соответствуют вершины треугольника модели, но вот установить куда переходят неугловые точки может потребовать некоторых размышлений. С этой же формулой достаточно просто вставить числа в правильные ячейки и будет вот такая красота.

Из того, с чем приходилось лично сталкиваться: нейросеть выдаёт координаты углов маркера и мы хотим «дополнить реальность» виртуальным объектом, который располагается на маркере.
Очевидно, при перемещении маркера объект должен повторять все его движения. И тут формула (1) как нельзя кстати — она нам поможет передвинуть объект вслед за маркером.

Или вот еще пример: нужно запрограммировать вращение различных объектов на сцене с помощью инструмента «гизмо». Для этого мы должны уметь вращать выбранную модель вокруг трех осей параллельных осям координат и проходящих через центр объекта. На картинке показан случай вращения модели вокруг оси параллельной $inline$OZ$inline$.

В конечном итоге всё сводится к двумерной задаче о вращении вокруг произвольной точки. Давайте даже решим её для какого‑то простого случая, скажем, поворота на $inline$90^circ$inline$ против часовой стрелки вокруг $inline$(a;b)$inline$ (общий случай решается так же, просто не хочется загромождать выкладки синусами‑косинусами). Конечно, можно пойти путём самурая и перемножить три матрицы (трансляция точки вращения в ноль, собственно вращение и трансляция назад), а можно и так — найти координаты любых трёх точек до и после вращения и воспользоваться формулой. Первая точка находится легко — мы и так знаем, что $inline$(a;b)$inline$ переходит в себя. Давайте рассмотрим точку на единичку правее, для неё верно $inline$(a+1;b) mapsto (a;b+1)$inline$. Ну и ещё одну на единичку ниже, тут очевидно, что $inline$(a;b-1) mapsto (a+1;b)$inline$. Дальше всё просто

Барицентрические координаты

Разложим верхний детерминант (1) по первой строке согласно правилу Лапласа. Ясно, что в результате мы получим некоторую взвешенную сумму векторов $inline$vec{X}^{(i)}$inline$. Оказывается, что коэффициентами в этой сумме служат барицентрические координаты аргумента $inline$vec{x}$inline$ по отношению к симплексу, заданному $inline$vec{x}^{,(i)}$inline$ (за доказательствами смотреть в [1]). Если нас интересуют только барицентрические координаты точки, можно схитрить и заполнить первую строку единичными ортами — после вычисления детерминантов мы получим вектор, чьи компоненты совпадают с барицентрическими координатами $inline$vec{x}$inline$. Графически такое преобразование $inline$mathcal{B}$inline$, переводящее точку в пространство её барицентрических координат, будет выглядеть следующим образом

Давайте опробуем этот «рецепт» на практике. Задача: найти барицентрические координаты точки по отношению к заданному треугольнику. Пусть для определённости это будет точка $inline$(2,2)^mathsf{T}$inline$, а в качестве вершин треугольника возьмём

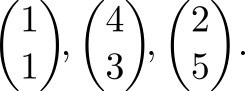
Дело за малым — взять (1) для $inline$n=2$inline$, правильно расположить там данные задачи и посчитать детерминанты

Вот и решение: барицентрическими координатами $inline$(2,2)^mathsf{T}$inline$ по отношению к заданному треугольнику есть $inline$0.6$inline$, $inline$0.3$inline$ и $inline$0.1$inline$. В программировании расчёт барицентрических координат часто возникает в контексте проверки, находится ли точка внутри симплекса (тогда все барицентрические координаты больше ноля и меньше единицы), а также для различных интерполяций, о которых сейчас пойдёт речь.

Заметьте, формула (1) обладает приятной двойственностью: если разложить детерминант по первому столбцу  — получим стандартную запись для аффинной функции, а если по первой строке — аффинную комбинацию выходных векторов.

Полилинейная интерполяция

Итак, мы обнаружили, что аффинное преобразование взвешивает выходные векторы с коэффициентами, равными барицентрическим координатам аргумента. Естественно воспользоваться этим свойством для полилинейной интерполяции.

Интерполяция цвета

Для примера, давайте просчитаем стандартный GL‑ный «привет мир» — раскрашенный треугольник. Конечно, OpenGL прекрасно умеет интерполировать цвета и тоже делает это с помощью барицентрических координат, но сегодня мы это сделаем сами.

Задача: в вершинах треугольника заданы цвета, произвести интерполяцию цвета внутри треугольника. Для определённости, пусть вершины нашего треугольника имеют координаты

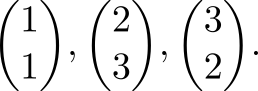
Припишем им цвета: жёлтый, циан и маджента

Тройки чисел — это RGB‑компоненты цвета. Возьмём (1) и правильно расставим входные данные

Здесь компоненты $inline$mathcal{C}(x; y)$inline$ указывают как закрасить точку $inline$(x,y)$inline$ в терминах RGB. Давайте посмотрим, что вышло.

Можно сказать, мы только что произвели аффинное преобразование двумерного пространства картинки в трехмерное пространство цветов (RGB).

Интерполяция нормалей (шейдинг Фонга)

Мы можем вкладывать самый разный смысл в векторы, которые мы интерполируем, в том числе это могут быть векторы нормалей. Более того, именно так и делается шейдинг Фонга (Phong shading), только после интерполяции векторы нужно нормировать. Для чего нужна такая интерполяция хорошо иллюстрирует следующее изображение (взятое из Википедии commons.wikimedia.org/w/index.php?curid=1556366).

Приводить расчёты, я думаю, уже не стоит — все детали рассмотрены в [2], а вот картинку с результатом я покажу.

Векторы на ней не единичные и для использования в шейдинге Фонга должны быть сначала отнормированы, к тому же, для наглядности, они направлены в очень разные стороны, что редко бывает на практике.

Найти плоскость $inline$z = z(x,y)$inline$ по трем точкам

Рассмотрим еще один необычный пример применения аффинного преобразования.
Даны три точки

Найдём уравнение проходящей через них плоскости в виде $inline$z = z(x,y)$inline$. И сделаем это с помощью аффинных преобразований: известно ведь, что они переводят плоскости в плоскости. Для начала спроектируем все точки на плоскость $inline$XY$inline$, что несложно. А теперь установим аффинное преобразование, которое переводит проекции точек в изначальные трехмерные точки

и которое «подхватит» вместе с точками и всю плоскость $inline$XY$inline$ да так, что после преобразования она будет проходить через интересующие нас точки.

Как обычно, мы лишь должны распределить числа по элементам матриц

Перепишем последнее выражение в привычном виде

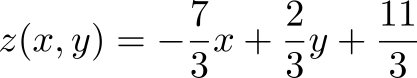
и нарисуем что вышло.

Линейные преобразования

Несмотря на всю практическую важность аффинных преобразований, чаще приходится иметь дело с линейными. Конечно, линейные преобразования — частный случай аффинных, оставляющие на месте точку $inline$vec{0}$inline$. Это позволяет немного упростить формулу (ведь один из столбцов будет состоять почти из одних нулей и по нему можно разложить детерминант)

Как видим, из формулы пропала последняя строчка с единицами и один столбец. Этот результат вполне согласуется с нашими представлениями, что для задания линейного преобразования достаточно указать его действие на $inline$n$inline$ линейно независимых элементах.

Линейное преобразование по трем точкам

Давайте решим задачу, чтобы увидеть как всё работает. Задача: известно, что под действием некоторого линейного преобразования

Найдём это линейное преобразование.

Берём упрощённую формулу и ставим правильные числа на правильные места:

Готово!

Нахождение обратного преобразования

Напомню, что матрица линейного преобразования

содержит в своих столбцах образы единичных векторов:

Итак, действуя матрицей на орты, мы получаем её столбцы. А что можно сказать об обратном преобразовании (допустим, оно существует)? Оно все делает «наоборот»:

Постойте‑ка, ведь мы только что нашли образы трёх точек под действием линейного преобразования — достаточно, чтоб восстановить само преобразование!

где $inline$vec{e}_1 = (1; 0; 0)^mathsf{T}$inline$, $inline$vec{e}_2 = (0; 1; 0)^mathsf{T}$inline$ и $inline$vec{e}_3 = (0; 0; 1)^mathsf{T}$inline$.

Не будем себя ограничивать трехмерным пространством и перепишем предыдущую формулу в более общем виде

Как видим, надо приписать к матрице слева колонку с компонентами вектора‑аргумента, сверху — строчку с координатными векторами, а дальше дело только за умением брать детерминанты.

Задача на обратное преобразование

Давайте опробуем приведённый метод на практике. Задача: обратить матрицу

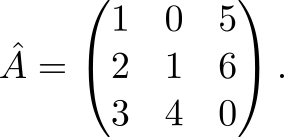
Воспользуемся (2) для $inline$n=3$inline$

Сразу видно, что

Правило Крамера в одну формулу

Ещё со школы мы сталкиваемся с уравнениями вида

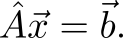
Если матрица $inline$hat{A}$inline$ невырожденная, то решение можно записать в виде

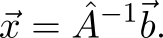
Хм… не в предыдущем ли разделе я видел такое же выражение, только вместо $inline$b$inline$ стояла другая буква? Воспользуемся им.

Это не что иное как правило Крамера. В этом легко убедиться, разложив детерминант по первой строке: вычисление $inline$x_i$inline$ как раз предполагает, что мы вычеркнем столбец с $inline$vec{e}_i$inline$, а с ним и $inline$i$inline$‑й столбец матрицы $inline$hat{A}$inline$. Теперь если переставить столбец $inline$b$inline$ на место удалённого, то мы как раз и получим правило «вставить столбец $inline$b$inline$ на место $inline$i$inline$‑го столбца и найти детерминант». И да, со знаками всё хорошо: одни $inline$pm$inline$ мы генерируем при разложении по строке, а другие при перестановке — в результате они друг друга компенсируют.

Присмотревшись к полученному уравнению, можно заметить его схожесть с уравнением для нахождения барицентрических координат: решение системы линейных уравнений— это нахождение барицентрических координат точки $inline$vec{b}$inline$ по отношению к симплексу, одна из вершин которого $inline$vec{0}$inline$, а остальные задаются столбцами матрицы $inline$hat{A}$inline$.

Решение системы линейных уравнений

Решим систему линейных уравнений

В матричной форме она выглядит так

Используем полученную формулу

откуда ответ $inline$x = 1/25$inline$, $inline$y = 14/25$inline$ и $inline$z = 2/5$inline$.

Преобразование координат вектора при смене базиса

Предположим, что мы выбрали новый базис (перешли к другой системе координат). Известно, что новые координаты векторов выражаются через старые линейно. Поэтому неудивительно, что мы можем использовать наш инструментарий для смены базиса. Как это сделать, я покажу на примере.

Итак, пускай мы перешли от стандартного базиса $inline${vec{e}_x, vec{e}_y}$inline$ к базису, состоящему из векторов

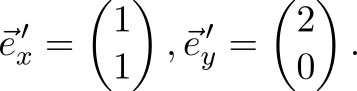
В старом базисе задан вектор $inline$vec{x}=(3,4)^mathsf{T}$inline$. Найдём координаты этого вектора в новом базисе. В новой координатной системе векторы нового базиса станут ортами и будут иметь координаты

здесь и далее штрихи возле столбцов означают, что координаты в них относятся к новому базису. Несложно догадаться, что линейное преобразование, которое переводит

также нужным образом преобразует координаты нашего вектора. Осталось только применить формулу

Решение задачи привычным образом требует обращения матрицы (которое, впрочем, также в основном состоит из вычисления детерминантов) и умножения

Мы лишь упаковали эти шаги в одну формулу.

Почему формула работает для обратных задач?

Эффективность формулы в решении обратных задач объясняется тем, что выполняется следующее равенство (доказательство есть в [1])
$

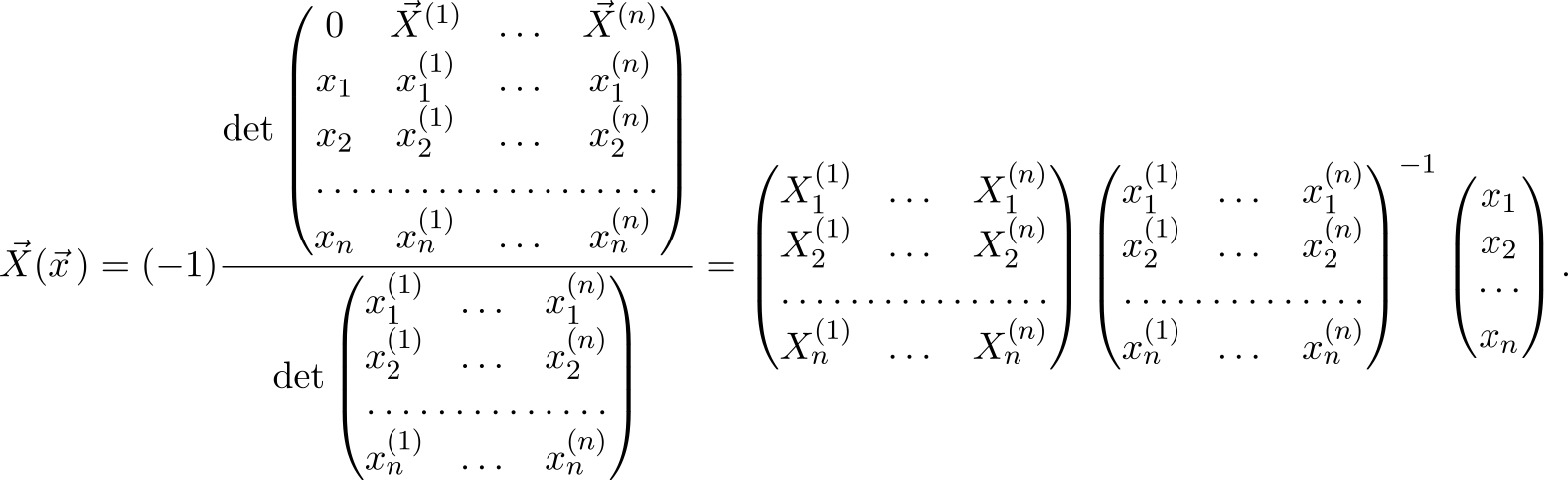
Таким образом, формула прячет в себе обратную матрицу и умножение на еще одну матрицу в придачу. Это выражение и есть стандартное решение задачи нахождения линейного преобразования по точкам. Заметьте, что делая вторую матрицу в произведении единичной, мы получим просто обратную матрицу. С ее помощью решается система линейных уравнений и задачи, которые к ней сводятся: нахождение барицентрических координат, интерполяция полиномами Лагранжа, и т.д. Однако, представление в виде произведения двух матриц, не даёт нам получить те самые «два взгляда», связанные с разложением по первой строке и по первому столбцу.

Интерполяция Лагранжа и ее свойства

Напомню, что интерполяция Лагранжа — это нахождение полинома наименьшей степени проходящего через точки $inline$(a_0; b_0)$inline$, $inline$(a_1; b_1)$inline$, $inline$dots$inline$, $inline$(a_n; b_n)$inline$. Не то чтобы это была распространённая в программистской практике задача, но всё равно давайте ее рассмотрим.

Как связаны полиномы и линейные преобразования?

Дело в том, что полином

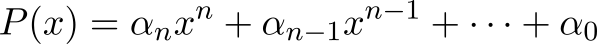
можно рассматривать как линейное преобразование, которое отображает вектор $inline$(x^n; x^{n-1}; dots; 1)^T$inline$ в $inline$mathbb{R}$inline$. Значит задача интерполяции точек $inline$(a_0; b_0)$inline$, $inline$(a_1; b_1)$inline$, $inline$dots$inline$, $inline$(a_n; b_n)$inline$ сводится к нахождению такого линейного преобразования, что

а это мы делать умеем. Подставим правильные буквы в правильные ячейки и получим формулу

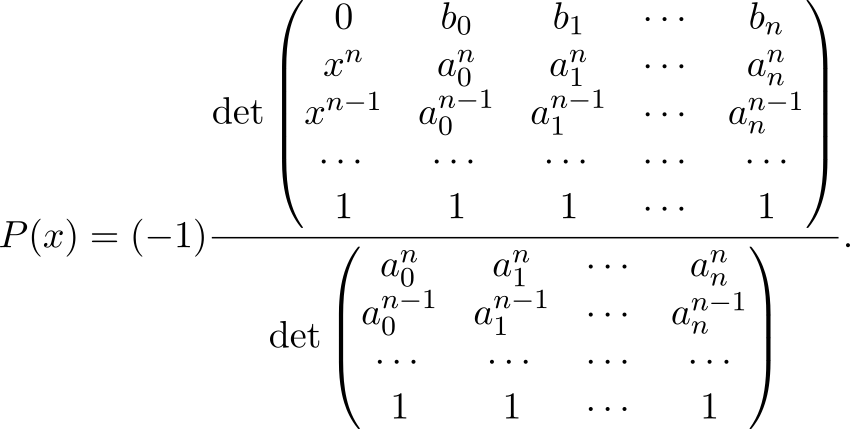
Доказательство, что это будет именно полином Лагранжа (а не чей‑то другой), можно посмотреть в [1]. Кстати, выражение в знаменателе  — это определитель Вандермонда. Зная это и разложив детерминант в числителе по первой строке, придем к более привычной формуле для полинома Лагранжа.

Задача на полином Лагранжа

Сложно ли этим пользоваться? Давайте попробуем силы на задаче: найти полином Лагранжа, проходящий через точки $inline$(-1; 2)$inline$, $inline$(3; 4)$inline$ и $inline$(2; 7)$inline$.

Подставим эти точки в формулу

На графике всё будет выглядеть так.

Свойства полинома Лагранжа

Разложив верхний детерминант по первой строке и первому столбцу, мы взглянем на полином Лагранжа с двух разных сторон. В первом случае получим классическую формулу из Википедии, а во втором — запись полинома в виде суммы одночленов $inline$alpha_i x^i$inline$, где

А ещё мы теперь можем сравнительно просто доказывать довольно замысловатые утверждения. Например, в [2] в одну строчку доказывается, что сумма базисных полиномов Лагранжа равна единице и что полином Лагранжа, интерполирующий $inline$(a_0;a_0^{n+1})$inline$, $inline$dots$inline$, $inline$(a_n;a_n^{n+1})$inline$, имеет в нуле значение $inline$(-1)^{n}a_0cdotcdotscdot a_n$inline$. Ну и не Лагранжем единым — подобный подход можно применить к интерполяции синусами‑косинусами или какими‑то другими функциями.

Заключение

Спасибо всем, кто дочитал до конца. В этой статье мы решали стандартные задачи с помощью одной нестандартной формулы. Мне она понравилась тем, что, во‑первых, показывает, что аффинные(линейные) преобразования, барицентрические координаты, интерполяция и даже полиномы Лагранжа тесно связаны. Ведь когда решения задач записываются единообразно, мысль об их сродстве возникает сама собой. Во‑вторых, большую часть времени мы просто расставляли входные данные в правильные ячейки без дополнительных преобразований.

Задачи, которые мы рассматривали, можно решить и вполне привычными методами. Однако, для задач небольшой размерности или учебных задач формула может быть полезной. Кроме того, мне она кажется красивой.

Список литературы

[1] Beginner's guide to mapping simplexes affinely

[2] Workbook on mapping simplexes affinely

Автор: Андрей Хлевнюк

Источник