Проектируем космическую ракету с нуля. Часть 1 — Задача двух тел

2019-08-08 в 17:39, admin, рубрики: diy или сделай сам, задача двух тел, космонавтика, космос, математика, проектирование, ракетостроение, ракеты

Привет всем! Сегодня я начну серию статей-лекций посвященных теме проектирования беспилотных летательных аппаратов космического назначения (ракет) =). Да-да, — вы не ослышались, самых настоящих ракет, будем их учиться проектировать по настоящему, как это (наверное) делают в каком нибудь КБ . Сам я заканчивал универ именно по этой специальности, потому некоторые знания имеются. Но сам еще ни дня в КБ (к сожалению) не проработал. По причине соответственного расположения звезд на небосводе. В общем звезды так сошлись, судьба такая у меня. Хотя мог бы уже пол года работать в КБ Южном, зимой почти устроился, осталось лишь медкомиссию пройти и сдать документы на проверку в СБУ для получения допуска секретности. Но пошло опять что то не так. До этого уже шло очень много раз, потому наверное что то накопленное выстрелило, и я решил: ~~в пе*ду~~ да ну его.

А, кстати, месяц назад послал резюме в SpaceX на mechanical engineer, но мне через два дня вежливо отказали, потому что закон ITAR. Ну попытка не пытка, а я действительно просто хотел поехать чем нибудь помочь, и никакой я не спецагент. Ну да ладно, начну пожалуй по теме, а то развел тут историю своей жизни излагать. (просто чем то нужно было заполнить начало, думал-думал — написал как есть).

Введение

Хотя моя специальность больше направлена на проектирование ракет класса «воздух-воздух», «воздух-земля», «земля-воздух», которые летают не так уж далеко (несколько десятков километров) и не так долго (меньше минуты), и «полезный груз» у них не такой уж и полезный. Особенно когда сбивают гражданские самолеты по ошибке и люди гибнут ни в чем не виноватые. Ладно технику у друг друга уничтожайте, это такое — на взрывы и разрушения приятно смотреть. Но законы Бога «возлюби ближнего своего как самого себя» нарушать — неправильно.

Так вот, хотя специализация моя не для космических масштабов, но, думаю, мы справимся. Тем более пол года или целый год, на пятом курсе проходили мимо «проектирование аппаратов предназначенных для освоения космоса». И на самом деле новое для нас там было только орбитальная механика. А в плане конструкции ракеты там даже проще, ведь им не нужно испытывать такие бешеные перегрузки в 10-20 единиц в продольном и поперечном направлении одновременно. И аэродинамика там почти неважна. Управление то только отклонением двигателей. Ну двигатели там, правда, сложнее — ЖРД. Ничего страшного, мы попробуем спроектировать космическую ракету полностью на РДТТ. РДТТ проектировать просто, пусть у твёрдого топлива и энергоемкость в два раза ниже — не страшно. Может быть получится, может и нет, это считать надо, так сразу не скажешь. По ходу разберемся. Примерно так, поехали.

Орбитальная механика

Летим мы в космос. Как летим, куда летим, когда, ~~зачем~~. На эти вопросы нам даст ответы орбитальная механика. Потому первым делом разберемся с этой штуковиной. Благо, она несложна (по крайней мере на первый взгляд). Всего то — 1, 2, 3 законы Ньютона и закон всемирного тяготения Сэра Исаака. Звезды и планеты рассматривают как материальные точки, что оправдано гигантскими расстояниями между ними по сравнению с самими их размерами.

Для примера, вот картинка в масштабе: Солнца и ближайшей к нему планеты Меркурия:

Относительные размеры Солнца, Меркурия и расстояния между ними строго соблюдены. (Черный пиксель — это Меркурий, синяя линия — траектория его движения)

А вот в масштабе вся Солнечная система:

А здесь уже и Солнце выглядит точкой, планеты и подавно.

И для полного счастья красивая картинка и Вики с относительными размерами небесных светил:

Планеты Солнечной системы

Вспомним законы Ньютона. Второй гласит, что сила $F$ , приложенная к телу массой $m$ вызывает ускорение $a$ этого самого тела в направлении силы, и притом равна произведению массы на ускорение:

$ F=ma, $

Первый закон гласит, что если на тело не действуют силы $F=0$ , то тело движется с постоянной скоростью. Или вообще не движется = движется с постоянной скоростью равной нулю:

$ ma=0, $

$ m neq 0, a=0 Rightarrow dot{v}=0 Rightarrow v=const. $

И Третий закон объясняет как взаимодействуют два тела: первое тело действует на второе с такой же силой как и второе на первое:

$F_{12}=-F_{21},$

силы равны по модулю, но направлены противоположно.

Закон всемирного тяготения выглядит так:

$F_{12}=Gdfrac{m_{1}m_{2}}{R^{2}},$

здесь $G=6,67408(31)cdot10^{-11} text{м}^{3}/(text{кг}cdot text{с}^{2})$ — гравитационная постоянная,
$m_{1}, m_{2}$ — массы первого и второго тела, $R$ — расстояние между телами.

А направлена сила от тела, на которое действует, к телу ~~девочки с каре~~, с которым происходит взаимодействие.

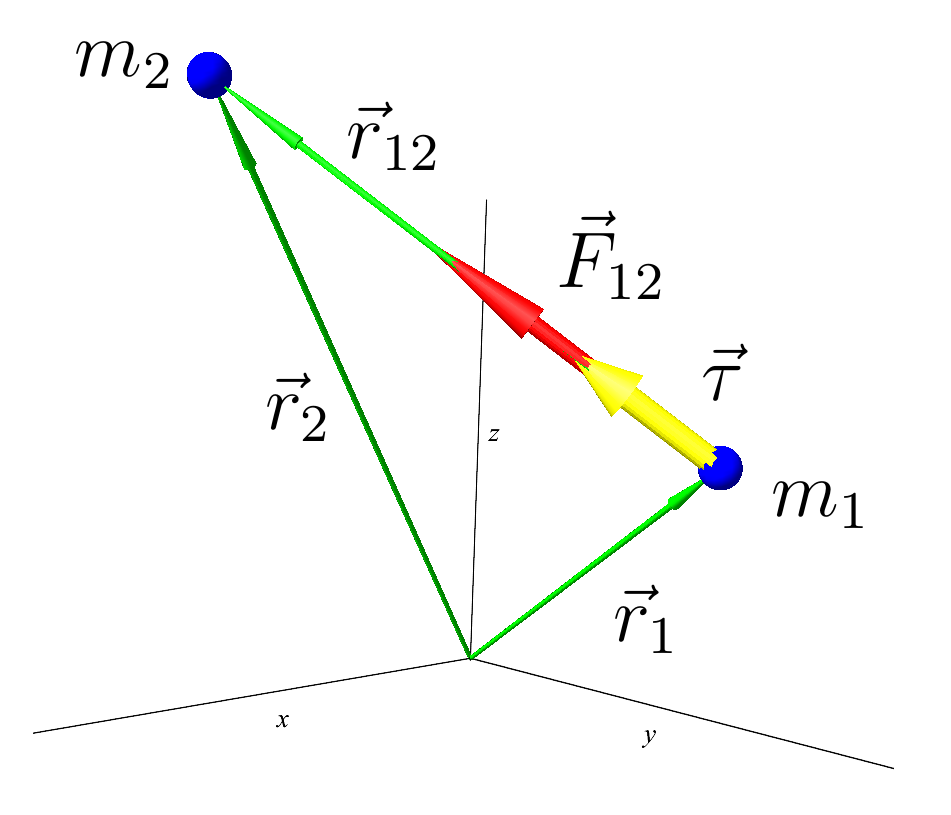
Гравитация

Теперь для двух взаимодействующих материальных точек можно записать, на основании выше записанных законов. Для первого тела:

$m_{1}ddot{vec{r}}_{1}=vec{F}_{12}=F_{12}vec{tau}=Gdfrac{m_{1}m_{2}}{R^{2}}vec{tau}, {(1)}$

здесь $vec{tau}=dfrac{vec{r}_{12}}{r_{12}}$ — единичный вектор, направленный от первого тела в сторону второго. А $vec{r}_{12}=vec{r}_{2} - vec{r}_{1}$ — из картинки видно. И $r_{12}=|vec{r}_{12}|=R$ — расстояние между телами.
Перепишем 1:

$m_{1}ddot{vec{r}}_{1}=Gdfrac{m_{1}m_{2}}{r_{12}^{2}}dfrac{vec{r}_{12}}{r_{12}}=Gdfrac{m_{1}m_{2}}{r_{12}^{3}}vec{r}_{12}.$

Для второго тела всё будет аналогично, но плюс еще по третьему закону Ньютона ( $vec{F}_{21}=-vec{F}_{12}$ ):

$m_{2}ddot{vec{r}}_{2}=vec{F}_{21}=-vec{F}_{12},$

$m_{2}ddot{vec{r}}_{2}=-Gdfrac{m_{1}m_{2}}{r_{12}^{3}}vec{r}_{12}.$

Итого для системы из двух материальных точке имеем систему дифференциальных уравнений, записанную в векторном виде:
begin{equation*}
begin{cases}
m_{1}ddot{vec{r}}_{1} = vec{F}_{12},
\
m_{2}ddot{vec{r}}_{2} = -vec{F}_{12}
end{cases}
end{equation*}
Ну что сказать, для системы из двух тел красиво получается, даже уже хочется сразу сложить эти равенства или вычесть.

Для системы же из многих N материальных точек всё будет тоже самое, но учитывать взаимодействие придется каждый с каждым. Вместо двух векторных равенств будет N штук. И у каждого справа будет сумма сил. Если пойти дальше и рассмотреть «континуум» точек, то есть сплошное тело — суммарная сила получится интегрированием по области, занимаемым телом. Всё как обычно: рассматривается бесконечна малая часть тела dV и суммируется-интегрируется. Упрощается эта процедура использованием так называемого «потенциала» силы, потому что наша сила — потенциальна, имеет потенциал, но об этом в дальнейшем поговорим, и, возможно, получим поле вокруг сферического тела. Потому что сферические тела — распространенная вещь в космосе. То что они почти сферические, и как это учитывается — тоже в дальнейшем поговорим.

А сейчас вернемся к системе из двух тел. Во первых она примечательна тем, что эта первая по сложности задача после системы из одного тела. И математически исследовать эту задачу стоит в первую очередь уже из-за этого факта. А с другой стороны, как окажется,
этой моделью можно описать $90 %$ космического движа =) (но это неточно).

Ну, например, планеты двигаются вокруг Солнца очень даже почти независимо друг от друга. Сейчас оценим это для системы Земля-Марс-Солнце. Хорошо что живем в такое время, когда достаточно в интернет отправить запрос правильный, и тебе выдает всю необходимую информацию:

масса Земли $M_{oplus}=5,9736⋅10^{24}$ кг

масса Солнца относительно Земли $M_{odot}=332940M_{oplus}$

масса Марса относительно Земли $M_{mars}=0,107M_{oplus}=dfrac{M_{oplus}}{10}$

расстояние Земли от Солнца $R_{text{С}-text{З}}=149 600 000 text{ км}=1496 cdot10^{8}text{ м}$

расстояние Марса от Солнца $R_{text{С}-text{М}}=227 900 000 text{ км}=2279 cdot10^{8}text{ м}$

Теперь то вычислить силы действующие на Землю со стороны центрального Светила и куска сферического материала, названного в честь древнеримского бога войны (сорри за поэзию, что то нашло на меня), проще простого:

$F_{text{С}-text{З}}=Gdfrac{M_{oplus}M_{odot}}{R_{text{С}-text{З}}^{2}}=Gdfrac{M_{oplus}^{2}332940}{R_{text{С}-text{З}}^{2}}$

$F_{text{M}-text{З}}=Gdfrac{M_{oplus}M_{mars}}{R_{text{M}-text{З}}^{2}}=Gdfrac{M_{oplus}^{2}}{10R_{text{M}-text{З}}^{2}}$

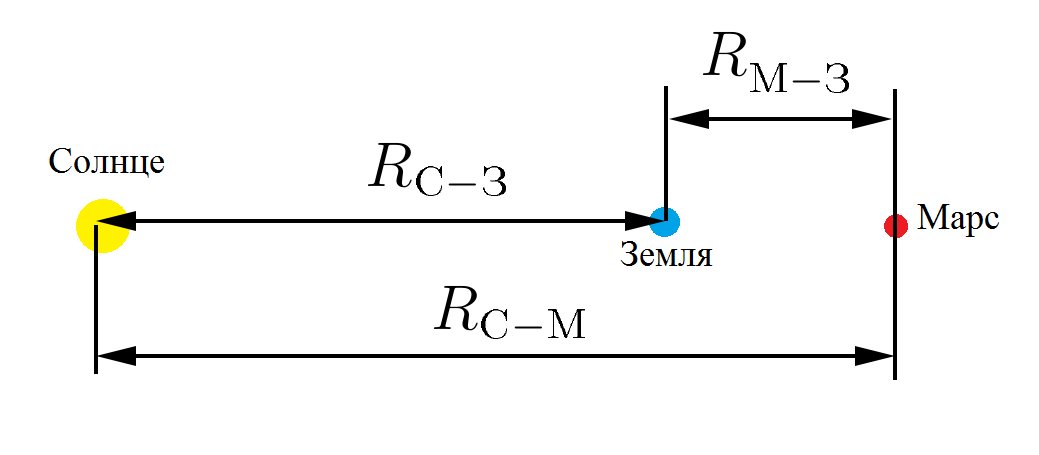
Солнце, Земля и Марс

а точнее нам не нужны даже значения этих сил, только их отношение:

$dfrac{F_{text{С}-text{З}}}{F_{text{M}-text{З}}}=Gdfrac{M_{oplus}^{2}332940}{R_{text{С}-text{З}}^{2}} cdot dfrac{10R_{text{M}-text{З}}^{2}}{G M_{oplus}^{2}}=3329400 left( dfrac{R_{text{M}-text{З}}}{R_{text{С}-text{З}}} right)^{2}=3329400 left( dfrac{R_{text{C}-text{М}} - R_{text{С}-text{З}} }{R_{text{С}-text{З}}} right)^{2},$

$dfrac{F_{text{С}-text{З}}}{F_{text{M}-text{З}}}=3329400 left( dfrac{R_{text{C}-text{М}} }{R_{text{С}-text{З}}} - 1 right)^{2}=3329400 left( dfrac{2279}{1496} - 1 right)^{2}=$

$=3329400 cdot 0.5234^{2}=912 066.1$

Ого. Практически в миллион раз сильнее Солнце притягивает Землю, чем Марс в лучшие свои годы. В смысле когда Марс-Земля-Солнце расположены на одной прямой. При другом расположении Марс будет притягивать еще хуже. Ну даже не знаю какую аналогию привести, может быть это как отношение сил веса одной монетки против Тираннозавра.

Так же дела обстоят и со всем остальным небесным воинством Солнечной системы: Солнце влияет на каждую особь, в то время как они друг на дружку почти не влияют. Я попарно не проверял, но думаю это так. Наверное, это есть следствие в том числе и того, что масса солнечной системы равна:

$1,0014M_{odot}=M_{odot} + 0,0014M_{odot},$

то есть вся масса сосредоточена в Солнце, а $0.14%$ солнечной массы — планеты, кометы, газ и всякий мусор.

Вторым примером, где нам поможет модель из двух тел — движение искусственного спутника вблизи Земли. Здесь аналогично, Земля имеет колоссальную массу по сравнению со спутником. И даже можно привести еще один наглядный пример вычислений системы Земля-спутник-Луна. На спутник действуют силы:

$F_{text{Сп}-text{З}}=Gdfrac{M_{oplus}M_{text{Сп}}}{R^{2}},$

$F_{text{Сп}-text{Л}}=Gdfrac{M_{leftmoon}M_{text{Сп}}}{R^{2}}=Gdfrac{M_{oplus}M_{text{Сп}}}{81R^{2}},$

просто масса Земли в 81 раз больше массы Луны. А расстояние здесь мы взяли пополам, то бишь середина между Землей и Луной. И наконец отношение этих сил:

$dfrac{F_{text{Сп}-text{З}}}{F_{text{Сп}-text{Л}}}=81$

Вывод: даже когда спутник будет летать ровно между Землей и Луной, а это орбита 192 200 км, Земля всё равно будет притягивать наш искусственный спутник в 81 раз сильнее Луны. Для сравнения изобразим это двумя векторами сил рядом расположенными, длинны которых будут отличатся в 100 раз. Здесь мы просто округлили по инженерному, потому что для инженера — 80 это то же самое что и 100. Это типа известного инженерного равенства, кто не в курсе: $pi=e=2. $

Сравнение сил действия на спутник со стороны Земли и Луны