Добрый день, дорогой читатель! Это вторая переводная статья из цикла статей о создании физического движка авторства Chris Hecker. Если Вы ещё не ознакомились с первой, то рекомендую это сделать, т. к. всё сразу станет понятнее. Большое спасибо за поддержку первого перевода: это очень стимулирует работать дальше и больше! Приятного чтения!
Физика, часть 2, угловые эффекты
Только что я захотел подпереть дверь чем-нибудь тяжёлым, чтобы ко мне не вошёл злоумышленник. Неужели я многого прошу? Я хочу, чтобы его машина перевернулась и взорвалась в определенным месте. Я хочу, чтобы огромные шестерни заело перед тем, как меня расплющит. И я хочу наспех построить штуку, похожую на качели, для того, чтобы катапультировать милый пылающий подарок через крепостную стену замка. Кто же может мне помешать воплотить это всё в реальность? Вы предположите, что мой соперник в игровом мире, но в действительности – программист физического движка, потому что в основе всего вышеперечисленного лежит угловой эффект. Можно пересчитать по пальцам те игры, где реализованы угловые эффекты, не говоря уж о том, чтобы найти хотя бы одну, в которой это сделано правильно.
Основная причина, почему угловые (или иначе вращательные) эффекты не реализованы в играх на сегодняшний день – это то, что программисты считают, что физика, описывающая вращательное движение, слишком сложная для понимания и воплощения в реальность. На уроках физики в старшей школе (где мы все узнали второй закон Ньютона) обычно не рассказывают о вращательных эффектах, и это не совсем очевидно, как перейти от силы, приложенной к объекту, ко вращению этого объекта. Конечно, динамика вращательного движения немного труднее для понимания, чем динамика линейного движения, но она проще, чем кажется. Любой, кто может создать физический движок в соответствии с тем материалом, что представлен в первой статье цикла, справится и с тем, чтобы включить в него угловые эффекты, описанные в этой статье. Есть надежда, что после публикации данной статьи мир наполнится играми, которые используют все возможности и преимущества угловых эффектов, или, по меньшей мере, вы сможете создать игру, в которой вы, выгнувшись, выстрелите в ногу вашего друга в смертельном бою.
Краткое повторение
Несмотря на то, что каждая моя статья на какую-то единственную тему, я всегда перечитываю то, что написал ранее, для того, чтобы понять, где закончил. Я только что посмотрел свою первую статью о физике, и я в восторге: мы успели выучить так много, и притом, ни разу не писали программный код и не читали дополнительную литературу! Прежде, чем начнем, давайте освежим в памяти материал из последней статьи.

Таблица 1 содержит важнейшие выводы для динамики твердых тел. Из Уравнения 1 следует, что вектор коодинаты ( r ), вектор скорости (v), и вектор ускорения (a) связаны производными (и интегралами, если читать в обратном порядке). Как напоминание – мы отмечаем дифференцирование по времени штрихом (r’). r’ – это то же самое, что dr/dt, а r’’ – это то же, что и вторая производная по времени. Из Уравнения 2 следует, что сила связана с линейным импульсом (произведение массы на скорость), массой, и ускорением. Определение центра масс можно почерпнуть из Уравнения 3 (это точка, где все массы и расстояния уравновешивают друг друга). Уравнение 4 гласит, что полный линейный импульс твердого тела – это сумма всех его импульсов, которые, к нашей удаче, просто равны импульсу центра масс (CM). Уравнение 5 – это настоящий драгоценный камень. В нем используется Уравнение 4 для демонстрации того, что ускорение центра масс объекта связано с полной силой (вектором суммы всех сил, действующих на объект в данное время) посредством скалярной величины, массы объекта.
Подведем итоги всему, что описано в первой статье: мы узнали, что общая сила, действующая на наш центр масс, равна сумме всех сил, приложенных к телу (включая силу гравитации, фуру злодея, взрыв неподалёку, импульс тяги нашего двигателя и т. д.). После мы разделили этот вектор суммы на массу тела для того, чтобы получить ускорение CM, и затем интегрировали ускорение по времени, чтобы получить скорость и координату тела.
Уравнение 5 – это просто шедевр! Обратите внимание, что в нем нет указаний на то, как направлены силы, действующие на тело, а это является ключевым моментом для определения, как тело будет вращаться под их действием. Уравнение 5 правильное. В действительности, оно превосходно подходит для нахождения линейного ускорения. Мы уже находимся в середине нашего пути. Но всё по порядку…
Каков твой угол?
В первой статье игнорировалось вращение, поэтому нам были необходимы лишь вектор координаты и его производная для описания конфигурации нашего тела в 2D. Теперь добавим еще одну величину кинематики, ориентацию (обозначается заглавной буквой омега – Ω), для того, чтобы работать с угловыми эффектами. Для того, чтобы задать Ω, нам необходимо выбрать систему координат относительно твёрдого тела и систему координат игрового мира, и величина Ω будет равна разнице углов между ними в радианах, как показано на Рисунке 1.
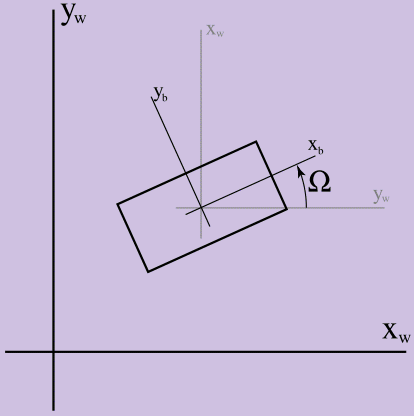
Рисунок 1. Определение Ω
На рисунке оси xw, yw – оси координат игрового мира, а xb, yb – оси координат твердого тела. Ω больше 0, если считать против часовой стрелки. Здесь важно прояснить, почему мы изучаем динамику двумерного мира прежде, чем перейти в трёхмерный: ориентация в 2D – это скалярная величина (угол между системами координат в радианах), тогда как определение ориентации в трехмерном мире гораздо труднее.
По ходу того, как тело вращается, величина Ω изменяется. Это изменение приводит нас к другой величине кинематики – угловой скорости (обозначается строчной буквой омега – ω). В отличие от координаты и линейной скорости тела, мы не обозначаем угловую скорость следующим образом – Ω’. Тем не менее, иногда мы обозначаем производную скорости по времени, или угловое ускорение, как ω’ (это еще одна величина кинематики) или как α (строчная альфа). Не вините меня: не я придумал все эти обозначения; и в каждой книге, что я прочел, имеются небольшие расхождения. Наш угловой аналог для Уравнения 1 – это:
$$display$${d^2 Ω over{dt^2}} = {dω over {dt}} = ω'= α$$display$$
Уравнение 6
Как и в Уравнении 1, мы дифференцируем ω по времени, чтобы получить α; и если мы интегрируем α по времени, получаем ω и т. д. Все по аналогии с предыдущей статьей: зная угловое ускорение α, мы можем дважды проинтегрировать его, чтобы получить новую ориентацию. Но ключевой момент здесь – надо знать величину α.
Как можно предположить, наша цель на эту статью – вывести угловой аналог для каждого из линейных уравнений в Таблице 1, и затем, учтя линейные и угловые уравнения и силу, приложенную к объекту, мы можем подсчитать его линейное ускорение a и угловое ускорение α. Наконец, мы можем численно проинтегрировать эти ускорения для нахождения новых позиции и ориентации нашего тел.
Для начала свяжем линейные и угловые величины вместе. А это довольно неочевидная проделка, в которой используется угловая скорость. При подсчетах в динамике нам нередко надо найти скорость произвольной точки объекта. Например, когда мы рассчитываем столкновения твердых тел, надо знать скорость столкнувшихся точек для того, чтобы понять, как сильно они ударили друг по другу. Если наши тела не вращаются, скорость каждой точки тела одинакова. Мы можем просто следить за скорость центра масс тела, и этого будет достаточно. Тогда как если наши тела вращаются, каждая точка этих тел может иметь разную скорость. Очевидно, что мы не можем просчитывать скорость бесконечного количества точек нашего твердого тела, поэтому нам необходимо иное, лучшее решение.
Один из простых способов, которые применяются для нахождения линейной скорости любой точки внутри объекта, использует угловую скорость объекта. Рассмотрим случай, когда тело вращается лишь вокруг одной зафиксированной точки O, без изменения координаты тела. Т. е. тело вращается, но не перемещается. Из Уравнения 7 следует, как вычислить скорость точки B вращающегося тела:
$$display$$v^B = ωr^{OB}_⟂$$display$$
Уравнение 7
Надо прояснить пару моментов в Уравнении 7, давайте потратим на это немного времени. Во-первых, я использую верхнюю индексацию для того, чтобы показать, какой параметр принадлежит к данным точкам, поэтому v^B – это вектор скорости точки B нашего тела. Аналогично r^OB обозначает вектор, проведенный из центра вращения нашего тела O в точку B. Забавная перевернутая буква T – это символ перпендикуляра, который строится на векторе (как то вектор r в Уравнении 7) и разворачивает его на 90 градусов против часовой стрелки. Другими словами, строится новый вектор, перпендикулярный старому. В двумерном мире вектор, перпендикулярный (x, y) – это просто (-y, x). Вы можете легко проверить мои слова на листе миллиметровки. Поговорим побольше об этом. Величина перпендикулярного вектора определяется угловой скоростью ω и задает линейную скорость v^B. Говоря русским языком, Уравнение 7 показывает, что скорость точки на вращающемся теле вычисляется измерением перпендикулярного вектора, направленного из центра вращения в точку с данной угловой скоростью. Как я это понял? Что ж, я прочел об этом в книге, но, очевидно, что такого объяснения недостаточно, поэтому докажем, что это истина.
Докажем истинность выводов из Уравнения 7 в два этапа. Сначала докажем, что величина результирующего вектора скорости правильная; затем – что его направление правильное. Для первой части доказательства рассмотрим Рисунок 2.
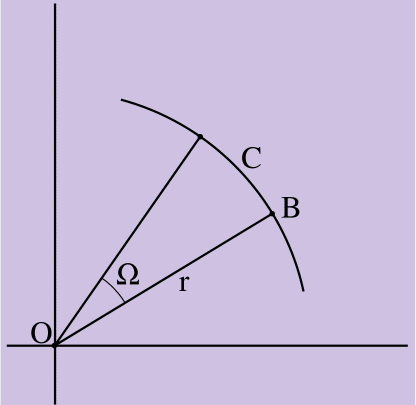
Рисунок 2. C = Ωr
Рисунок 2 демонстрирует вращение точки B на угол, равный Ω радиан по ходу вращения твердого тела с радиус-вектором длины r, направленным из центра вращения тела O в точку B. B прошла длину дуги C, где C = Ωr из определения радианов. (Радианная мера угла – это мера дуги, ограниченной радиусом окружности. Длина окружности C = 2πr, потому что радианная мера дуги окружности – это 2π [или 360 градусов]).
Скорость точки – это изменение ее координаты по времени. Поэтому мы можем найти скорость точки B – иными словами, величину вектора скорости – дифференцируя уравнения движения по времени. С = Ωr –это уравнение движения.
Радиус выносится за знак дифференцирования, т. к. это константа (B – это обычное вращение, без перемещения), и производная Ω по времени – это ω из Уравнения 6. Поэтому величина вектора B – это вектор скорости ωr.
По рассмотрении Уравнения 7 мы заметим, что величина вектора скорости правильная, т. к. перпендикуляр никак не влияет на длину вектора и r^OB – это радиус-вектор, направленный из O к B. Фух, мы на полпути.
Для того, чтобы удостовериться в правильности направление вектора скорости в Уравнении 7, начнем того, что убедимся в том, что вектор скорости должен быть перпендикулярен к радиус-вектору. Это предположение понятно интуитивно, потому что точка, вращающаяся вокруг какой-либо другой заданной точки, может двигаться только перпендикулярно вектору между этими точками. Она не может приблизиться к центру вращения или отдалиться от него, или это движение попросту перестанет быть вращением. Можем подкрепить наше предположение расчетами для векторов, но я зажат в определенные рамки по объему статьи, поэтому будем считать, что наше предположение правильное. (Если вы горите желанием доказать это самостоятельно, продифференцируйте скалярное произведение длины вектора на себя.)
Наконец, мы должны убедиться, что вектор обозначен правильно, т. к. на рисунке представлены два вектора, равной длины, перпендикулярных радиусу: v и -v. Т. к. величина Ω измеряется против часовой стрелки, ω > 0, когда точка вращается по часовой стрелке. Перпендикуляр указывает в направлении по часовой стрелке, как и радиус-вектор. На Рисунке 3 демонстрируются выводы из Уравнения 7:
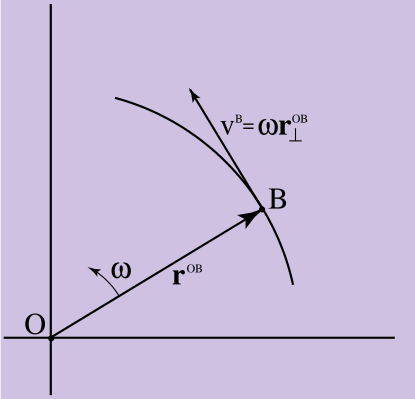
Рисунок 3. Связь линейной скорости и угловой
Дополним Уравнение 7, чтобы оно описывало вращение движущихся тел. Рассмотрим движение твердого тела, как простое перемещение центра вращения тела и простое вращение остальной части тела вокруг этой точки. Для тех, кому интересно, это Теорема Шаля о классификации движений.
Теорема Шаля разбивает наше движение на две составляющие – линейное и угловое. Пусть центр вращения тела O – это единственная перемещающаяся точка, затем используем ω, для вычисления вращения вокруг точки O, и это дает нам общую форму Уравнения 7:
$$display$$v^B = v^O+ ωr^{OB}_⟂$$display$$
Уравнение 9
Уравнение 9 гласит, что мы можем подсчитать скорость любой точки движущегося тела, используя линейную скорость точки вращения тела и, в дополнение к этому, скорость, приобретенную при вращении тела.
Повод для нашего импульса
Сейчас мы можем написать угловой аналог Уравнения 2, уравнения силы. Начнем с определения момента импульса, L^AB данной точки B, вокруг другой точки A:
Уравнение 10
Момент импульса точки отличается от линейного момента точки тем, что в угловой версии уравнения учитывается позиция тела в пространстве. Из этого следует, что момент импульса точки должен измеряться для иного места игрового мира, в отличие от линейного импульса, который определяется для заданной точки (произведение её массы на скорость). Это показано через верхнюю индексацию в Уравнении 10. Запись L^AB гласит, что момент импульса измеряется для точки B от точки A (центра вращения тела). Представьте стрелу, направленную из точки A в точку B. Эта стрела – радиус-вектор между двумя точками, обознается r^AB. Итак, момент импульса точки – это скалярное произведение вектора линейного импульса и перпендикулярного ему радиус-вектора. Это называется «скалярное произведение», и является 2D аналогом для векторного произведения 3D, но его мы обсудим в другой раз.
Если графически изобразить то, что следует из уравнения 10, на бумаге – как я и сделал на Рисунке 4 – вы увидите, что оно определяет меру того, как линейный момент точки B «вращается вокруг» A.
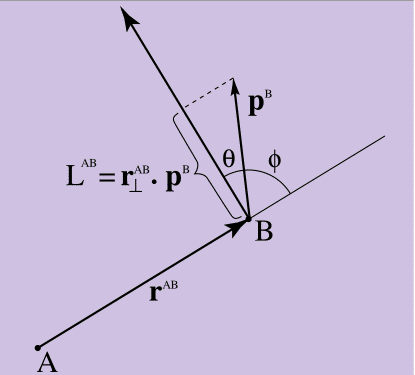
Рисунок 4. Момент импульса
Все корректно, если линейный импульс точки B вращается в правую сторону относительно точки A, Уравнение 10 = 0 (т. к. перпендикуляр к r формирует прямой угол с p, и скалярное произведение будет равно 0). Чем больше величина импульса B, направленная перпендикулярно к A, тем больше величина момента импульса. Как можно увидеть на Рисунке 4, скалярное произведение в Уравнении 10 имеет в качестве параметра косинус угла θ, заключенного между перпендикуляром r^AB к p^B. Если же посмотреть на это с другой стороны, величина скалярного произведения задается синусом угла φ между первоначальными, не перпендикулярными r^AB и p^B (синус – это еще один ключ к разгадке связи между векторным и скалярным произведением). В любом случае, из Уравнения 10 следует то, в какой мере линейный импульс B находится во «вращающемся направлении» по отношению к A.
Также, как мы использовали производную линейного импульса для определения силы, мы будем использовать производную момента импульса для определения углового близнеца силы – момента силы (обозначается строчной буквой тау – τ).
Уравнение 11
Для экономии места я немного смухлевал в Уравнении 11, пропустив пару трудных шагов, которые включают в себя нахождение производных. Из всего вышесказанного следует, что момент силы связан с силой в определенной точке посредством скалярного произведения.
Наконец, мы получили уравнение динамики, в котором используется точка приложения силы, которая ранее игнорировалась в уравнениях линейного импульса. В Уравнении 11 используется скалярное произведение, как величина силы, приложенной в точке B, находится во «вращении вокруг» точки A; эта «вращательная сила» называется моментом силы. Уравнение 11 позволяет найти численное значение момента силы – и отсюда угловой момент, если мы проинтегрируем момент силы, зная приложенную силу и точку приложения.
Тем не менее, мы до сих пор не получили уравнение связи момента силы и угловых величин кинематики, которые необходимы нам для вращения объекта вокруг своей оси – таких как угловое ускорение, угловая скорость или ориентация. Поэтому мы не можем продвинуться дальше до того, как выведем еще несколько уравнений.
Момент, которого мы все так ждали
Перед тем, как провести связь между величинами динамики и кинематики, надо дать определение полному моменту импульса, по аналогии с тем, как мы определяли полный линейный импульс в Уравнении 4. Я не забыл об угловом эквиваленте для центра массы в Уравнении 3; мы увидим его в уравнении полного момента импульса.
Полный момент импульса около точки A обозначается L^AT и определяется Уравнением 12:
Уравнение 12
Уравнение 12 – это сумма всем моментов импульса всех точек тела, измеренная относительно точки A. В правой части я использовал определение линейного импульса для того, чтобы представить p^i как произведение массы на скорость (mv). Это пригодится мне в будущем для того, чтобы сделать из Уравнения 12 что-то с более выраженным прикладным характером. Уравнение гласит, что для нахождения полного момента импульса для нашего объекта, необходимо просуммировать моменты импульса всех его точек. Для твердого тела, состоящего из граней (а не из отдельных точек), необходимо вычислить интеграл, на не дискретную сумму.
К счастью, можно упростить наши вычисления, введя новую величину под названием «момент инерции», аналогично тому, как мы ввели центр масс для упрощения уравнения полного импульса. Вспомним о том, что благодаря Уравнению 7 мы можем найти скорость точки через угловую скорость. Пусть точка A в Уравнении 12 – это цент вращения из Уравнения 7, и индекс суммирования i в Уравнении 12 – это точка B из Уравнения 7, то возможно преобразовать Уравнение 7 в Уравнение 12. Получим:
$$display$$L^{AT} = sum _{ i} {vec r ^{Ai} times m^i ω vec r^{Ai}} = ω {sum _{ i} {m^i vec r^{Ai} times vec r ^{Ai}}} = ω sum_{ i} {m^i (vec r ^{Ai})^2} = ωI^A$$display$$
Уравнение 13
Распишу Уравнение 13 подробнее, шаг за шагом. Сначала заменим Уравнение 7 на 12 для того, чтобы получить сумму в Уравнении 13. Эта замена позволяет нам описать момент импульса, используя угловую скорость. Далее выносим ω за сумму, потому что она равна для всех точек твердого тела (угловая скорость определяется для всего тела, а не для каждой его точки в отдельности), и запишем массу с индексом i слева, для того, чтобы яснее видеть скалярное произведение радиус-вектора на себя. Это скалярное произведение равно квадрату длины радиус-вектора (скалярное произведение любого вектора на себя = квадрату его длины. Запомните, что перпендикуляр не изменяет длину вектора.). Наконец, запишем I^A для того, чтобы обозначить момент инерции вокруг точки A.
Момент инерции для двумерного твердого тела – это чрезвычайно хорошее число, потому что точки, составляющие тело, не могут изменить свою массу или отдалиться от центра вращения. Как следствие из этих двух свойств, сумма в Уравнении 13 – это константа для каждого тела, поэтому мы можем подсчитать ее. Говоря по-русски, I^A – это сумма расстояний в квадрате от точки A ко всем остальным точкам тела, и каждое такое расстояние масштабируется в соответствии с массой каждой точки. Совсем, как для центра масс – если тело скорее сплошное, чем составленное из дискретных точек, то суммы превратятся в интегралы. А момент инерции останется таким же по величине и будет иметь тот же физический смысл.
Определение момента инерции около какой-либо точки многословно, но подумайте об I^A как о мере того, насколько тяжело повернуть тело около точки A. Например, представьте себе карандаш (плоский карандаш). Если измерить момент инерции около центра карандаша, получим определенную величину, равную сумме квадратов расстояний, масштабируемых в соответствии с массой каждой точки. Тогда как если мы измерим инерцию на около кончика того же карандаша, получим бОльшую величину, потому что чем дальше удалены точки с массой, тем больше значение квадратов их расстояний. Здесь будет сформулировано математически то, что понятно нам интуитивно: вращение карандаша вокруг его центра намного проще (читай тратит меньше сил), чем вращение его же вокруг одного из концов.
Наконец-то мы готовы провести связь между угловыми уравнениями динамики и угловыми уравнениями кинематики. Если мы дифференцируем Уравнение 13, получим общий момент силы слева, и произведение момента инерции на угловое ускорение справа (I^A – это константа, вынесем ее за знак дифференцирования):
$$display$$τ^{AT} = {dL^{AT} over dt} = {d( I^A ω) over dt} = I^A ω = I^A α$$display$$
Уравнение 14
Это уравнение – угловой эквивалент Уравнения 5; по факту, это F = ma для угловой динамики. Это уравнение связи полного момента силы и угловое ускорение тела посредством скалярного момента инерции. Если мы знаем момент силы, оказываемой на наше тело, мы можем найти его угловое ускорение, а дальше – угловую скорость и ориентацию в пространстве посредством интегрирования – поделив момент силы на момент инерции.
Алгоритм динамики
Он с трудом видится нам через этот вихрь уравнений, но все они – его составная часть. Мы вывели достаточно уравнений для того, чтобы получить великолепную динамику двумерного мира с произвольно заданными силами и моментами сил, перемещающими и вращающими наши объекты. Как же использовать эти уравнения? Ниже представлен базовый алгоритм:
- Найти величину центра масс и момент инерции в центре масс.
- Задать начальные координаты тела, его ориентацию в пространстве, его линейную и угловую скорости.
- Учесть все силы, действующие на тело и точки их приложения.
- Найти равнодействующую всех сил и разделить ее на массу тела для того, чтобы найти линейное ускорение центра масс (Уравнение 5).
- Для каждой силы найти скалярное произведение между вектором, направленным из центра масс в точку приложения силы, и вектором приложенной силы, добавить эту величину в полный момент силы в уравнении центра масс (Уравнение 11).
- Найти частное для полного момента силы и момента инерции в центре масс для нахождения углового ускорения (Уравнение 14).
- Численно интегрировать линейное ускорение и угловое ускорение для обновления координаты, линейной скорости, ориентации в пространстве и угловой скорости (смотри последнюю статью).
- Отрисовать объект в полученной координате, и перейти к Шагу 3.
В алгоритме выше есть лишь два шага, которые я не объяснил. Во-первых, как подсчитать момент инерции в Шаге 1 для сплошного объекта? Во-вторых, как решить проблему с силами из Шага 3? Ответ на первый вопрос может быть найден в простом примере кода, который я оставлю в приложении в конце этой статьи (вы выполните интегрирование объекта по его площади). Множество книг по динамике содержат рассчитанный момент инерции для часто встречающихся форм объектов в приложении в самом конце, поэтому вам не придется каждый раз выводить их самостоятельно.
Ответ на вопрос, как подсчитать силы из Шага 3, зависит от приложения, но немного общих рекомендаций я дам. Во-первых, такие силы, как гравитация, всегда направленные в одну сторону (вниз, в случае с гравитацией), не создают момент силы, т. к. они тянут все точки в одно и то же время в одном направлении, хотя мы и прикладываем эти силы напрямую к центру масс. Силы, подобные силе упругости, приложены к определенной точке объекта, они создадут момент силы, поэтому рассматриваем их в общем случае. Как мы увидели в первой статье, сила трения – это та же сила, направленная в противоположную от скорости тела сторону.
Вы можете сделать простую физическую модель, демонстрирующую силу трения, и просто приложить силу к центру масс, или вы можете выбрать, к каким частям объекта будут приложены силы трения, и сделать это, что может создать момент силы, действующий на объект. Силы, которые тела испытывают при столкновениях, немного труднее, и мы познакомимся с ними в следующей статье. Силы, подобные тяге ракетного двигателя, нужно рассматривать, как силы с точкой приложения (вы этом случае, если один из двигателей откажет, вы начнете крутиться вокруг своей оси до тех пор, пока не отрегулируете руль, чтобы обеспечить уравновешивание момента силы!). Если вы хотите что-то, похожее на гравитационные лучи из НЛО, то эта сила должна рассчитываться, как сила гравитации и не создавать момент силы, или она должна быть приложена к определенной точке объекта, и он будет вращаться вокруг этой точки, пока поднимается ввысь? Выбор за вами. Ключевой момент – не бояться экспериментировать с различными силами, рассчитанными разными способами, ведь уже сейчас у вас есть настоящий симулятор двумерной графики, попробуйте разные виды сил!
Я оставил весь необходимый вам код и ссылки на своем веб-сайте, потому что здесь закончилось свободное место. В своем простом приложении я воплотил в жизнь алгоритм динамики двумерного мира, а также добавил объекты, скрепленные пружиной; они вращаются вокруг своей оси, и иногда даже сталкиваются со стенами, крутсясь. Но об этом я расскажу в другой раз. Перейдите по ссылке за дополнительной литературой и простым приложением для Windows 32 и Macintosh.
Очень редко Chris Hecker испытывает на себе действие момента инерции, но обычно это проходит и довольно быстро. Силы можно прикладывать к checker@bix.com.
Примечания переводчика: здесь представлена игра слов, обыгрывается тема статьи и ее содержание.
P.S. Обратная связь приветствуется. Ваши комментарии позволяют повысить качество работ. Спасибо!
Автор: Enthusiastic_programmer





