Здравствуй, уважаемый читатель! Представляю вашему вниманию перевод с английского языка статьи «Physics, The Next Frontier» авторства Chris Hecker.
Я, начинающий Java-разработчик, столкнулся с тем, что материалы по созданию физического внутриигрового движка представлены лишь на английском языке, поэтому и была переведена данная статья. В серии будет ещё три статьи, я буду выкладывать их по мере готовности. Приятного чтения!
Новые рубежи в Физике
Нет никаких сомнений в том, что с каждым годом внутриигровая графика становится всё реалистичнее. Уже сегодня каждый создаёт (или по меньшей мере показывает скриншоты) 3D миров с картами текстур, и когда достаточно трудолюбивые люди собираются вместе для работы над одним проектом, каждый разработчик может отрисовывать миллиарды полигонов реалистичных текстур и теней в секунду. Говоря техническим языком, что же остаётся сделать для создания игры на высоком уровне? Будет ли каждый разработчик с копией книги «Learn to Use 3D Hardware in 21 Days» в состоянии создать поистине впечатляющую игру?
Отнюдь нет. Высококлассные разработчики продолжат поднимать планку во множестве различных технологий (таких как сложность графического интерфейса, искусственный интеллект и создание сетей). Конечно, всё это очень важно, мы даже не можем серьёзно обсуждать любую из них без уточнения деталей. Тем не менее, существует одна применимая ко всему технология, которая, по моему мнению, станет решающим фактором в ближайшем будущем: физика.
Рассмотрим следующий пример: вы помните эти громадные вращающиеся шестерни в свободно распространяемых уровнях игры «Duke Nukem 3D»?

Рисунок 1. Скриншот из игры «Duke Nukem 3D»
Просто представьте, что их вращение описывалось бы не gif-анимацией, а реальным физическим движком. Внезапно шестерни становятся чем-то большим, чем игровое украшение, сразу как одна из них отклоняется от заданного угла, и скатывается вниз по коридору за вами, в стиле Индиана-Джонса. Или вообразите, что после выстрела по шестерне из ракетницы, она покатится вниз по коридору и раздавит вашего друга, подкравшегося сзади, чтобы убить вас! Физические двигатели делают подобные ситуации реальными.
Физическая симуляция – это то, что делает мир цельным: благодаря ей «здесь» находится именно здесь, если вы понимаете, о чём я. Любая магия в графике в мире не позволит игроку погрузиться в игровой процесс, если он будет взаимопроникать в другого игрока, или в стены уровня, или если не будет чувствоваться масса и момент массы. Оригинальные аниматоры в компании «Disney» обнаружили, что это ощущение масс – как раз то, что отделяет хорошую анимацию от плохой. Согласно эпической книге «Disney Animation: The Illusion of Life» авторства Frank Thomas и Ollie Johnston, аниматоры компании «Disney», даже просто вешая постер в студии, должны всё время задавать себе вопрос: «Есть ли в их рисовке масса, глубина и баланс?»
Но уже сегодня почти каждая игра имеет физический двигатель, не так ли? Несомненно, именно это удерживает вашу машину от падения за край игрового мира, благодаря нему ваши персонажи не улетают в космос, когда прыгают, и это отбрасывает вашу лодку в сторону, когда рядом взрывается ракета. Тем не менее, большинство физических двигателей в современных играх довольно слабые. Они справляются лишь с задачей по удержанию машины от падения за край мира, но их возможностей недостаточно, чтобы вывести игру на новый уровень – где остов машины, потерпевшей крушение, может взорваться прямо на трассе, вызвав крен стен и других машин.
Часто игнорируемые физические возможности включают в себя практически всё: от простых эффектов вращения (вызванных удалением от центра), до появления в игре существ с искусственным интеллектом – не таких, что завязаны на статической анимации – а таких, что могут вызывать новые физические взаимодействия. Я полагаю, что многие разработчики игнорируют эти возможности, потому что они не понимают математику, описывающую физику, или были слишком заняты созданием карт текстур, чтобы выучить ее. Натиск аппаратных средств для работы с 3D позаботится о последнем, а я начинаю новый цикл статей. Первая статья позволит позаботится о формальностях. К концу нашего цикла, вы сами сможете создать физический двигатель, который вызовет у игроков ощущение полного погружения в игровой процесс, или благодаря невероятному реализму, или же – занимательному, но стойкому сюрреализму.
Предупреждение! Физика = математика, вы не можете отделить одно от другого и иметь прекрасно выполненную работу. Перед тем, как это отпугнет вас, позвольте заметить, что математика, описывающая физику, не только элегантная и прекрасная, она также имеет и прикладной характер. То есть, то не абстрактная математика для математики. Каждое уравнение, которое мы используем имеет действительный физический смысл. Мы создаем уравнения из физической модели, и взамен уравнения говорят нам, как модель ведёт себя во времени.
Грандиозное предприятие
Физика – это широкое научное поле. Мы же в действительности заинтересованы в её небольшом разделе под названием «динамика», а если точнее, «динамика твёрдых тел». Динамику можно определить в терминах родственного раздела – кинематики (учении о движении во времени). Кинематика не заостряет своё внимание на том, что вызывает движение или как тела оказались там, где они есть, она просто описывает движение. Динамика же наоборот описывает силы и массы, которые способствуют значениям из кинематики изменяться во времени. Как далеко улетит мячик для бейсбола, если время полета составит 10 секунд, а его начальная скорость 50 километров/час, а траектория – прямая линия – это проблема кинематики; как далеко улетит мячик для бейсбола в гравитационном поле земли, если я ударю по нему битой – это проблема динамики.
Часть динамики, описывающая твердые тела, имеет отношение к ограничениям, которые мы добавляем для симулируемых объектов. Форма твёрдого тела не меняется по ходу симуляции – тело скорее деревянное или металлическое, чем желеобразное. Мы можем создать сочленённые фигуры, например, человека, построив каждую часть фигуры из твёрдого тела и создав связки между ними, но мы не будем рассчитывать на гнущиеся под силовым напряжением кости или подобные эффекты. Это позволит нам упростить наши уравнения без потери качества интересного динамического поведения тел.
Даже при том, что мы рассмотрим такую небольшую часть динамики, динамика твердого тела потребует серию статей для объяснения сути. Мы начнём наше путешествие с изучения основ программирования компьютера для описания движения плоского твердого тела под действием сил. Я настойчиво повторяю «программирование компьютера, т. к. в дополнение к уравнениям, которые мы напишем для кинематики и динамики, мы также научимся, как решать эти уравнения используя вычисления с числами с плавающей точкой, что жизненно важно знать каждому программисту». Я говорю «плоское твердое тело», потому что мы будем разбираться лишь с двухмерным миром на протяжении следующей статьи и далее. Принципы – а по факту больше, чем просто уравнения – возможно переложить также и на трёхмерный мир, но определенно все гораздо проще в двумерном, поэтому мы будем учиться там, пока не почувствуем себя уверенно для выхода в трехмерное пространство. В будущих статьях мы научимся описывать эффект вращения, обработку соприкосновений тел, и, конечно, как делать всё это в трёхмерном мире. Что ж, хватит слов! Давайте начнём!
Работа с производной
Это может оказаться для вас сюрпризом, но вы в действительности не можете сдвинуть объект, просто надавив на него. Я знаю, вы думаете, что я не прав, доказывая мне обратное тем, что выбрасываете этот журнал в мусорку за то, что я написал такой вздор, но это правда! Лишь оказание давления на журнал никогда напрямую не повлияет на его позицию в пространстве. В действительности, оказание давления даже не влияет напрямую на его скорость. То, на что в действительности влияет оказание давления – так это на ускорение журнала, и фактически это одно из самых важных заключений в истории науки.
Для того, чтобы использовать этот факт с целью сделать что-нибудь интересное, нам сначала необходимо поговорить о связи позиции тела со скоростью и ускорением. В действительности все эти величины очень тесно связаны (как вы вероятно знаете): скорость – это показатель изменения координаты тела со временем, а ускорение – это показатель изменения скорости. Первичный инструмент для изучения изменений этих величин во времени – это вычисления. Если вы понимаете это, то мы идём дальше. Я полагаю, вы хорошо разбираетесь в математике. Мы будем использовать лишь простые скалярные и векторные вычисления (производные и интегралы), но не будет лишним, если вы знакомы с математикой в целом. Для справки: моя любимая книга о вычислениях – это «Calculus with Analytic Geometry by Thomas and Finney».
Координата, скорость и ускорение – это величины кинематики, которые беспокоят нас в этой статье. Расположение твердого тела в двумерном мире – это очевидно пара координат X и Y, которыми обозначаются координаты пространства какой-то заданной точки тела. Производная для вектора координат – это вектор скорости, и он показывает нам, в каком направлении движется точка (и тело, если мы игнорируем вращение, что и происходит сейчас) и как быстро она движется. Векторное исчисление – это просто скалярное исчисление каждого элемента вектора, поэтому производная от координаты X – это скорость тела по X, и так далее. Введём следующие обозначения. Пусть координата тела – это вектор r, а скорость – это вектор v или вектор r со штрихом. Получаем уравнение:
$$display$${{dx} over {dt}} = v = r'$$display$$
Уравнение 1
Если же мы продифференцируем вектор скорости по времени, это покажет, как вектор координаты изменяется со временем. Ускорение определяется по аналогии. Это первая производная от скорости или вторая производная от вектора координаты:
$$display$${{d^2 r} over {dt^2}} = r'' = {{dr'} over {dt}} = {{dv} over {dt}} = v'=a$$display$$
Уравнение 2
Интеграл от ускорения даст нам скорость, а дважды проинтегрировав ускорение, мы получим координату.
Эти взаимосвязи в кинематике показывают, что мы можем найти ускорение объекта, мы можем проинтегрировать его по времени, чтобы получить скорость и координату. Как мы дальше увидим, мы будем обращаться к интегрированию много раз в нашем коде для симуляции и будем рассчитывать новую позицию для нашего твёрдого тела для каждого кадра. Ура анимации!
Здесь представлен простой пример для одномерного мира, который мы можем аналитически проинтегрировать. Условимся, что мы хотим найти изменение координаты с конца последнего кадра по время текущего кадра для отрисовки текущей позиции. Дальше скажем, что ускорение нашего твердого тела было равно 5 условных единиц/секунду^2. Будем использовать время, прошедшее с окончания последнего кадра, как переменную t (в элементе интегрирования dt).
$$display$$v( t ) = ∫adt =∫5dt=5t + C$$display$$
Уравнение 3
Приведенные выше уравнения показывают, что скорость – это функция от времени, прошедшего с последнего кадра. Мы обнаружили константу интегрирования, C, которая равна исходной скорости в начале периода интегрирования (при t = 0).
$$display$$v( 0) = 5(0)+C$$display$$
$$display$$v_0={C}$$display$$
Уравнение 4
$$display$$v( t )=5t+ v_0{}$$display$$
Теперь проинтегрируем наше уравнение скорости, чтобы найти координату (снова не забываем о константе интегрирования):
$$display$$r( t) =∫v(t)dt=∫5t+v_0 dt= {{5}over {2} }t^2+v_0 t+r_0$$display$$
Уравнение 5
Исходя из Уравнения 5, мы можем найти текущую позицию лишь по данному ускорению, если мы знаем исходные координату и скорость (которые мы возьмём из последнего кадра) и прошедшее время. Входная переменная – время, а значение функции – текущая позиция. Мы также будем указывать время в Уравнении 4, чтобы подсчитать конечную скорость для того, чтобы мы могли использовать это в качестве исходного условия для следующего кадра.
Да прибудет с вами сила
Теперь у нас появилось осознание, что необходимо правильно задать ускорение для интегрирования уравнений кинематики, чтобы получить анимацию. Выход динамики на сцену. Помните, как я сказал, что надавливая на что-либо, вы напрямую влияете лишь на ускорение тела? Что ж, «оказание давления» – это лишь эвфемизм для словосочетания «приложить силу» – одной из двух ключевых величин в динамике – и теперь мы можем обратиться к Ньютону, чтобы узнать, как силы влияют на ускорения. Второй закон Ньютона связывает силу F с производной массы – второй величины динамики – помноженную на скорость. Произведение массы на скорость называется «импульс тела», обозначается p:
$$display$$F = p'= {{dp}over {dt}}={{d(mv)}over {dt}}= mv'=ma$$display$$
Уравнение 6
Масса – это константа для скоростей, с которыми мы сейчас работаем, это вытекает из производной в Уравнении 6, и мы получили известное уравнение F=ma (хотя я уверен, что Ньютон изначально определял силу через производную от импульса).
Если бы мы имели дело только с материальными точками, Уравнение 6 – это то, что нам нужно в динамике. Для заданной силы данной материальной точки ускорение находится делением силы на массу. Это дает нам ускорение, которое поможет решить уравнение движения из примера выше. Тем не менее, мы имеем дело с твёрдыми телами с массой, распределенной по определенной площади (объёме, когда речь идет о трёхмерном мире), поэтому нам надо еще поработать.
Для начала рассмотрим твёрдое тело, как набор точечных масс. Мы определим полный импульс, pT, для твердого тела, как сумму импульсов всех точек, которые составляют тело (я использую верхнюю индексацию, т. к. хочу яснее показать, какие количественные величины принадлежат данным точкам):
$$display$$p^T =sum_{i} {m^i v^i}$$display$$
Уравнение 7
Мы можем значительно упростить анализ динамики твёрдого тела, введя понятие центра масс (CM). Вектор, направленный к центру масс – это линейная сумма векторов, направленных изо всех точек масс твёрдого тела, поделённая на массу всего тела, M:
$$display$$r^{CM} ={sum_{i } {m^i r^i}over{M}}$$display$$
Уравнение 8
Используя определение центра масс, мы можем упростить Уравнение 7, умножив обе части Уравнения 8 на M, продифференцируя их, и затем подставив результат в Уравнение 7:
$$display$${{d(Mr^{CM})} over {dt}} = {sum_{ i} { } {{ d (m^i r^i)over dt }}} = {sum_{ i} { } { m^i v^i }} = p^T$$display$$
Уравнение 9
Правая часть Уравнения 9 – это полный импульс по определению в Уравнении 7. Теперь посмотрим на левую часть уравнения: это скорость в центре масс, помноженная на массу всего тела. Переносим правую часть влево и получаем:
$$display$$p^T = {{d(Mr^{CM})}over {dt}} = Mv^{CM} $$display$$
Уравнение 10
Из Уравнения 10 следует, что линейный импульс равен общей массе, помноженной на скорость, направленной из центра масс, поэтому нет нужды в суммировании в Уравнении 7 для того, чтобы найти импульс, если мы знаем массу тела и направление вектора скорости центра массы. Далее все конечные итоги вычислений представляют собой нахождение интегралов для всего тела, но центр масс существует и значительно упрощает нахождение полного импульса из Уравнения 10, потому мы можем не переживать – для нахождения линейного импульса мы можем рассматривать тело как материальную точку с заданными скоростью и массой.
По аналогии, полная сила – это производная полного импульса, поэтому концепция центра масс может быть использована и для упрощения уравнения силы:
$$display$$F^T = p^T = Mv'^{CM}=Ma^{CM}$$display$$
Уравнение 11
Если кратко, то из Уравнения 11 следует, что мы можем рассматривать все силы, взаимодействующие с твёрдым телом, как если бы их вектор суммы оказывал воздействие на точку центра масс, в которой содержится масса всего тела. Мы делим силу (читай гравитацию) на M для того, чтобы найти ускорение центра масс, а затем интегрируем ускорение по времени для того, чтобы получить скорость и координату тела. Т.к. мы игнорируем эффекты вращения до следующей статьи, мы уже имеем все уравнения, которые нам необходимы для описания динамики твёрдого тела. Отметим, что Уравнение 11 не содержит информации о том, куда направлены силы, приложенные к телу. Это всплывёт, когда мы будем иметь дело с линейным импульсом и центром масс, и мы просто приложим силы к CM, чтобы найти ускорение центра масс. Когда мы подсчитаем вращение тела под действием этих сил в следующей статье, мы увидим, как используется координата приложения силы.
Ода радости
На данном этапе мы можем рассмотреть другой пример аналитического интегрирования, используя Уравнение 11 для нахождения ускорения центра масс вместо произвольно выбранной величины = 5. Тем не менее, перед нами стоит серьезная проблема, т. к. аналитическое интегрирование обычно не имеет прикладного значения, потому что оно слишком сложное, поэтому мы остановится на так называемом численном интегрировании обыкновенных дифференциальных уравнений (ОДУ). Ого, теперь это звучит, как настоящая математика! Как только вы выучите это, будет самое время поднять планку. К счастью, численное интегрирование ОДУ – это не так трудно, как может показаться на первый взгляд! Для того, чтобы понять, что же это значит, перейдем от слов к делу!
Итак, дифференциальное уравнение – это такое уравнение, в котором содержатся производные зависимых величин в добавок к самой функции, независимым переменным и параметрам. Это многословно, но вот пример для изменяющейся во времени силы в одномерном мире: F = 2t, F – это зависимая величина, а t – независимая. Значение F определяется лишь самой F. Пусть уравнение силы зависит только от скорости нашего тела. Сила сопротивления воздуха увеличивается по мере увеличения скорости самолёта. Вернёмся к примеру в одномерном мире, что если F = -v означает, что сила трения приводит к замедлению нашего тела пропорционально скорости? У нас есть проблема, т. к. мы решаем уравнение следующим образом: F = ma = -v и, разделив на m, мы получим (помните, что ускорение – это производная скорости):
$$display$$a = {{dv}over {dt}} = {-vover m}$$display$$
Уравнение 12
Это дифференциальное уравнение, (уравнение скорости содержит производную скорости в Уравнении 12) называется обыкновенным дифференциальным уравнением, потому что содержит лишь обычные производные зависимых величин (в противоположность частным производным, которые составляют дифференциальные уравнения в частных производных [УЧП], о которых мы не будем говорить).
Теперь перейдем к следующей части нашей фразы: интегрирование. Как мы ранее интегрировали dv/dt для нахождения v в условиях данного уравнения?
Это покажется невероятным, но почти каждое уравнение в физике – дифференциальное, поэтому ОДУ были отлично изучены. Дифференциальные уравнения так часто можно встретить в физике, потому нередко показатель изменения количественной величины зависит от самой величины. Например, мы уже отметили, что торможение (величина изменения скорости), включая скорость сопротивления воздуха, зависит от скорости. Другие примеры из физики: охлаждение (показатель потери тепла зависит от текущей температуры) и радиоактивный распад (скорость распада зависит от того, как много присутствует радиоактивного материала).
Конечное слово в нашей фразе – численное – наше спасение. Я говорю это, потому что теория аналитического интегрирования дифференциальных уравнений, даже самых простых, огромная и довольно запутанная. Хотя, по иронии судьбы, интегрирование ОДУ численными методами компьютера – в действительности относительно просто понять. Далее я опишу простой численный интегратор, основанный на методе Эйлера, и доработаю его в следующей статье.
Почти все численные интеграторы, но никакой другой также явно, как метод Эйлера, базируются просто на старом определении вычислений через первую производную наклонной: dy/dx определяет наклон y в зависимости от x. Например, если у нас есть линейное уравнение y = 5x, то dy/dx = 5 означает, что наклон – это константа, равная 5 для любого x, и, как можно предположить, это прямая. Немного более трудный пример – это парабола y = x2. В этом случае dy/dx = 2x, а это функция, для определения новой наклонной для каждой координаты x. Я изобразил y = x2 на Рисунке 2:
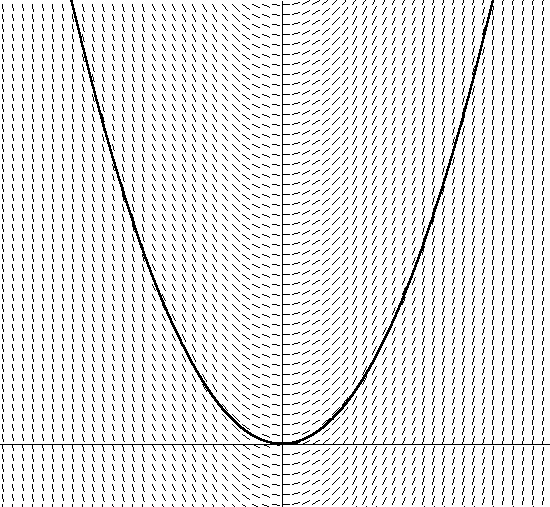
Рисунок 2. y = x2
В дополнение к этому я также изобразил штриховкой направление вектора наклонной, решив уравнение dy/dx = 2x + C для всех x. Обратите внимание на то, что угол вектора наклонной равен значению тангенса угла касательной в данной точке. Отметьте также, что существует множество различных парабол, которые удовлетворяют углу множества касательных, отличающихся лишь сдвигом по оси y. Каждая из этих парабол получается благодаря использованию различных констант интегрирования, которые содержатся в уравнении dy/dx = 2x + C. Парабола, которую я изобразил, имеет константу интегрирования, равную 0. Если я выберу другую константу, например, 1, у меня получится уравнение y = 2x + 1. Это означает, что есть аналогичная парабола со сдвигом на 1 единицу вверх по оси y.
Теперь задумайтесь о том, что если вы не знаете поле векторов на Рисунке 2, определенное параболой, то просто сядете в лужу. Итак, если вы хотите решить уравнение касательной, вам нужно просто следовать направлению вектора в каждой точке, меняя направление в соответствие с изменением направления векторного поля. Вы удивитесь от того, что по прошествии некоторого времени, вы увидите, что двигаетесь по параболической траектории (или по участку параболы), в зависимости от того, где вы начали. Сами того не осознавая, вы проинтегрировали уравнение векторного поля. Вы нашли конкретную параболу (в зависимости от того, где вы начали, или от начальных условий), используя лишь уравнение производной (просчитывая dy/dx по мере движения в векторном поле).
Проделать то же самое для реального дифференциального уравнения также просто. Для дифференциального уравнения типа dy/dx = f(x, y), нахождение производной dy/dx как касательной к f(x, y) описывает угол наклона касательной для каждой координаты на графике x, y. Если вы изображаете график векторного поля, заданного dy/dx = f (x, y), вы можете следовать этому по аналогии с параболой, путем нахождения производной в каждой точке и следовании в этом направлении. Рисунок 2 показывает векторное поле для Уравнения 12, нашего уравнения сопротивления воздуха, со скоростью по вертикальной оси и временем по горизонтальной (я произвольно выбрал m = 1 для этого графика).
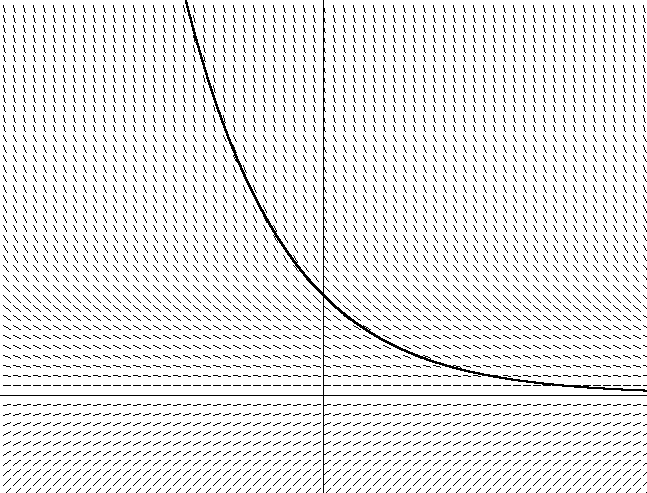
Рисунок 3. dv/dt = -v/m
Он также показывает одну из множества возможных кривых. Можно заметить, что если вы выберете начальную позицию в графике (которая зависит от начальной скорости в уравнении), по прошествии времени скорость будет стремиться к нулю, т. к. сила трения тормозит тело. Вы также можете увидеть, как уменьшение величины скорости зависит от текущего значения скорости – чем быстрее двигаетесь, тем быстрее она уменьшается. Это становится очевидно, когда из Уравнения 12 следует то же самое.
Численное интегрирование похоже на то, что мы делали на графике. Алгоритм Эйлера для численного интегрирования просто следует векторному полю в соответствие с начальной позицией через нахождение производной уравнения (-v/m для нашего примера с силой трения) для определения наклона в текущей точке, и затем просто продвигается шаг за шагом во времени, в зависимости от неизменяемой величины h, по линии наклона. Затем подсчитывается новая позиция для определения нового наклона через определенный временной промежуток:
$$display$$y_{n+1} ≈ y_{ n } + {h(dy_{ n })over dx}$$display$$
Или точнее для нашего уравнения сопротивления воздуха:
$$display$$v_{ n+1 } ≈v_{ n }+{h( -v_{n})over m}$$display$$
Очевидно, что метод Эйлера дает небольшую погрешность с каждым временным шагом, т. к. реальный вектор скорости (а поэтому и кривая решения) изгибается с отклонением в каждой точек, и алгоритм Эйлера немного отступает от угла наклона. Но если временной шаг, h – довольно малые величины, погрешность стремится к нулю. Обсудим это подробнее в будущем.
Это все, что нужно знать о численном интегрировании методом Эйлера. Вы можете спросить, как мы собираемся интегрировать скорость, чтобы получить координату. Мы просто используем снова метод Эйлера для интегрирования dr/dt = v, так же, как интегрировали dv/dt = a, по аналогии. Получим два связанных дифференциальных уравнения (еще одна наша победа):
$$display$$v_{n+1} ≈ v_n+hv'=v_n+{h F_nover M }$$display$$
$$display$$r_{ n+1 } = r_n + hr_n'= r_n+hv_n$$display$$
Это дает нам альтернативный алгоритм для вычисления координаты после действия какой-либо произвольно-приложенной силы на наш объект (что может зависеть от скорости, как мы увидели, или времени, или даже позиции нашего тела и других тела, или ото всего сразу!). Для метода Эйлера все равно, как выглядит приложенная сила, т. к. вы можете просчитать ее в любой момент времени. Эйлера интересует величина воздействия силы на массу, как наклонной, и всё.
У меня закончилось место, поэтому у меня нет возможности привести ссылки. В следующий раз я посоветую различные замечательные книги, и мы разберёмся, как просчитывать вращение твёрдых тел.
И хотя его тело не такое твердое, как хотелось бы, у Chris Hecker – динамическая личность. Если приложить силу, он ответит на e-mail checker@bix.com.
Автор: Enthusiastic_programmer





