В математике, где доказательство – это всё, важны также и факты. Однако факты хороши, только пока хороша модель, а построение моделей – занятие ненадёжное. Так какого количества фактов будет достаточно?

Можете ли вы найти следующее число в последовательности?
1, 2, 4, 8
Вот вам ещё одно число, если вам нужно больше данных для того, чтобы принять решение:
1, 2, 4, 8, 16
Следующим числом должно быть 32, не так ли? Закономерность ясна: чтобы найти следующее число, нужно удвоить предыдущее. 1 × 2 = 2; 2 × 2 = 4; 4 × 2 = 8; 8 × 2 = 16. Значит, следующее число должно быть 16 × 2 = 32. Сколько ещё фактов нужно для подтверждения этого?
Но, хотя довольно разумно предположить, что следующим числом будет 32, это не всегда будет верно. Рассмотрим следующую последовательность: будем подсчитывать количество участков, на которые разбивают круг линии, соединяющие точки, находящиеся на окружности.
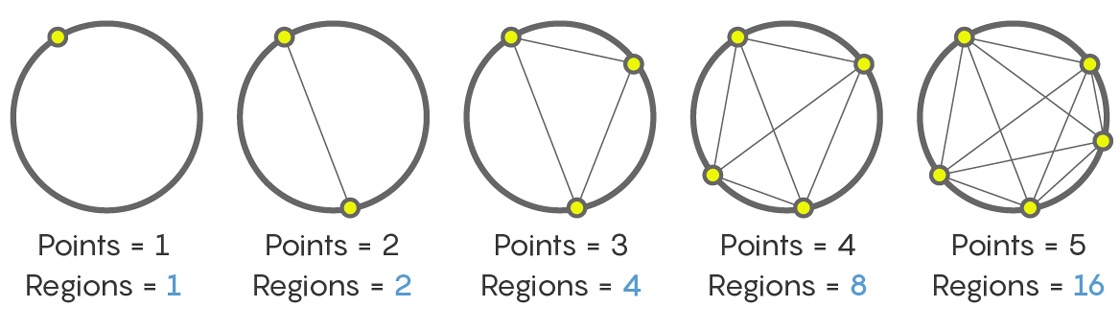
Одна точка даёт один участок (всю внутреннюю часть круга). Две точки – два участка. Три точки – четыре участка. Пять и шесть – восемь и шестнадцать, соответственно. В итоге получается последовательность
1, 2, 4, 8, 16
А сколько участков появится после соединения линиями шести точек на окружности? Никто не осудит вас, если вы, как и многие люди, впервые сталкивающиеся с этой задачей, скажете, что 32. Но это не так. На самом деле, как это ни раздражающе, ответ будет – 31! Пересчитайте сами, а потом проверьте ещё раз.
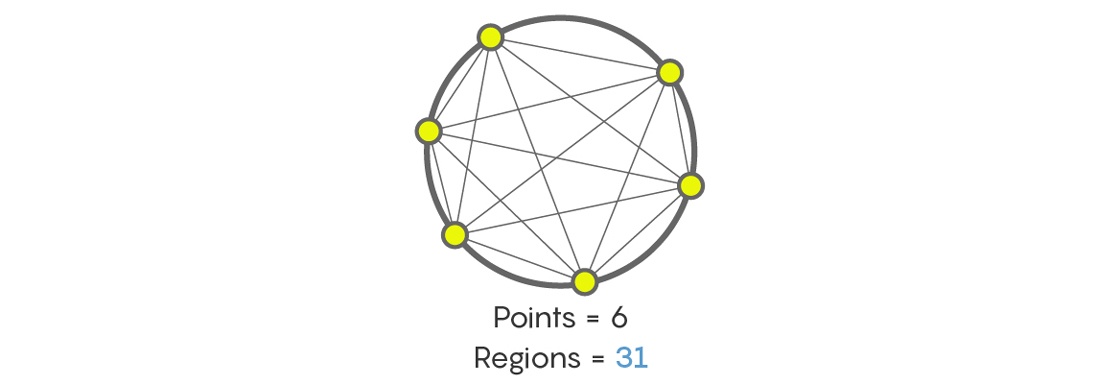
Конечно, есть последовательности типа 1, 2, 4, 8, 16, 32, 64, и так далее, из удваивающихся каждый раз чисел. Но есть и другие последовательности, например, максимальное количество участков, на которые разбивают круг линии, соединяющие точки на окружности, и это уже 1, 2, 4, 8, 16, 31, 57, 99, и так далее. Встречая последовательность 1, 2, 4, 8, 16, мы можем подумать, что все факты за то, что следующим числом будет 32, но там может быть и что-то другое.
У математики есть давняя традиция бросать вызов нашим ожиданиям и заставлять наше воображение работать. Поэтому математики всегда стремятся получить строгое доказательство, а не просто факты. Доказательство устанавливает математическую истину. Все факты могут указывать на 32 в качестве следующего числа в нашей последовательности, но без строгого доказательства мы не можем быть уверены в этом.
Но всё-таки факты для математиков полезны и важны. Часто перед тем, как доказать что-либо, мы играемся с имеющимися сведениями, изучаем задачу, рассматриваем примеры и собираем данные. Мы изучаем и взвешиваем факты и решаем, что делать дальше. Эти результаты формируют наше мнение, предлагая доказать одни теоремы и опровергнуть другие.
Гипотеза о простых числах-близнецах – это один из примеров, где факты управляют нашим математическим так же, как и доказательство. Простые числа-близнецы – это пары простых чисел, отличающихся на 2 – к примеру, 3 и 5, 11 и 13, 101 и 103. Гипотеза о простых числах-близнецах предполагает, что не существует самой большой пары таких близнецов – то есть, подобные пары постоянно появляются на числовой прямой при движении в бесконечность.
Гипотеза о простых числах-близнецах не является теоремой, поскольку, несмотря на то, что это одна из самых знаменитых задач в теории чисел, её пока никто не смог доказать. Однако почти все считают, что она верна, поскольку в её поддержку существует множество фактов.
К примеру, в своих поисках простых чисел мы постоянно находим чрезвычайно большие пары простых чисел-близнецов. В каждом из простых чисел крупнейшей из известных на сегодня пар содержится по 400 000 цифр. Также доказаны теоремы, похожие на эту гипотезу. В 2013 году Чжан Итан шокировал математическую общественность, доказав наличие бесконечно большого количества пар простых чисел, отличающихся не более, чем на 70 миллионов. Благодаря последовавшему за этим открытому проекту Polymath нам известно, что существует бесконечное количество пар простых чисел, отличающихся друг от друга не более, чем на 246. Мы до сих пор не доказали существования бесконечного количества пар простых чисел, отличающихся на 2 – но всё же 2 гораздо ближе к 246, чем 246 к бесконечности.
По этим и другим причинам вера в справедливость пусть и не доказанной гипотезы не очень спорна. Однако есть другие области математики, в которых факты используются для построения информированного мнения, оказывающегося более спорным.
В изучении эллиптических кривых её ранг, грубо говоря, обозначает численную оценку сложности решения этой кривой. Много лет считалось, что ранги эллиптических кривых не ограничены, то есть, не существует ограничений на величину ранга кривой, или на сложность решения.
Однако недавние работы заставляют математиков задуматься над возможностью ограниченности ранга. В работе даются факты, свидетельствующие о том, что возможно, существует конечное число кривых, ранг которых больше 21.
Однако стоит проявлять осторожность. Собранные математиками факты взяты не из мира эллиптических кривых – они относятся к матрицам, которые исследователи использовали для моделирования кривых. Математические модели повсеместно используются в науке, и их можно даже обратить внутрь, для изучения самой математики. Это невероятно мощные инструменты, позволяющие нам заменить непонятную нам задачу на ту, с которой нам легче справиться.
Но использование моделей – предприятие хитрое. Никогда нельзя быть уверенным, что модель ведёт себя достаточно похоже на то, что мы пытаемся понять, чтобы мы могли делать выводы из её поведения. Также нельзя быть уверенным, что наша модель похожа именно в местах, имеющих наибольшее значение. Поэтому сложно убедиться в том, что собранные нами на основе моделей факты действительно свидетельствуют о реальных свойствах изучаемых нами явлений. Давайте изучим эти проблемы на основе простой модели простой гипотезы.
Представим, что мы хотим изучить следующее заявление: любые две прямые либо пересекаются, либо параллельны.
Под пересечением будем понимать наличие у прямых общей точки, а под параллельностью тот факт, что они идут в одном направлении, но не пересекаются (это понятие можно определить и по-другому, но я буду использовать это для простоты).
Для исследования этого вопроса создадим модель. Каждую прямую представим уравнением наклонной прямой, которую вы можете помнить из школьного курса. То есть, мы предположим, что каждую прямую можно описать уравнением вида
y = mx + b
где m – наклон прямой (её крутизна), а b – точка пересечения оси y (вертикальной оси).
Моделирование прямых таким способом удобно для экспериментов над ними. Модель позволяет нам создать случайную прямую, выбрав пару случайных чисел, m и b. Мы можем выбрать пару случайных прямых и проверить их – пересекаются ли они? Идут ли в одну сторону? Происходит ли что-то ещё?
Вот несколько примеров того, как могут выглядеть результаты таких экспериментов.
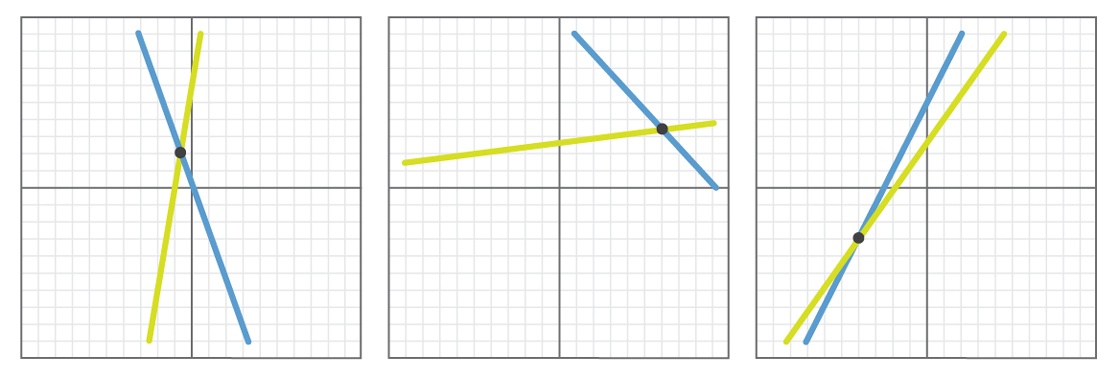
В каждом примере случайно выбранные прямые пересекаются. Если мы проведём этот эксперимент тысячу раз – или 10 000, или миллион – мы обнаружим, что во всех случаях прямые будут пересекаться или будут паралелльными (а скорее всего, все прямые будут пересекаться, поскольку маловероятно, что у двух прямых окажется одинаковый наклон, выбираемый случайно).
Поэтому, посмотрев на миллион примеров, вы можете прийти к заключению, что гипотеза, скорее всего, верна. Все факты полностью поддерживают заявление, что любая пара прямых либо параллельна, либо пересекается.
Однако факты хороши лишь настолько, насколько хороша модель, а моделирование – занятие опасное. Посмотрим, какие опасности мы создали для себя в нашем примере.
Одна проблема – определённые виды прямых будут встречаться чаще, чем другие. Вот график, где показано 50 прямых при b = 0 и 0 ≤ m ≤ 1.
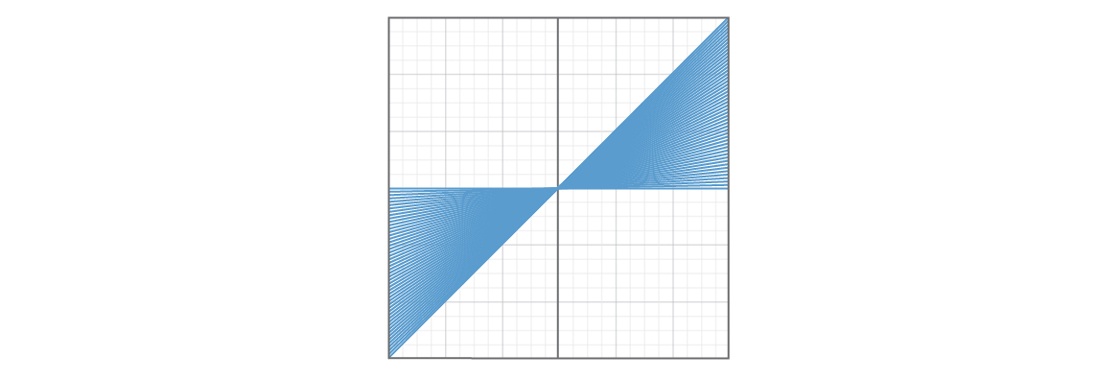
А вот график, на котором показано 50 прямых при b = 0 и m ≥ 1.
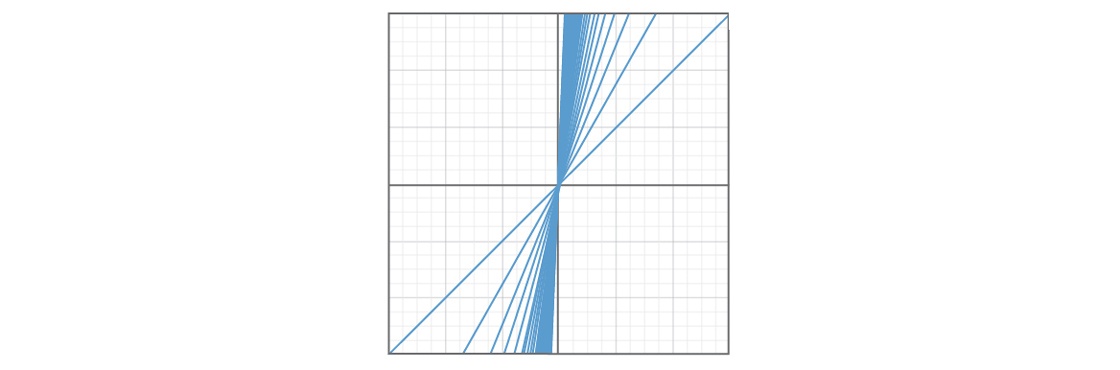
Выглядит так, будто четверть плоскости покрыта прямыми с уклоном от 0 до 1, а ещё одна четверть – прямыми с уклоном, большим 1. Выбор числа, большего 1, кажется более вероятным, чем выбор числа от 0 до 1, поэтому прямая с большей вероятностью окажется во втором участке плоскости. Это значит, что определённые прямые, с уклоном от 0 до 1, будут чрезвычайно мало представлены в модели. И если в этой части плоскости с прямыми происходят какие-то странные вещи, наша модель вряд ли расскажет нам об этом.
Если внимательно посмотреть на второй график, мы увидим ещё одну проблему. Чем больше становится m, тем круче будут прямые. Самая крутая прямая – вертикальная. Каков уклон вертикальной прямой? По определению, он не определён: нет такого числа m, которым можно было бы описать вертикальную прямую. Получается, что вертикальной прямой в нашей модели нет, и с ней мы поэкспериментировать не сможем. Мы ещё не начали сбор фактов, а уже исключили какие-то особые случаи просто из-за схемы построения модели.
Это же касается самой серьёзной проблемы нашей модели. Люди, легко представляющие себе трёхмерное пространство, вероятно, сразу заметили, что наша гипотеза неверна. Прямым не обязательно или пересекаться, или быть параллельными. Представьте себе два коридора, идущих в разных направлениях на разных этажах здания. Это скрещивающиеся прямые – прямые, которые и не пересекаются, и не параллельны.
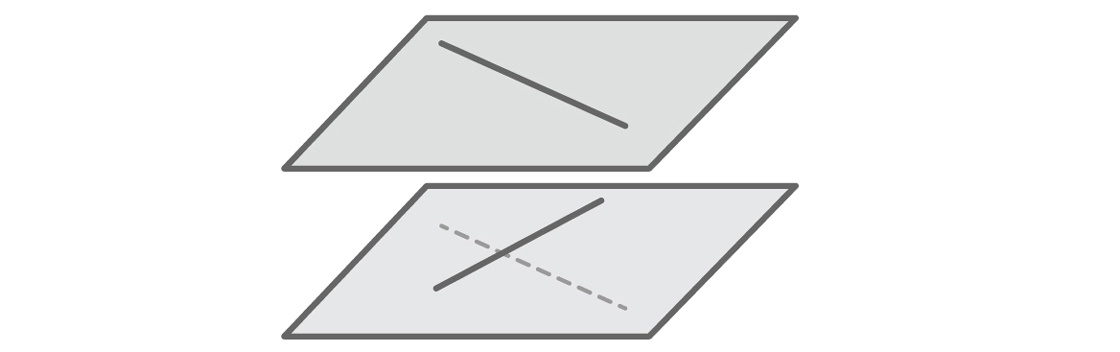
Скрещивающиеся прямые должны лежать в разных плоскостях. Но поскольку наша модель определяет любую прямую через уравнение y = mx + b, мы автоматически представили, что все прямые находятся в одной плоскости. Наша модель будет выдавать только факты, поддерживающие нашу гипотезу, поскольку если две прямые лежат в одной плоскости, они действительно должны либо пересекаться, либо идти параллельно. Других фактов мы не увидим: скрещивающихся прямых в нашей модели нет. Как и в случае вертикальных прямых, модель исключила то, что мы не смогли себе представить.
Это простой пример, использующий глупую модель с кучей проблем, включая такие каверзные вопросы, как, например, процедура выбора случайных чисел из бесконечных множеств. Профессиональные математики, изучающие ранги эллиптических кривых, никогда бы не сделали подобных упрощённых и очевидных ошибок.
Эти математики знают, какие меры предосторожности стоит принимать при работе с моделями. Им известно, что, вне зависимости от того, насколько полезна и интересна будет модель, или насколько убедительными будут собранные факты, у эллиптических кривых могут обнаружиться свойства, которые они себе не представляли. А если этого нельзя представить, ваша модель это не учтёт, и, значит, факты не отразят.
Но права новая модель, или нет, она заставила математиков продуктивно размышлять об эллиптических кривых. Если она и правда отражает истину, то идеи из мира матриц могут объяснить поведение кривых. Если нет, то понимание того, почему эллиптические кривые нельзя моделировать таким способом, может привести к лучшему пониманию задачи. Факты, собираемые нами, могут подвести нас ближе к доказательству, так или иначе.
Автор: Вячеслав Голованов



