Если Вы не читали мою первую статью на тему, советую начать с нее.
Раз уж я обмолвился про некоторое, хотя и весьма косвенное отношение к финансовым математикам, позвольте мне развить тему до абсурда исходя из того как ее развивают в Риск Аналитике. При расчете цены опциона часто считают также чувствительность этой цены к набору параметров. Например, как будет меняться цена опциона при изменении цены акции, на которую выпущен опцион, или при изменении волатильности цены акции, или ставки Центробанка и т.д.
Нас может интересовать как меняется вероятность выигрыша игры при изменении вероятности выигрыша очка. Фактически мы хотим посчитать производную от первого по второму. Простейший подход — оценить ее на глаз из графика. Видно, что максимум достигается в ситуации 50:50. При изменении шансов выигрыша очка с 0.45 до 0.55 вероятность победы в бадминтон возрастает с 0.26 до 0.74, то есть на 0.48. Грубая оценка дает производную в районе 5. То есть если с равных шансов Вы растете до 0.51 (то есть 51%), прирост в вероятности выигрыша игры будет около 0.05 (или 5%). Аналогичным образом можно посчитать производную в любой другой точке на графике.
В финансах обычно используется подход “bump and run”, то есть меняют параметр на малую величину и рассчитывают новую цену опциона и производную. Поступив аналогичным образом, привожу точные данные на графике (брал изменение на процент, слегка грубовато, но в данной ситуации приемлемо). Для большей наглядности добавил игры до 5-ти и 31 очков. Кстати, стрельба в биатлоне может рассматриваться как партия до 5. Это не абсолютная аналогия, так как общее число выстрелов фиксировано. Но методы решения практически те же.
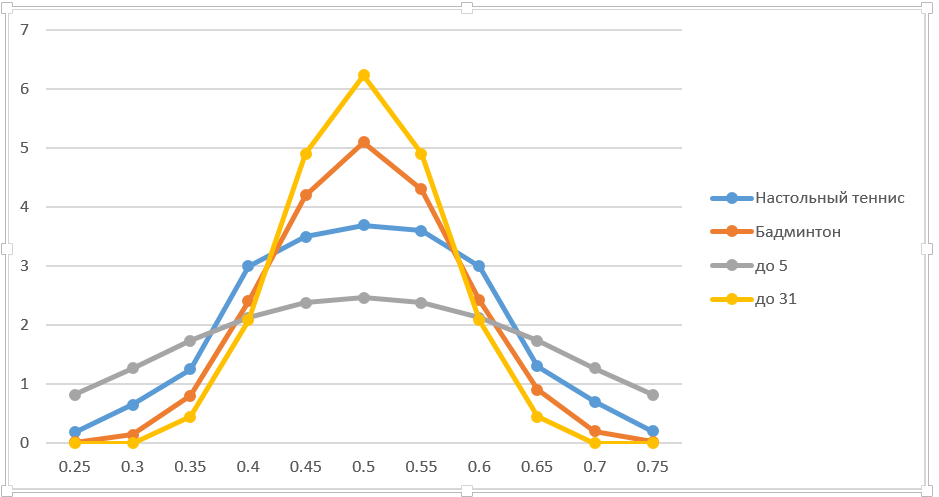
Очевидно, что чем длиннее партия, тем выше производная в точке 50:50. При стремлении длины партии к бесконечности победа игрока, имеющего даже минимальное преимущество, практически гарантирована. Ширина кривой соответственно уменьшается. В общем, выводы вполне очевидные.
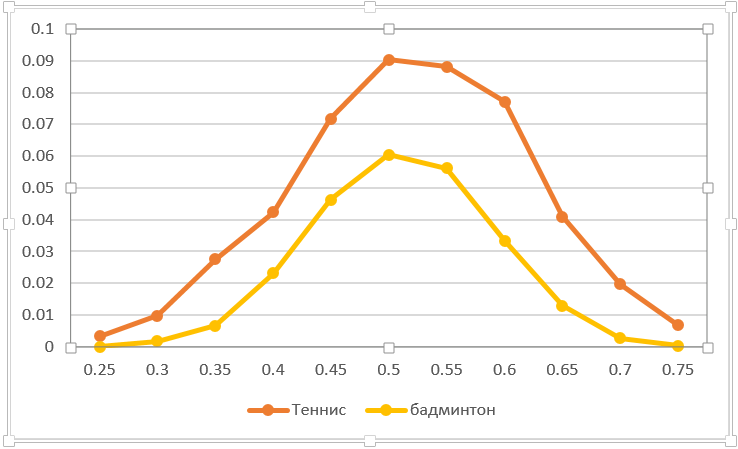
Можно рассчитать чувствительность к случайному сливу одного очка. Например, подача в сетку. Насколько один промах влияет на исход игры? Фактически это сокращение выигрышного счета для соперника на одно очко. График ниже отражает такую ситуацию. Естественно, в настольном теннисе критичнее потерять очко, чем в бадминтоне. При равных силах вероятность исхода игры падает максимально – с 0.5 до 0.41. Обратите внимание на асимметрию кривых (в отличие от большинства других). Это не случайно. Дело в том, что равновесие смещается с 50:50 в сторону большей вероятности выигрыша очка, так как потерянное очко ухудшает шансы игрока.
Давайте поставим еще один любопытный опыт. Представим, что один из игроков может сконцентрироваться и сыграть 3 очка выше среднего (p1+delta). Допустим, что после этого расклад вернется к исходному (к среднему ожидаемому без учета «прилива сил»). Ясно, что вероятность выигрыша возрастет. Вопрос в том, имеет ли значение когда именно сконцентрироваться – в начале или в конце партии? Предлагаю сделать предположение прежде чем читать дальше.
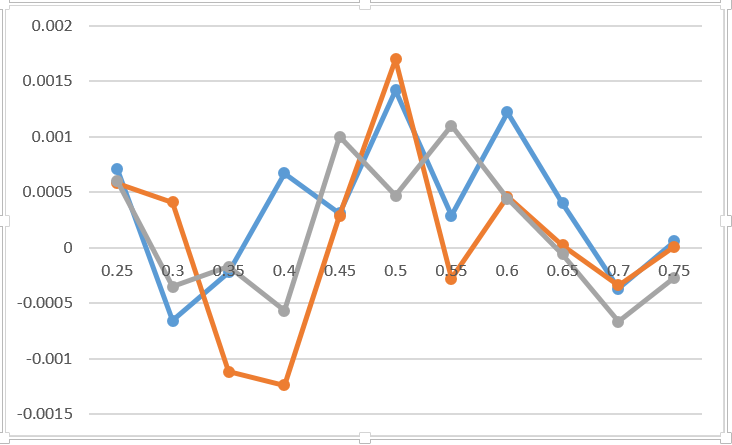
Итак, как показывает эксперимент, нет решительно никакой разницы когда именно концентрироваться (факторы морального плана не учитываются). На графике отображена разница между вероятностью выигрыша игры в случае концентрации в 3 разных местах партии по сравнению с концентрацией на первых 3-х очках. Думаю, данный график отражает погрешность Монте Карло и ничего более. Я добавлял 0.2 к исходу розыгрыша очка для первого игрока для трех розыгрышей. Я даже не указываю на графике какая линия какому варианту соответствует. Это решительно ничего не меняет. Единственный ценный совет на эту тему – соберитесь, пока не поздно.
Теперь давайте порассуждаем, что будет происходить если у одного из игроков плавает стабильность. Нервы есть нервы, ответственная игра, бывает. Допустим в среднем он набирает все тот же процент очков, но при розыгрыше конкретного очка этот процент плавает. Например, половина очков играется с вероятностью p1+delta, а другая половина – с p1-delta. При этом среднее p1 остается исходным, выпадение +delta или –delta происходит случайным образом с вероятностью 0.5. Повлияет ли это как-то на исход игры? Как показали мои эксперименты с помощью Монте Карло, разница практически не прослеживается. На самом деле, добавляя или отнимая некоторую величину, хотя и случайным образом, мы остаемся при той же средней вероятности выигрыша очка. Напрашивается предположение, что кривая распределения не влияет на исход партии, а только среднее, но я на себя такое не возьму. Тут надо думать.
Хотелось бы еще вывести дифференциальное уравнение, типа Black Scholes в финансах, чтобы завершить ассоциации. Выявить значимые производные, обнулить случайную составляющую… Еще и с дискретностью надо разбираться. Пожалуй, оставлю это настоящим финансовым математикам.
Автор: fstrlab



