Можно ли считать статистику при малом количестве данных?

в 7:11, , рубрики: Байес, Занимательные задачки, малые выборки, математика, статистика, Статистика в IT

В целом ответ – да. Особенно, когда есть мозги и знание теоремы Байеса.
Напомню, что среднее и дисперсию можно считать только, если у вас имеется определенное количества событий. В старых методичках СССР РТМ (руководящий технический материал) говорилось, что чтобы считать среднее и дисперсию необходимо 29 измерений. Сейчас в ВУЗах немного округлили и используют число 30 измерений. С чем это связано – вопрос философский. Почему я не могу просто взять и посчитать среднее, если у меня есть 5 измерений? По идее ничто не мешает, только среднее получается нестабильным. После еще одного измерения и пересчета оно может сильно измениться и полагаться на него можно начиная где-то с 30 измерений. Но и после 31го измерения оно тоже пошатнется, только уже не так заметно. Плюс добавляется проблема, что и среднее можно считать поразомну и получать разные значения. То есть из большой выборки можно выбрать первые 30 и посчитать среднее, потом выбрать другие 30 и тд … и получить много средних, которые тоже можно усреднять. Истинное среднее бывает недостижимо на практике, так как всегда имеем конечное количество измерений. В таком случае среднее является статистической величиной со своим средним и дисперсией. То есть измеряя среднее на практике мы имеем в виду «предположительное среднее», которое может быть близко к идеальному теоретическом значению.

Попробуем разобраться в вопросе, на входе мы имеем некоторое количество фактов и хотим на выходе построить представление об источнике этих фактов. Будем строить мат модель и использовать теорию Байеса для связки модели и фактов.
Можно ли считать статистику при малом количестве данных? - 1

Рассмотрим уже заезженную модель с ведром, в которое насыпали много черных и белых шаров и тщательно перемешали. Пусть черным соответствует величина 0, а белым 1. Будем их случайно вытаскивать и считать пресловутое среднее значение. По сути это и есть упрошенное измерение, так как назначены числа и поэтому и в данном случае имеется среднее значение измерений, которое зависит от соотношения разных шаров.

Вот тут натыкаемся на интересный момент. Точное соотношение шаров мы можем вычислить при большом количестве измерений. Но если количество измерений мало, то возможны спецэффекты в виде отклонения от статистики. Если в корзине 50 белых и 50 черных шаров, то возникает вопрос — есть ли вероятность вытащить 3 белых шара подряд? И ответ — конечно есть! А если в 90 белых и 10 черных, то эта вероятность повышается. И что думать о содержимом урны, если так повезло, что в самом начале совершенно нечаянно вытащили именно 3 белых шара? – у нас есть варианты.

Очевидно, что получить 3 подряд белых шара равна единице, когда у нас имеется 100% белых шаров. В других случаях эта вероятность меньше. А если все шары черные, то вероятность равна нулю. Попробуем систематизировать эти рассуждения и привести формулы. На помощь приходит метод Байеса, который позволяет ранжировать предположения и давать им числовые значения, определяющие вероятность того, что данное предположение будет соответствовать реальности. То есть перейти от вероятностного истолкования данных к вероятностному истолкованию причин.

Как именно можно численно оценить то или иное предположение? Для этого потребуется модель, в рамках которой мы будем действовать. Слава богу, она простая. Множество предположений о содержимом корзины мы можем записать в виде модели с параметром. В данном случае достаточно одного параметра. Этот параметр по сути задает непрерывный набор предположений. Главное, чтобы он полностью описывал возможные варианты. Двумя крайними вариантами являются, только белые или только черные шары. Остальные случаи где-то посередине.

Допустим, что $theta$– это доля белых шаров в корзине. Если мы переберем всю корзину и сложим все соответствующие шарам нули и единицы и поделим на общее количество, то $theta$– будет означать и еще среднее значение наших измерений. $theta in [0,1]$. (cейчас $theta$ часто используется в литературе, как набор свободных параметров, который требует оптимизации)

Самое время перейти к Байесу. Сам Томас Байес заставлял жену случайно бросать мячик, сидя к ней спиной и записывал, как его предположения соотносятся с фактами, куда он полетел на самом деле. Томас Байес пробовал на основе полученных фактов улучшить предсказания следующих бросков. Будем как Томас Байес считать и думать, а спонтанная и непредсказуемая подруга будет вынимать шарики.

Пусть $D$– это массив измерений (data). Используем стандартную запись, где знак $|$ означает вероятность выполнения события слева, если уже известно, что другое событие справа выполнилось. В нашем случае это вероятность получения данных, если известен параметр $theta$. А так же присутствует случай наоборот — вероятность иметь $theta$, если известны данные.

$P( theta | D)=frac{ P(D | theta) cdot P(theta) }{P(D)}$

Формула Байеса позволяет рассмотреть $theta$, как случайную величину, и найти наиболее вероятное значение. То есть найти наиболее вероятный коэффициент $theta$, если он неизвестен.

$theta=argmax P( theta | D )$

В правой части имеем 3 члена, которые нужно оценить. Проанализируем их.

1)Требуется знать или вычислить вероятность получения таких данных при той или иной гипотезе $P( D | theta )$. Получить три белых шара подряд можно, даже если там полно черных. Но наиболее вероятно их получить при большом количестве белых. Вероятность получить белый шар равна $P_{white}=theta$, а черный $P_{black}=(1-theta)$. Поэтому если выпало $N$ белых шаров, и $M$ черных шаров, то $P( D | theta )=theta^{N} cdot (1-theta)^{M}$. $N$ и $M$ будем считать входными параметрами наших расчетов, а $theta$ — выходной параметр.

2) Необходимо знать априорную вероятность $P(theta)$. Вот тут натыкаемся на тонкий момент моделестроения. Мы не знаем эту функцию и будем строить предположения. Если нет дополнительных знаний, то будем считать, что $theta$ равновероятно в диапазоне от 0 до 1. Если бы мы имели инсайдерскую информацию, то больше знали бы о том, какие значения более вероятны и строили бы более точный прогноз. Но так как такой информации не имеется, то положим $ theta sim равномерно[0,1] $. Так как величина $P(theta)$ не зависит от $theta$, то при вычислении $theta$ она не будет иметь значения. $P(theta)=1$

3) $P(D)$ — это вероятность иметь такой набор данных, если все величины случайны. Мы можем получить данный набор при разных $theta$ с разной вероятностью. Поэтому учитываются все возможные пути получения набора $D$. Так как на этом этапе еще неизвестно значение $theta$, то надо проинтегрировать по $P(D)=int_{0}^{1} P(D|theta) P(theta) dtheta $. Чтобы это лучше понять, надо решить элементарные задачи, в которых строится байесовский граф, а потом перейти от суммы к интегралу. Получится такое выражение wolframalpha, которое на поиск максимума $theta$ не повлияет, так как эта величина не зависит от $theta$. Результат выражается через факториал для целых значений или в общем случае через гамма функцию.

По сути вероятность той или иной гипотезы пропорциональна вероятности получения набора данных. Другими словами, — при каком раскладе мы скорее всего получим результат, тот расклад и наиболее верный.

Получаем такую формулу

$P( D | theta)=const cdot P( theta | D ) $

.

Для поиска максимума дифференцируем и приравниваем к нулю:
$0=theta^{N-1} cdot (1-theta)^{M-1} cdot (N(theta-1) + Mtheta) $.
Чтобы произведение было равно нулю надо, чтобы один из членов был равен нулю.
Нас не интересуют $theta=0$ и $theta=1$, так как в этих точках нет локального максимума, а третий множитель указывает на локальный максимум, поэтому

$theta=frac{N}{N+M}$

.

Получаем формулу, которую можно использовать для прогнозов. Если выпало $N$ белых и $M$ черных, то вероятностью $frac{N}{N+M}$ следующий будет белый. Например было 2 черных и 8 белых, то следующий белый будет с вероятностью 80%.

Желающие могу поиграться с графиком, вводя разные показатели степени:ссылка на wolframalpha.

Можно ли считать статистику при малом количестве данных? - 45
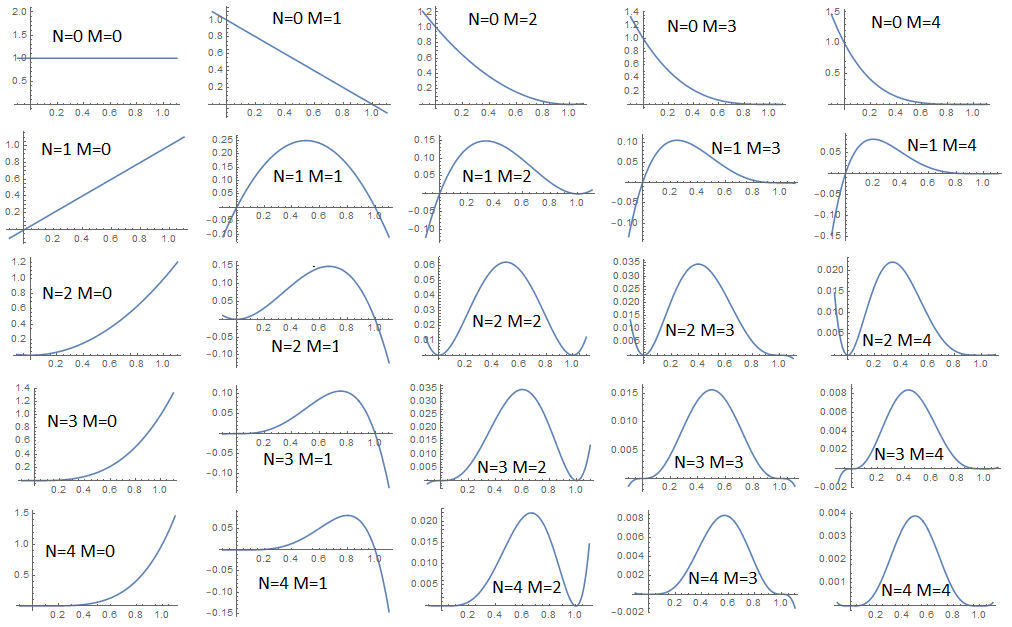
Как видно из графика, единственный случай, когда $P( D | theta )$ не имеет точечного максимума — это при отсутвии данных $N=0, M=0$. Если же мы имеем хотя бы один факт, то максимум достигается на интервале $[0,1]$ в одной единственной точке. Если $N=0$, то максимум достигается в точке 0, то есть если все шары выпали черные, то скорее всего все остальные шары тоже будут черными и наоборот. Но как уже упоминал, маловероятные комбинации тоже возможны, особенно, если купол нашего распределения пологий. Для того, чтобы оценить однозначность нашего прогноза требуется оценить дисперсию. Уже из графика видно, что при малом количестве фактов дисперсия большая и купол пологий, а при добавлении новых фактов дисперсия уменьшается и купол становится более острым.

Среднее (первый момент) по определению
$mathbb{M_{1}}=int_{0}^{1} theta cdot P(theta|D) dtheta $.

По определению дисперсия (второй центральный момент). Его то и будем считать далее в скрытом разделе.
$mathbb{M_{2}}=int_{0}^{1} (theta - mathbb{M_{1}} )^{2}P(theta|D) dtheta $.

--- раздел для пытливых умов ---

Давайте получим $P( theta | D)$ аналитически полностью, если еще не устали. Для этого приведем еще раз все члены из формулы Байеса, включая константные:
$P(theta)=1$
$P(D)=int_{0}^{1} P(D|theta) P(theta) dtheta=int_{0}^{1} theta^{N} cdot (1-theta)^{M} dtheta=frac{N!M!}{(N+M+1)!}$ ссылка на wolframalpha
$P( D | theta )=theta^{N} cdot (1-theta)^{M}$

Формула Байеса полностью для нашего случая выглядит так:

$P( theta | D )=theta^{N} cdot (1-theta)^{M} cdot frac{(N+M+1)!}{N!M!}$

Отсюда среднее после подстановки
$mathbb{M_{1}}=int_{0}^{1} theta cdot P(theta|D) dtheta=int_{0}^{1} theta cdot theta^{N} cdot (1-theta)^{M} cdot (frac{N!M!}{(N+M+1)!})dtheta=frac{(N+1)!M!}{(N+M+2)!} cdot frac{(N+M+1)!}{N!M!}$.

Используем элементраные знания $(N+1)!=(N+1) cdot N!$ и сокращая дроби

$mathbb{M_{1}}=frac{N+1}{N+M+2} $

Формула первого момента соответствует смыслу эксперимента. При преобладании белых шаров момент уходит в 1, а при преобладании черных стремится к 0. Она даже не капризничает, когда нет шаров, и довольно честно показывает 1/2.

Дисперсия выражается еще формулой, с которой будем работать.
$mathbb{M_{2}}=mathbb{M_{1}}(theta^2) - mathbb{M_{1}}(theta)^2 $.
Первый член $mathbb{M_{1}}(theta^2) $ по большей части повторяет формулу для $mathbb{M_{1}}( theta )$, используется — $theta^2$
$mathbb{M_{1}}(theta^2)=int_{0}^{1} theta^2 cdot theta^{N} cdot (1-theta)^{M} cdot (frac{(N+M+1)!}{N!M!})dtheta=frac{(N+2)!M!}{(N+M+3)!} cdot (frac{(N+M+1)!}{N!M!})$

$=frac{(N+2)(N+1)}{(N+M+3)(N+M+2)}$

,a второй уже подсчитан, поэтому
$mathbb{M_{2}}=frac{(N+2)(N+1)}{(N+M+3)(N+M+2)} - frac{N+1}{N+M+2}cdot frac{N+1}{N+M+2}$

В конечном итоге получаем:
$mathbb{M_{2}}=frac{ (M+1) cdot (N+1) }{(N+M+2)^2 cdot (N+M+3) }$
Как видно дисперсия уменьшается при добавлении данных и она симметрична относительно смены $N$ и $M$ местами.

Можно подвести итоги выкладок. При малом количестве данных надо иметь модель, параметры которой мы будем оптимизировать. Модель описывает набор предположений о реальном состоянии дел и мы выбираем наиболее подходящее предположение. Модель должна покрывать возможные варианты, которые мы встретим. При малом количестве данных модель будет выдавать большую дисперсию для выходных параметров, но по мере увеличения количества данных дисперсия будет уменьшаться и прогноз будет более однозначным.

Надо понимать, что модель, — это всего лишь модель, которая многого не учитывает. Её создает человек и вкладывает в неё ограниченные возможности. При малом количестве данных скорее сработает интуиция человека, так как человек получает намного больше сигналов из внешнего мира, и быстрее сможет сделать выводы. Такая модель скорее подойдет как элемент более сложных расчетов, так как Байес масштабируется и позволяет делать каскады из формул, которые уточняют друг друга.

На этом я бы хотел закончить свой пост. Буду рад вашим комментариям.
Можно ли считать статистику при малом количестве данных? - 70
Ссылки
Wikipedia: Теорема Байеса
Wikipedia: Дисперсия

Автор: dim2r

Источник

* - обязательные к заполнению поля

Главная   |  Архив новостей  |   Android  |   Google  |   Apple  |   Microsoft  |   Информационная безопасность  |   Веб – разработка
Публикации RSS  |  Комментарии RSS
https://ajax.googleapis.com/ajax/libs/jquery/3.4.1/jquery.min.js