Специалисты по информатике обращаются к эволюционной биологии за вдохновением для поисков оптимальных решений в наборах возможностей астрономических размеров
Изучая огромные пространства возможных решений задачи, мы сталкиваемся с тем, что большая часть путей будут тупиковыми. Но эволюция, возможно, нашла пути увеличения шансов на успех.
Креационисты обожают настаивать на том, что эволюции пришлось бы собирать до 300 аминокислот в правильном порядке, только чтобы создать единственный человеческий белок среднего размера. И поскольку на каждой позиции могла располагаться одна из 20 возможных аминокислот, казалось бы, существует более 20300 вариантов перебора, что на много порядков превышает количество атомов в обозримой Вселенной. Даже если мы обнаружим избыточность, из-за которой некоторые из этих вариантов будут эквивалентными, вероятность того, что эволюция наткнулась на правильную комбинацию случайно, проводя случайные мутации, кажется чудовищно маленькой, даже с учётом миллиардов прошедших лет.
Главным недостатком таких аргументов служит то, что эволюция не испытывала эти последовательности случайно: процесс естественного отбора отсеял ненужное. Кроме того, вероятно, что природа обнаружила и другие обходные пути, способы сузить огромное количество вероятностей до мелких, поддающихся исследованиям подмножеств, которые с большей вероятностью дадут полезные решения.
У специалистов по информатике есть сходные проблемы, которые включают в себя поиск оптимальных решений среди множеств вариантов астрономического размера. Некоторые из них обращаются за вдохновением к биологии – при том, что сами биологи лишь пытаются понять, как это получается у природы.
Генетические алгоритмы, методы оптимизации, пользующиеся популярностью уже несколько десятилетий, используют принципы естественного отбора для создания новых дизайнов (для роботов, лекарств и транспортных систем, кроме прочего), тренировки нейросетей или шифрования и расшифровки данных. Эта технология начинается с того, что случайные решения проблемы расценивают, как некие «организмы», обладающие определёнными характеристиками, или элементами, «генетически» заданными в их коде. Эти решения не особенно хороши, но затем они подвергаются различным случайным мутациям (а иногда и другим изменениям, копирующим процесс перетасовки генов) и выдают второе поколение организмов, которые в свою очередь испытывают на пригодность в решении задачи. В итоге после многих повторений этот процесс приводит к появлению чрезвычайно хорошо приспособленного индивида, или решения.
Некоторые эксперты выводят этот метод на следующий уровень, занимаясь генетическим программированием, чтобы получить программы, способные писать программы и выдавать эффективные решения (тут «генами» могут быть строки кода). Эта цель оказалась особенно сложной для достижения, поскольку исследователям приходится учитывать определённые типы данных и структуры, а также много других условий.
Что интересно, эти способы , основанные на эволюции (в особенности, генетическое программирование) концептуально пересекаются с математической теорией, всё время находившейся где-то на периферии как биологии, так и информатики. В последнее время некоторые учёные путаются использовать её, чтобы разобраться в том, как эволюция, природная и искусственная, может работать эффективно, создавать что-то новое и учиться обучаться. Главным здесь было особое понятие сложности, случайности и информации, у которого не было практических применений – до сегодняшнего дня.
Обезьяны за клавиатурами
Эта теория, придуманная в 1960-х, работает с тем, что называется алгоритмической информацией. Она отталкивается от интуитивного способа о вероятности и сложности: идеи о том, что для некоторых входных данных с вычислительной точки зрения будет проще описать, как что-то создать, чем создать это. Возьмём известную аналогию с обезьяной, жмущей на клавиши случайным образом. Шансы на то, что она напечатает первые 15 000 цифр числа π до смешного малы – и они экспоненциально уменьшаются с ростом количества цифр.
Но если интерпретировать нажатия на клавиши как случайный текст для компьютерной программы, выводящей число π, то шансы на успех, или «алгоритмическая вероятность» радикально улучшаются. Код для вывода первых 15 000 цифр числа π на языке C, к примеру, можно ужать всего до 133 символов.
Иначе говоря, алгоритмическая теория информации говорит, что вероятность выдать некоторые типы выходных данных гораздо выше, когда случайные процессы работают на уровне программы, описывающей эти данные, чем на уровне самих данных, поскольку программа будет короткой. В этом смысле, сложные структуры – например, фракталы – гораздо легче получить случайно.
Однако с таким подходом вскоре возникла проблема: математики выяснили, что алгоритмическую сложность (также известная, как Колмогоровская сложность, названная в честь Андрея Николаевича Колмогорова, одного из основателей теории) заданных выходных данных – длину кратчайшей из возможных программ, которая их выдаст – вычислить нельзя. Поэтому специалисты по информатике не могут найти идеальный способ сжатия строки или другого объекта.
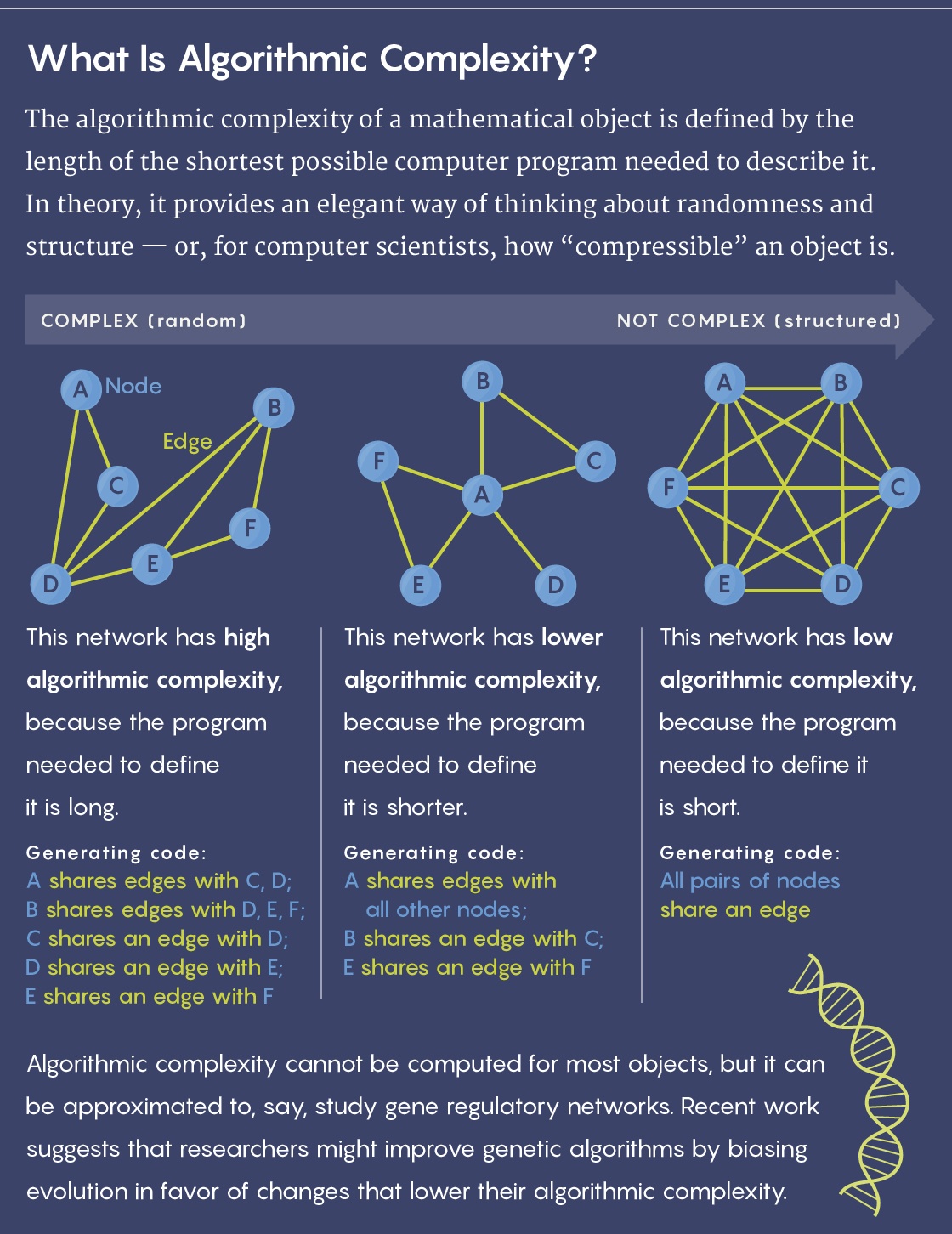
Алгоритмическая сложность сети слева высока, поскольку для её описания требуется перечислить все рёбра, соединяющие вершины. В середине сложность поменьше, поскольку при описании данной сети можно записать, что вершина A соединяется со всеми остальными. У правой сети сложность наименьшая, поскольку её описание состоит в том, что все вершины соединены рёбрами попарно.
В результате алгоритмическая теория информации разрабатывалась в основном в области чистой математики, где её используют для изучения связанных теорем и определения концепций случайности и структуры. Практическое её использование казалось недоступным. «Математически это простая и красивая мера сложности, — сказал известный математик Грегори Чайтин, один из основателей теории, работавший в Центре IBM имени Томаса Дж. Уотсона и Федеральном университете Рио-де-Жанейро. – Но с точки зрения применимости в реальном мире она выглядела неприступной».
Но это не заставило его отступиться. Он понадеялся, что эту теорию можно использовать для формализации идеи о том, что ДНК ведёт себя, как программа. В 2012 году он издал книгу, где описал, как эволюцию можно представить в качестве случайной прогулки по программному пространству. Мутации, происходящие вдоль этого пути, писал он, не подчиняются статистически случайному распределению вероятности; они подчиняются распределению, основанному на колмогоровской сложности. Но он не мог это проверить.
Теперь некоторые учёные надеются возродить эту теорию в этом контексте, и связать её одновременно и с биологией, и с информатикой.
Стремление к простоте
Гектор Зенил, специалист по информатике из Каролинского института в Швеции, один из тех, кто пытается возродить эту теорию. Он работает совместно с другими исследователями над тем, чтобы использовать колмогоровскую сложность в качестве метрики для анализа сложности биологических сетей – к примеру, генных регуляторных сетей или взаимодействия белков в клетках. Исследователи примерно оценивают алгоритмическое содержание сети (точное значение невычислимо), затем проводят мутацию сети и проверяют, насколько она повлияла на колмогоровскую сложность. Они надеются, что этот метод дасть им представление об относительной важности различных элементов сети, и о её функциональной реакции на намеренные изменения.
Известный математик Грегори Чайтин, один из основателей алгоритмической теории информации
В недавней работе, выложенной на arxiv.org, они описали, что если заставлять сеть двигаться по направлению к увеличению колмогоровской сложности – вводя мутации, из-за которых описывающая сеть программа становилась больше – то это обычно приводит к увеличению количества функций, которые способна выполнять сеть, одновременно делая её более чувствительной к возмущениям. Когда они заставляли сеть становиться проще, функций становилось меньше, а стабильность увеличивалась.
Однако пока остаётся неясным, может ли колмогоровская сложность играть какую-то большую роль, нежели простой инструмент – к примеру, как считает Чайтин, быть основной движущей силой изменений. Несмотря на все проблемы, алгоритмическая информация кажется привлекательной теорией для биологии. Традиционно для описания эволюционной динамики математику использовали в области популяционной генетики – статистических моделях, описывающих частоту появления генов в популяции. Однако у популяционной генетики есть свои ограничения: она не описывает происхождение жизни и другие основные биологические переходные процессы, или же появление совершенно новых генов. «В этой красивой математической теории как-то потерялась идея биологического творчества», — сказал Чайтин. Но если учесть алгоритмическую информацию, сказал он, «то творчество естественным образом встраивается в общую картину».
Как и идея о том что эволюционный процесс со временем улучшается и повышает эффективность. «Я убеждён, что эволюция обучается, — сказал Дэниел Полани, специалист по информатике и профессор искусственного интеллекта из Хертфордширского университета в Англии. – Я не удивлюсь, если это можно будет выразить через асимптотическое уменьшение алгоритмической сложности».
Зенил с командой решили экспериментально проверить биологические и вычислительные последствия влияния платформы алгоритмической сложности. Используя ту же технику приблизительной оценки сложности, которую они использовали для анализа и возмущения сетей, они проводили «эволюцию» искусственных генетических сетей по направлению к определённым целям – матрицам из нулей и единиц, обозначавших взаимодействия генов – делая выбор в пользу мутаций, производивших матрицы с меньшей алгоритмической сложностью. Иначе говоря, они делали отбор в пользу более крупных структур.
Гектор Зенил, специалист по информатике из Каролинского института
Недавно они опубликовали результаты в журнале Royal Society Open Science, из которых следует, что по сравнению со статистически случайными мутациями их отбор мутаций привёл к существенному ускорению развития сетей по направлению к решениям. Появились и другие особенности, например, постоянные и регулярные структуры – секции матриц, уже достигшие определённой степени простоты, которые новые поколения вряд ли бы смогли улучшить. «Отдельные регионы были более или менее подвержены мутациям просто потому, что они уже достигли определённого уровня простоты, — сказал Зенил. – Это было очень похоже на гены». Эта генетическая память помогла быстрее возникнуть крупным структурам – исследователи считают, что из этого следует, что алгоритмически вероятные мутации могут приводить ко вспышкам разнообразия и вымираниям.
«Это значит,- сказал Зенил,- что вполне плодотворно будет рассматривать вычислительные процессы при изучении эволюции». Он надеется использовать это понимание случайности и сложности, чтобы определить пути обмена, которые могут быть сильнее подвержены мутациям, или понять, почему определённые взаимодействия генов можно связать с такими болезнями, как рак.
Эволюция программ
Зенил надеется понять, работает ли биологическая эволюция по тем же вычислительным правилам, но у большинства экспертов есть сомнения. Неясно, какой естественный механизм мог бы отвечать за приблизительную оценку алгоритмической сложности или заставлять мутации развиваться целенаправленно. Более того, «считать, что жизнь полностью кодируется четырьмя буквами, будет неправильно», — сказал Джузеппе Лонго, математик из Национального центра научных исследований во Франции. «ДНК чрезвычайно важна, но не имеет смысла вне клетки, организма, экосистемы». Работают и другие взаимодействия, и применение алгоритмической информации не может охватить всю эту сложность.
И всё же эта концепция вызвала определённый интерес – в частности потому, что у таких взглядов на эволюцию и вычислительные процессы есть что-то общее, по меньшей мере, общая тема, с целью генетического программирования – получить программу, способную эволюционировать.
Уже существовали довольно интригующие намёки на потенциальную связь между идеями Чайтина и Зенила, связанными с колмогоровской сложностью и методами генетического программирования. К примеру, в 2001 году команда исследователей сообщила, что сложность выходных данных генетической программы ограничивается колмогоровской сложностью первоначальной программы.
Но по большей части колмогоровская сложность не играла роли в попытках специалистов по информатике понять эти идеи. Они пробовали другие способы изменения генетики и мутаций. Некоторые группы изменяли скорость мутаций, другие заставляли систему склоняться к мутациям, заменявшим крупные куски кода. «Люди придумали десятки, а возможно и сотни различных версий мутаций и генотипов», — сказал Ли Спектор, специалист по информатике из Хэмпширского колледжа в Массачусетсе. Спектор недавно руководил командой, продемонстрировавшей преимущества добавления и удаления мутаций по всему геному организма перед прямой заменой одного гена другим. Этот новый вид генетического оператора экспоненциально увеличивал количество путей по пространству генетического поиска и приводил в итоге к лучшим решениям.
Ли Спектор, специалист по информатике из Хэмпширского колледжа в Массачусетсе
При этом многие исследователи пошли в противоположном направлении, в поисках хитроумных способов ускорить процесс, сужая поле поисков, но не ограничивая его так сильно, чтобы поиск пропускал бы оптимальные результаты. Одна из идей состояла в том, чтобы сделать целью простоту: в 1960-х Юджин Вигнер отметил «необоснованнцю эффективность математики в естественных науках», и специалисты по информатике обнаружили, что часто более простые и элегантные модели оказываются более эффективными и чаще применимыми. «Вопрос в том, — сказал Спектор, — сообщает ли нам этот факт нечто глубокое об устройстве Вселенной, или нет? И будет ли он нам полезен?»
Он также предупреждает, что попытки подталкивать эволюционирующие программы к простоте могут оказаться деструктивными: награждение программ за краткость может привести к урезанию того, что кажется мусором сейчас, но может оказаться полезным для будущих поколений, в результате чего будут принесены в жертву оптимальные решения. «И мы застрянем», — сказал он.
Однако простота остаётся соблазнительной целью, которая, к тому же, продемонстрировала свою полезность. В опубликованной в прошлом году работе Спектор с коллегами обнаружили, что если уменьшить размер программ – иногда всего лишь на 25% от первоначальной длины – после применения техник генетического программирования, то программы лучше справлялись с новыми данными и их можно было использовать на более широком спектре общих проблем.
В частности, из-за этого он следит за работой в области алгоритмической теории информации, хотя и говорит, что ещё только предстоит увидеть её влияние на эту область исследований.
Обучаемся у жизни
Возможно, команда Зенила сделала первый шаг в деле поисков этого влияния – однако для реалистичного применения их работы им сначала необходимо проверить свой метод на других типах проблем поиска.
И всё же, «они убедительно показали необходимость ограничений на основе структуры», — сказала Лариса Албантакис, нейробиолог-теоретик из Висконсинского университета, которая также работала над ускорением генетических алгоритмов через ограничение пространства поиска. «Природа структурирована, и если взять это за отправную точку, будет глупо пытаться проверять все возможные однородные мутации». И добавила: «Все, что имеет для нас смысл, каким-то образом структурировано».
И хотя Спектор скептически относится к тому, что работа Зенила можно применить к чему-то за пределами решения конкретной задачи, которую тот изучал, «информационная теория, лежащая в основе их концепций, интригующая и потенциально весьма важная вещь, — сказал он. – Мне это кажется интересным отчасти потому, что выглядит каким-то инопланетным. Возможно, есть идеи, о которых товарищи из нашего сообщества и не подозревают». Ведь алгоритмическая информация имеет отношение к большому ассортименту идей, которые некоторые эксперты по генетическому программированию могут и не включать в свои работы, например, неограниченную природу эволюции.
«У меня есть сильное ощущение наличия в этой области чего-то важного», — сказал Спектор. Однако, добавил он, пока что «между их работой и практическими применениями существует огромная дистанция».
«Идея о том, чтобы представлять себе жизнь в виде эволюционирующей программы, весьма плодотворна», — сказал Чайтин, хотя её ценность пока ещё рано определять. Рассуждаем ли мы об искусственной, или о биологической жизни, «надо посмотреть, насколько далеко мы сможем зайти».
Автор: SLY_G
