“Хьюстон, у нас проблемы”, — устало раздалось в , пытающемся в ночи продраться сквозь Datasheet IMU MPU-9250 от InvenSense. Когда все слова в отдельности понятны, но взаимосвязь их запутана до невозможности. Началось всё с параметра LSB, про который я только смутно помнила, что в переводе это Least Significant Bit. Дальше пошли “Resolution”, “Sensitivity”, а ещё дальше я поняла, что получающийся текст уже можно озаглавить “Datasheet для чайников”.
Немного об основных блоках инерционного модуля.
MEMS-гироскоп
MPU-9250 состоит из трёх независимых одноосных вибрационных датчиков угловой скорости (MEMS гироскопов), которые реагируют на вращение вокруг X-, Y-, Z- осей. Две подвешенные массы совершают колебания по противоположным осям. С появлением угловой скорости эффект Кориолиса вызывает изменение направления вибрации ($inline$vec{F}_K = -2m[vec{omega} times vec{v}_r]$inline$, которое фиксируется емкостным датчиком. Измеряемая дифференциальная емкостная составляющая пропорциональна углу перемещения [Время Электроники]. Получившийся сигнал усиливается, демодулируется и фильтруется, давая в итоге напряжение, пропорциональное угловой скорости вращения. Данный сигнал оцифровывается с помощью встроенного в плату 16-битного АЦП. Скорость оцифровки (sample rate) может программно варьироваться от 3.9 до 8000 выборок в секунду (samples per second, SPS), а задаваемые пользователем фильтры низких частот (LPF) предоставляют широкий диапазон возможных частот среза. ФНЧ нужен, в том числе, чтобы убирать вибрации от моторов (как правило, выше 20-25 Гц).
Трёхосевой MEMS-акселерометр
Использует для каждой оси отдельную пробную массу, которая смещается при возникновении ускорения вдоль данной оси (фиксируются емкостными датчиками). Архитектура MPU-9250 снижает подверженность температурному дрейфу и вариациям электропараметров. При расположении устройства на плоской поверхности оно измерит 0g по X- и Y-осям и +1g по Z-оси. Масштабный коэффициент (scale factor — отношение изменения выходного сигнала к изменению выходного измеряемого сигнала) калибруется на заводе и не зависит от напряжения питания. Каждый сенсор снабжен индивидуальным сигма-дельта АЦП (состоит из модулятора и цифрового фильтра низких частот, подробнее про устройство в [Easyelectronics]), выходной цифровой сигнал которого имеет настраиваемый диапазон измерений.
И сразу про трёхосевой MEMS-магнетометр
Основан на высокоточной технологии эффекта Холла. Включает в себя магнитные сенсоры, определяющие напряжённость магнитного поля земли по осям, схему управления, цепь усиления сигнала и вычислительную схему для обработки сигналов с каждого датчика. Каждый АЦП имеет разрешение 16 бит, диапазон измерений $inline$pm 4800mu T$inline$. Для измерения слабых магнитных полей применяют либо единицу в системе СИ микротесла (мкТл), либо гаусс (Гс, система СГС): $inline$1 Гс = 100 mu Тл$inline$, [Радиолоцман]).
Итак, что такое LSB?
- Минимальный уровень напряжения, который сможет разобрать и осознанно конвертировать АЦП.
- Mинимальное приращение напряжения на выходе ЦАП.
Как этот LSB посчитать? Инструкция по добыче
Допустим, наш акселерометр сейчас работает в диапазоне измерений $inline$FS = pm 2g$inline$, то есть полный размах возможных значений будет $inline$2 cdot FS = 4g$inline$. Соответствующие им значения напряжений оцифровываются 16-битным АЦП, который может разбить весь интервал максимально на $inline$2^{16} = 65536$inline$ ступеней. Минимальный инкремент, который можно засечь, — это как раз одна ступенька $inline$LSB = 2 cdot FS/65536$inline$. Тут надо помнить, что счёт ведётся с нуля, так что на самом деле максимально измеряемое значение будет $inline$2 cdot FS_{true} = (2^{16} - 1) * LSB = 65535 * LSB = 2 cdot FS - LSB$inline$. То есть, чем больше бит в цифровом слове АЦП или ЦАП, тем меньше будет расхождение. При этом чувствительность (иногда называется масштабным коэффициентом, sensitivity scale factor) датчика на конкретном диапазоне будет определяться как соотношение электрического выходного сигнала и механического воздействия. Традиционно указывается для частоты сигнала 100 Гц и температуры $inline$T=+25^{circ}C.$inline$ Для MPU-9250 чувствительность составляет $inline$2^{16}/(2cdot FS)$inline$ ступеней на каждые g или $inline$^{circ}/s$inline$ ($inline$LSB/g$inline$, $inline$LSB/(^{circ}/s)$inline$), для другого IMU, BMI088 от Bosch Sensortec, чувствительность гироскопа высчитывается так же, а для акселерометра используется $inline$(2^{16}-2^4)/(2cdot FS)$inline$ ступеней на каждое g.
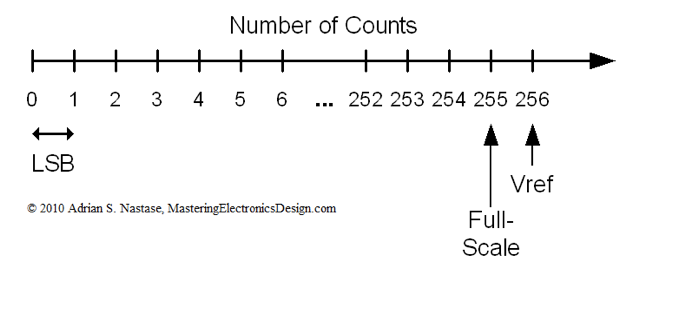
Варианты FS вытаскиваем из спецификации на гироскопы и, чтобы дважды не вставать, акселерометры.
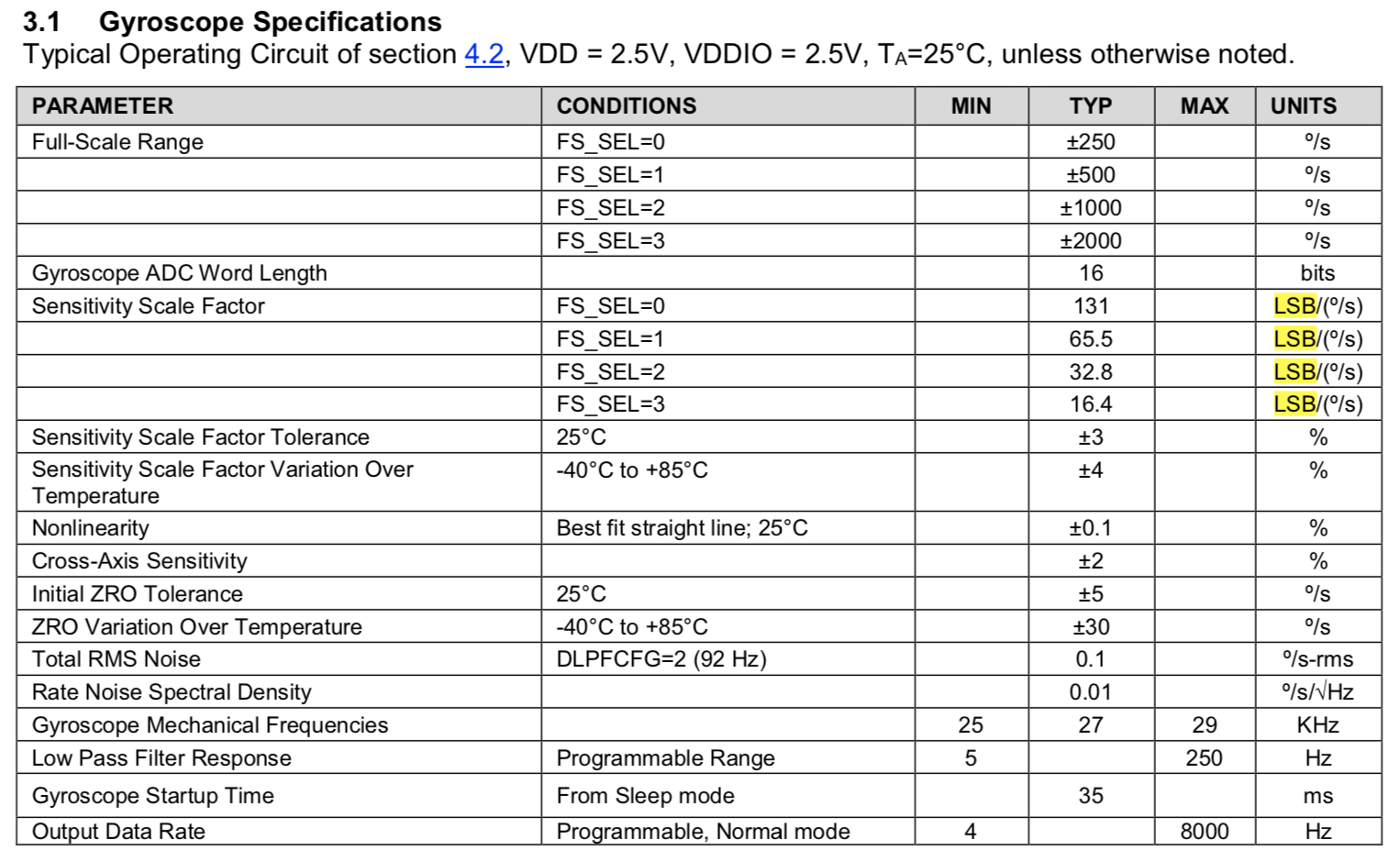
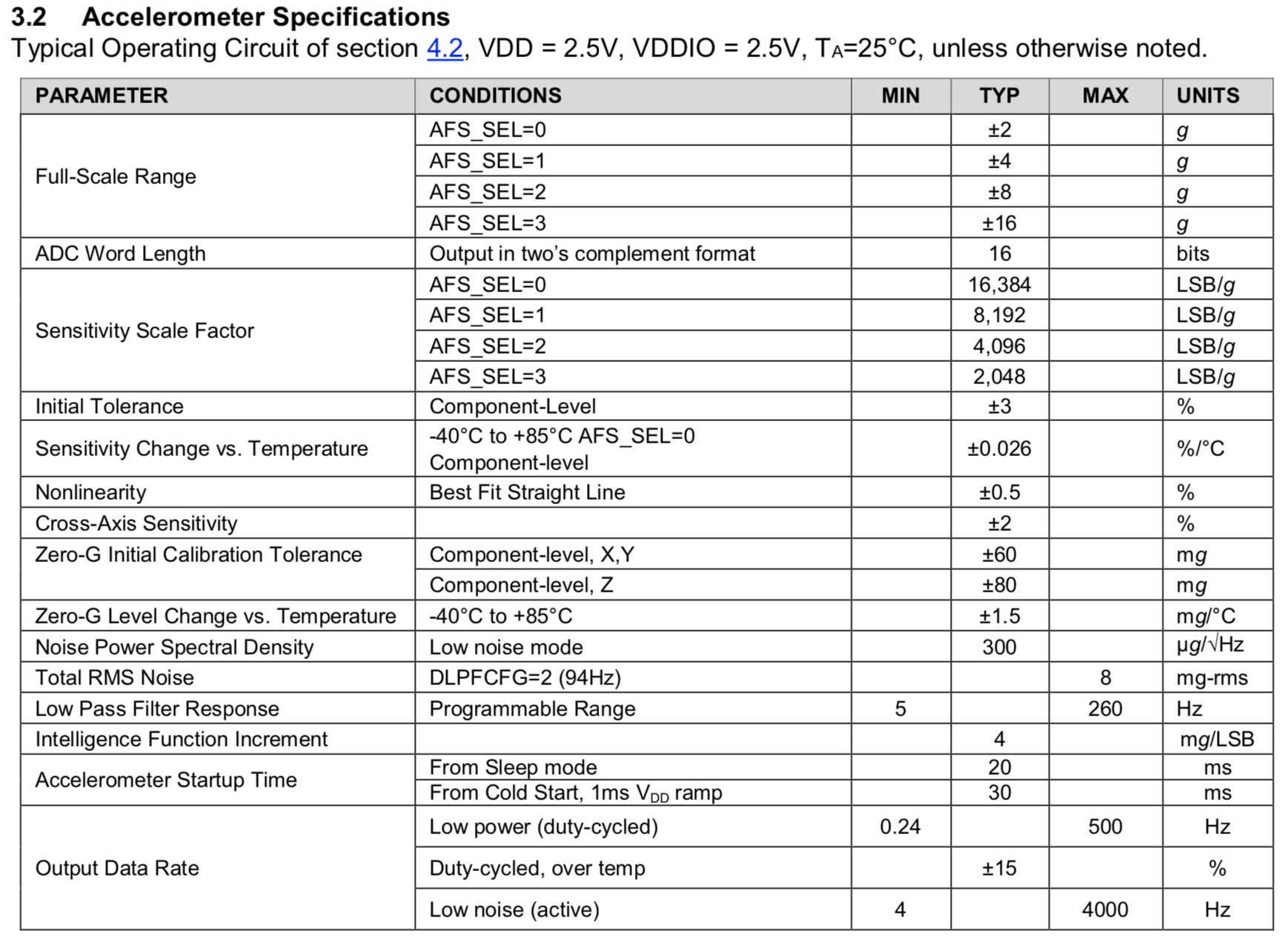
FS для акселерометров я брала ещё и из документации на BMI088 (см. ниже).
| Гироскоп, 16 бит $inline$(2^N = 65535)$inline$ | Акселерометр, 16 бит $inline$(2^N = 65535)$inline$ | ||
|---|---|---|---|
| Диапазон (FS), $inline$^{circ}/s$inline$ (dps) | LSB, $inline$^{circ}/s$inline$ (dps) | Диапазон (FS), g | LSB, mg |
| $inline$pm 125$inline$ (FS = 250) | 0,004 | $inline$pm 2$inline$ (FS = 4) | 0,06 |
| $inline$pm 250$inline$ (FS = 500) | 0,008 | $inline$pm 3$inline$ (FS = 6) | 0,09 |
| $inline$pm 500$inline$ (FS = 1000) | 0,0015 | $inline$pm 4$inline$ (FS = 8) | 0,12 |
| $inline$pm 1000$inline$ (FS = 2000) | 0,03 | $inline$pm 6$inline$ (FS = 12) | 0,18 |
| $inline$pm 2000$inline$ (FS = 4000) | 0,06 | $inline$pm 8$inline$ (FS = 16) | 0,24 |
| $inline$pm 12$inline$ (FS = 24) | 0,37 | ||
| $inline$pm 16$inline$ (FS = 32) | 0,48 | ||
| $inline$pm 24$inline$ (FS = 48) | 0,73 | ||
Всё, вроде бы, встало на свои места, можно идти дальше. В некоторых случаях (ниже, например, вырезка из документации на BMI088) отдельно указывается такой параметр, как разрешение (Resolution).
По факту, вроде бы, получается, что это должен быть LSB. Но почему тогда мы видим одно значение вместо нескольких, завязанных на конкретные диапазоны? Пришлось расширять список исследуемых источников в поисках ответов.
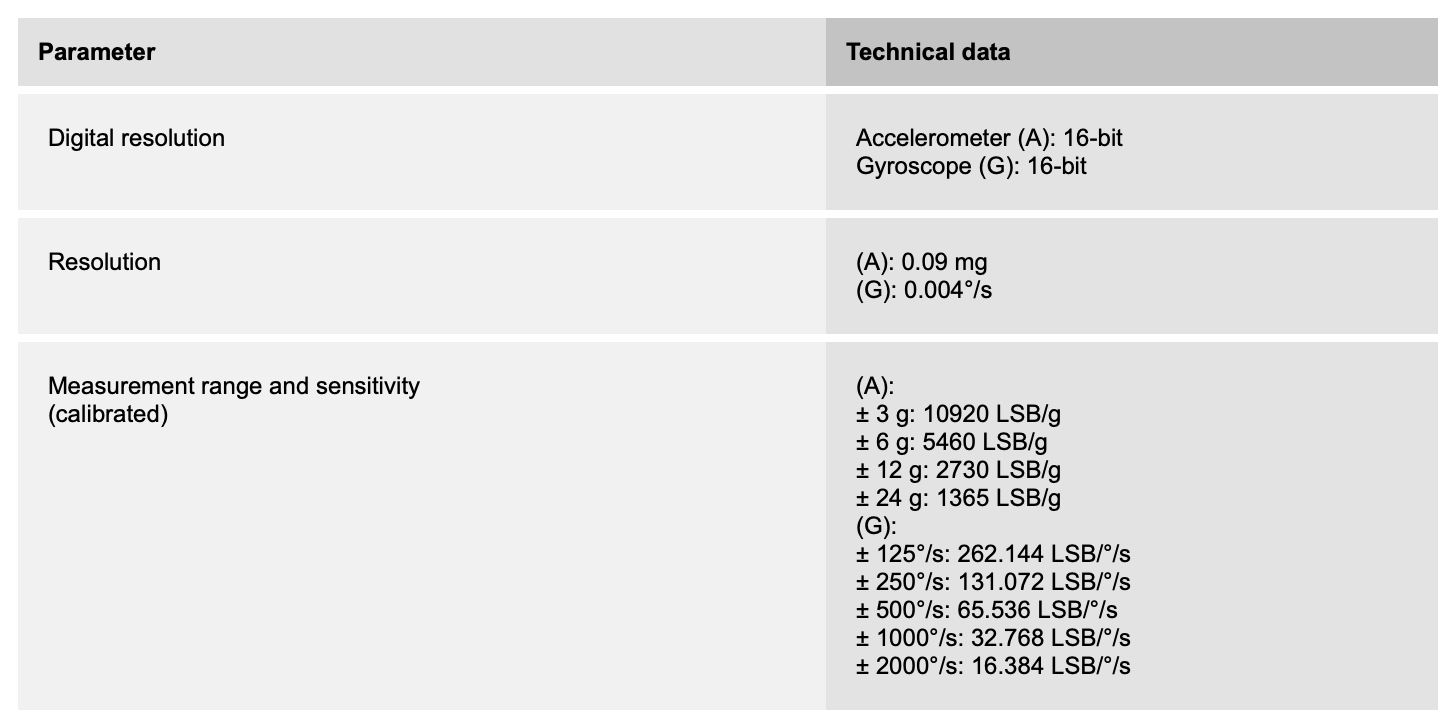
Что такое разрешение (Resolution)?
Минимальная величина, которую достоверно видит датчик, крайне важная при попытке соблюсти баланс между ценой и производительностью. Это не точность — сенсор с высоким разрешением может быть не особо точным, равно как и сенсор с малым разрешением в определённых областях может обладать достаточной точностью. К сожалению, LSB определяет лишь теоретическое минимально-различимое значение при условии, что мы можем использовать все 16 бит АЦП. Это разрешение в цифровом мире. В аналоговом какая-то часть ступеней будет зашумлена и число эффективных бит будет меньше.
Какие бывают характеристики шума и откуда что берётся?
Источники шума можно в общем разбить на электронный шум схемы, преобразующей движение в сигнал напряжения (джонсоновский тепловой шум, дробовой шум, розовый 1/f фликкер-шум и т.д.), и тепловой механический (броуновский, обусловленный наличием мелких подвижных частей) от самого сенсора. Характеристики последнего будут зависеть от резонансной частоты механической части системы $inline$f_0$inline$ (собственной частоты колебаний сенсора $inline$omega_0 = 2pi / f_0$inline$).
Среднеквадратичное значение шумов во всём спектральном диапазоне — Total RMS (Root mean square) Noise
Уровни шума можно определять несколькими способами. Можно рассматривать их во временной или частотной области (после преобразования Фурье). В первом случае берут остаточный шум как среднеквадратичное значение сигналов от неподвижного датчика (по факту это стандартное отклонение для выборки при $inline$ overline x = 0$inline$) за некоторый промежуток времени:
$$display$$x_{RMS} = sigma_X = sqrt{sum_{i=1}^n {(x_i - overline x)}^2 over{n-1} }$$display$$
Ускорения или угловые скорости вращения меньше уровня широкополосного шума будут неразличимы — вот и фактическое разрешение. Среднеквадратичное значение переменного напряжения или тока (часто называется действующим или эффективным) равно величине постоянного сигнала, действие которого произведёт такую же работу в активной (резистивной) нагрузке за время периода. Наиболее эффективен такой подход при оценке широкополосного шума, где доминирует белый шум.
Для белого шума отношение амплитуды (мгновенного пикового значения) к среднеквадратчному с вероятностью 99.9% составляет $inline$N_{PP}/N_{RMS} = 6.6.$inline$ Называется такое отношение крест-фактором (crest factor, cross ratio). Можно выбрать вероятность 95.5% — крест фактор будет равен 4.
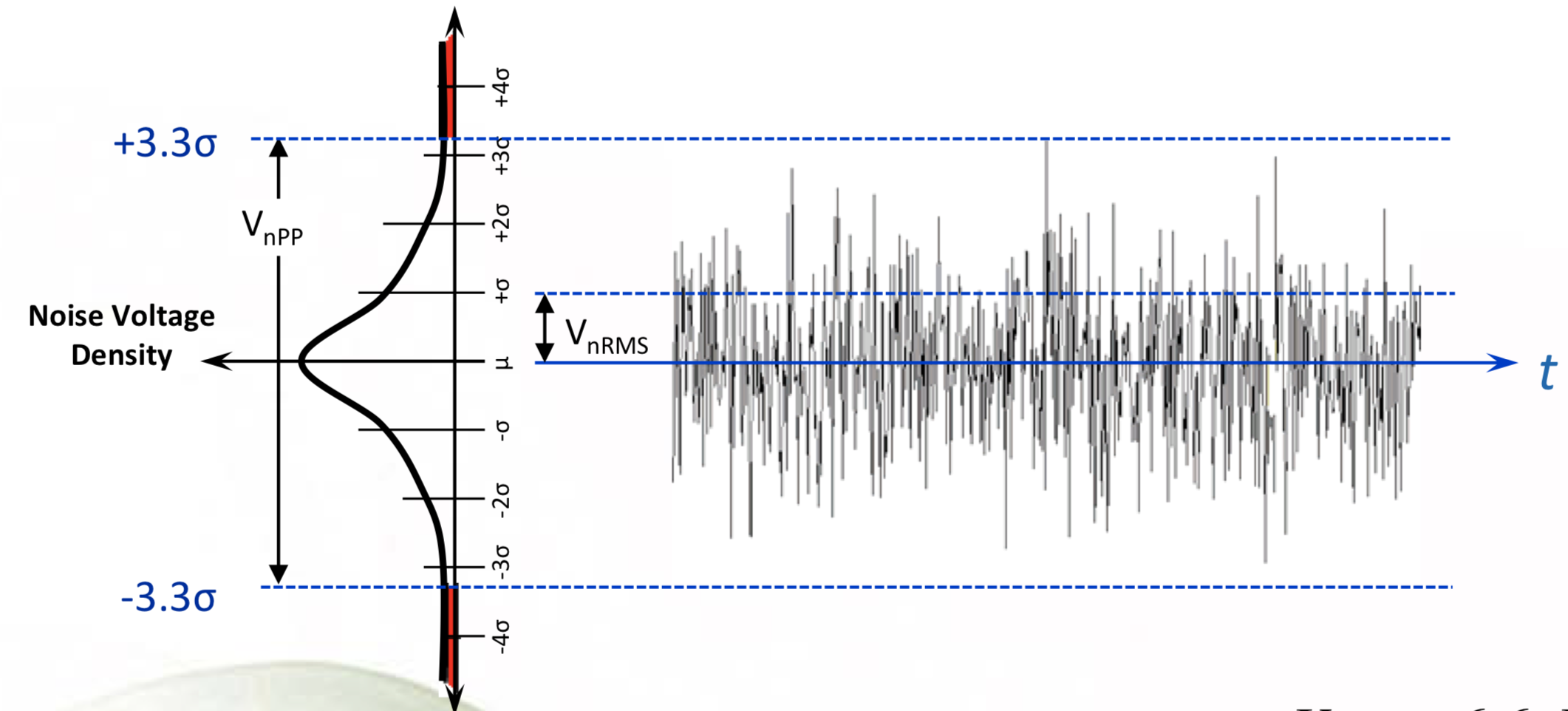
На деле же сигналы шума ведут себя не так хорошо и могут выдавать пики, увеличивающие крест-фактор до 10 раз. В некоторых спецификациях можно найти значения $inline$N_{PP}$inline$ или сам множитель.
В узкой низкочастотной полосе 0.1-10 Гц основную роль играет фликкер-шум “1/f”, для оценки которого используют значение размаха шумового сигнала (peak-to-peak).
Спектральная плотность
Иногда сигнал удобнее рассматривать в частотной области, где его описание называется спектром (зависимость амплитуды и фазы от частоты). Одна из возможных характеристик шума в спецификациях зовётся power spectral density of noise (PSD), noise spectral density, noise power density, или попросту noise density). Описывает распределение мощности шума по диапазону частот. Вне зависимости от представления электрического сигнала через ток или напряжение мгновенную рассеиваемую на нагрузке мощность можно нормировать (R = 1 Ом) и выразить её как $inline$p(t)={nu}^2(t)/R = i^2(t)R=x^2(t).$inline$ Средняя мощность, рассеиваемая сигналом в течение промежутка времени $inline$(-T/2, T/2),$inline$
$$display$$P_x^T=frac{1}{T} int^{T/2}_{-T/2}x^2(t),dt.$$display$$
Мощность – скорость поступления энергии. Через энергию определяются детерминированные и непериодические сигналы. Периодические и случайные сигналы выражаются через мощность, поскольку они не ограничены по времени и, соответственно, энергии, при этом в любой момент времени их средняя мощность отлична от нуля
$$display$$P_x = lim_{T to infty} frac{1}{T} int^{T/2}_{-T/2} x^2(t),dt.$$display$$
Можно вспомнить [Sklyar], что произвольный периодический сигнал выражается через комбинацию бесконечного числа гармоник с возрастающими частотами:
$$display$$x(lambda ) = frac{a_0}{2} + sum_{n=1}^{infty} (a_n cos n lambda + b_n sin n lambda),$$display$$
что после представления косинуса и синуса в экспоненциальной форме
$$display$$coslambda = frac{e^{i lambda} + e^{-i lambda}}{2}, sin lambda =frac{e^{i lambda} - e^{-i lambda}}{2i}$$display$$
и замены $inline$lambda = omega t=2pi f_0 t = frac{2pi t}{T_0}$inline$ можно записать в виде
$$display$$x(t) = frac{a_0}{2} + frac{1}{2} sum_{n=1}^{infty}[(a_n - ib_n) e^{in omega t} + (a_n + ib_n) e^{-in omega t}] = sum_{n=- infty}^{infty} c_n e^{in omega t},$$display$$
где комплексные коэффициенты (спектральные компоненты) ряда Фурье для $inline$x(t)$inline$,
$$display$$begin{equation} c_n = frac{1}{T_0}int^{T_0/2}_{-T_0/2} x(t)e^{-i nomega t},dt = begin{cases} frac{1}{2}(a_n-ib_n), & n>0\ frac{a_0}{2}, & n=0\ frac{1}{2}(a_n + ib_n), & n<0 end{cases} end{equation}$$display$$
В общем случае эти коэффициенты представимы следующим образом:
$$display$$c_n=|c_n|e^{i theta_n},$$display$$
$$display$$|c_n|=frac{1}{2}sqrt{a_n^2 + b_n^2}, theta_n=arctan left( frac{b_n}{a_n}right), b_0=0, c_0=frac{a_0}{2}.$$display$$
Амплитудным и фазовым спектром называют графики зависимости $inline$|c_n|$inline$ и $inline$theta_n$inline$ от частоты. Спектральная плотность мощности $inline$PSD(f)$inline$ периодического сигнала $inline$x(t)$inline$ даёт распределение мощности сигнала по диапазону частот:
$$display$$PSD(f) = sum^{infty}_{n=-infty}|c_n|^2 delta (f-nf_0)$$display$$
и имеет размерность $inline$[Вт/Гц] = [x^2/Гц].$inline$ Средняя нормированная мощность действительного сигнала будет
$$display$$P_x = int^{infty}_{-infty}PSD(f),df.$$display$$
Непериодические случайные сигналы (в частности, шум) можно описать как периодические в предельном смысле. Если $inline$T_0$inline$ стремится к бесконечности, последовательность импульсов превращается в отдельный импульс $inline$x(t)$inline$, число спектральных линий стремится к бесконечности, график спектра превращается в гладкий спектр частот $inline$X(f).$inline$ Для данного предельного случая можно определить пару интегральных преобразований Фурье
$$display$$X(f)=int^{infty}_{-infty}x(t)e^{-i 2pi f t},dt$$display$$
и
$$display$$x(t) = int^{infty}_{-infty}X(f)e^{i 2pi f t},df,$$display$$
где $inline$X(f)$inline$ — Фурье-образ.
Спектральная плотность мощности случайного сигнала определяется через предел
$$display$$PSD(f)= lim_{T to infty} frac{1}{T}|X_T(f)|^2.$$display$$
и описывает распределение мощности сигнала в диапазоне частот.
Поскольку мы предполагаем, что среднее для белого шума датчиков в неподвижном состоянии равно нулю ($inline$overline x = overline x^2 = 0$inline$), то квадрат среднеквадратического значения равен дисперсии и представляет собой полную мощность в нормированной нагрузке:
$$display$$Noise_{RMS}^2 = sigma_x^2 = P_x = int^{infty}_0 PSD(f),df = int^{Bandwidth}_0 PSD(f),df = PSD(Badnwidth - 0)$$display$$
$$display$$Noise RMS = sqrt{Noise Density times Bandwidth}$$display$$
Смотрим в спецификации — там на самом деле под именем спектральной плотности указан квадратный корень из неё с соответствующей размерностью $inline$[^{circ}/s/sqrt{Hz}]$inline$ или $inline$[mu g/sqrt{Hz}].$inline$ То есть значение RMS шума без указания полосы частот, на которой он считался (Bandwidth), бессмысленно.
Чуть подробнее про выбор полосы пропускания
На выходе MEMS-датчика мы получаем сигналы разной частоты. Предполагается, что мы заранее имеем некое представление об измеряемых нами процессах. К примеру, при определении вектора ускорения дрона шумом являются вибрации аппарата. Отделить их от полезного сигнала можно с помощью фильтра низких частот, который обрежет все частоты выше указанной (к примеру, 200 Гц). MPU-9250 предоставляет возможность настроить частоту среза фильтра низких частот с помощью параметра с магическим названием DLPFCFG. Расшифровывается он как Digital Low Pass Filter Configuration. Далее в спецификации там и тут всплывали не менее загадочные выражения типа (DLPFCFG = 2, 92Hz), но за расшифровкой пришлось лезть в другой документ, “Register Map and Descriptions”. Там показано, какие наборы битов в какие регистры надо записать для достижения желаемых эффектов:
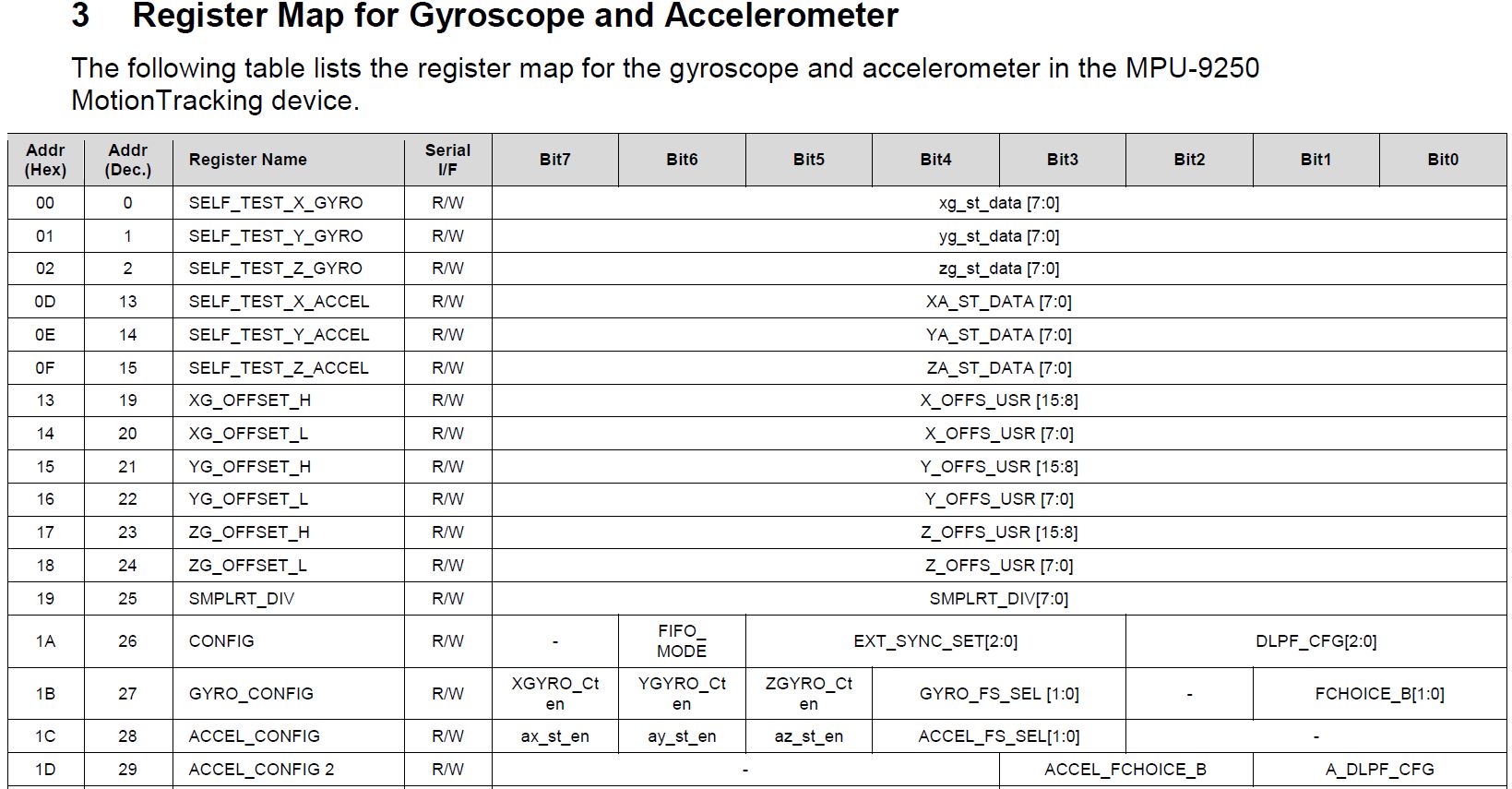
Опуская технические подробности конфигурирования, можно сказать следующее. В данном датчике осуществляется настраиваемая фильтрация показаний не только акселерометров, гироскопов, но и температурного датчика. Для каждого существует в общей сложности от 7 до 10 режимов, характеризующихся такими понятиями, как полоса пропускания (Bandwidth) в Гц, задержка в мс, частота дискретизации (sampling frequency, Fs) в кГц.
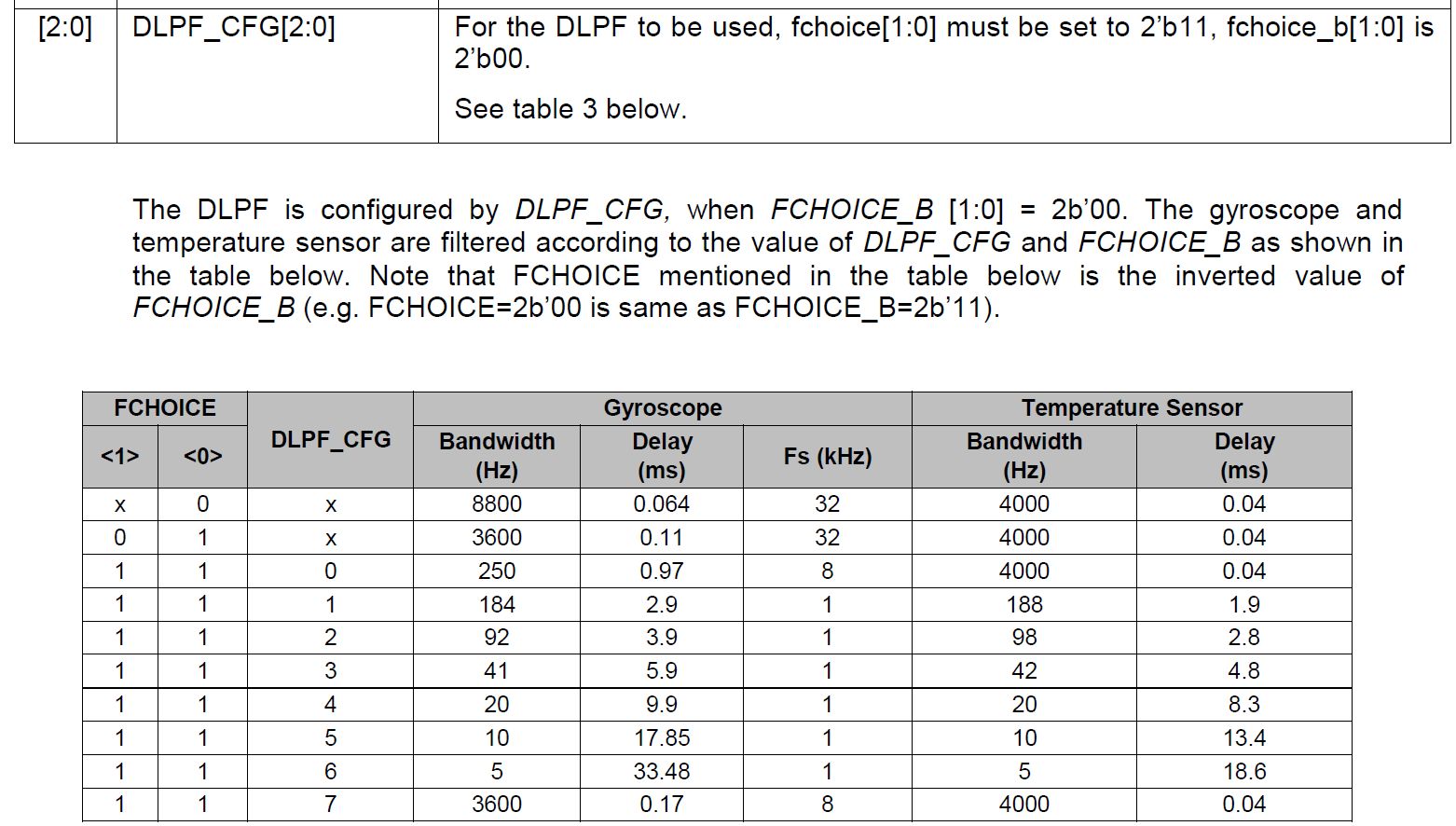
В таблицу режимов фильтра акселерометра добавилась колонка «Плотность шума» в $inline$mu g/rtHz = mu g/ sqrt{Hz}$inline$, а “Bandwidth” колонка дополнилась значением “3dB”.
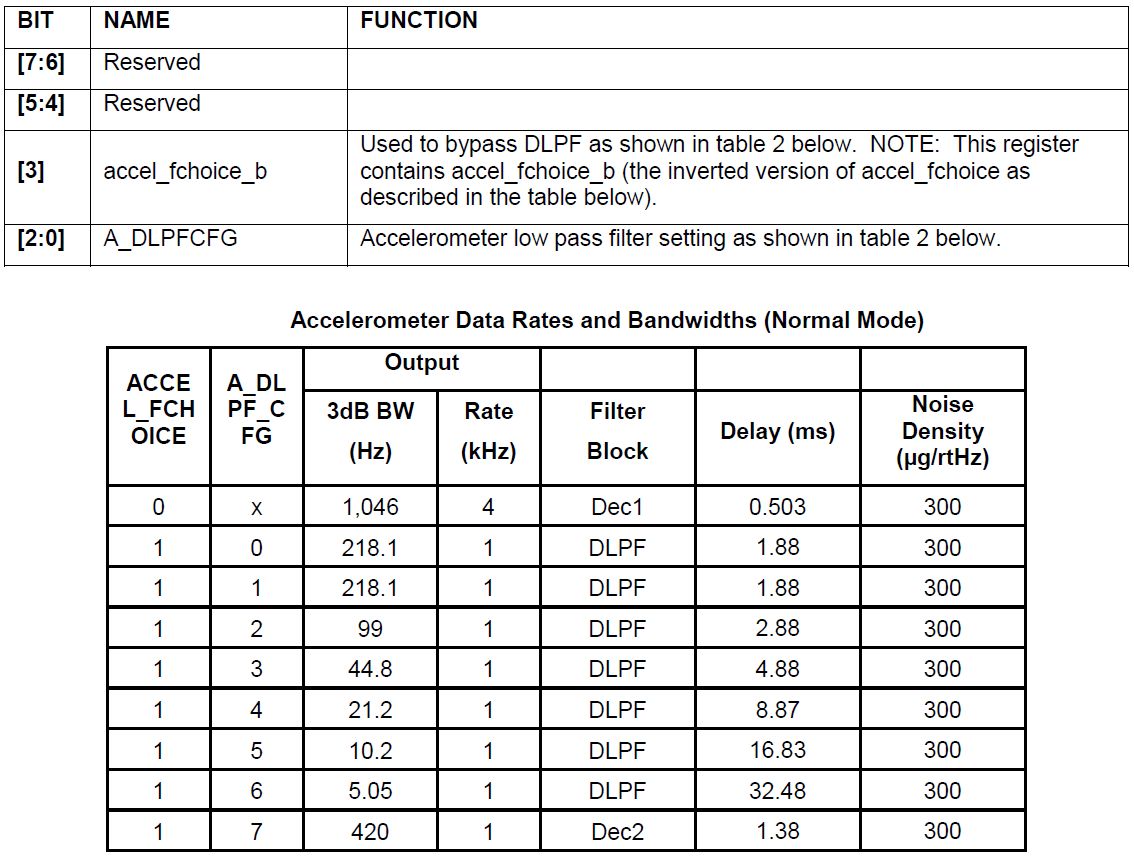
Легче не стало, так что пройдёмся прямо по списку.
Наследие Древнего Рима
Частота дискретизации + децимация $inline$Delta Sigma $inline$-АЦП = скорость обновления данных (digital output data rate, ODR)
С частотой дискретизации (она же частота семплирования) всё понятно — это количество взятых за секунду точек непрерывного по времени сигнала при его дискретизации АЦП. Измеряется в герцах.
$$display$$Fs=frac{1}{delta t}$$display$$
Для того, чтобы в выборку попало значение, приближенное к пиковой амплитуде сигнала, важно брать частоту дискретизации минимум в 10 раз больше частоты полезного сигнала. MPU-9250 предлагает три варианта Fs = 32kHz, 8kHz, 1kHz.
Но это абсолютно не значит, что сигнал на выходе акселерометра или гироскопа появляется с тем же периодом.
Если взять те же дроны, тут всё упирается в борьбу за снижение энергопотребления, повышение скорости вычислений и снижение шума выходных данных. Можно понизить частоту обновления данных на выходе, позволив внутренним алгоритмам интегрировать входную информацию в течение некоторого периода времени. Среднеквадратичный понизится, но также сузится и полоса пропускания (датчик сможет засечь лишь те процессы, частота которых будет меньше 50% скорости обновления данных).
Тут лучше сразу вспомнить теорему Котельникова. Она обещает, что при дискретизации аналогового сигнала можно избежать потерь информации (то есть восстановить сигнал без искажений), если частота полезного сигнала будет не больше половины частоты дискретизации, называемой также частотой Найквиста. На практике классический антиалайзинговый фильтр (фильтр низких частот, уменьшающий вклад побочных частотных компонентов в выходном сигнале до пренебрежимо малых уровней — ГОСТ Р 8.714-2010) требует в большинстве случаев разницу минимум в 2.5 раза [Siemens].
Для Fs = 32kHz частота Найквиста будет 16kHz. При этом полезный сигнал вряд ли выйдет за полосу fa = 20Hz (мало кто может менять направление движения чаще 20 раз в секунду). Итого, частота дискретизации значительно превышает частоту, требуемую для сохранения информации, содержащейся в полосе fa (40Hz, в 400 раз превышает), то есть полезный сигнал избыточно дискретизирован. Полоса между частотами fa и fs-fa не содержит никакой полезной информации. Можно уменьшить частоту дискретизации (на диаграмме это сделано с коэффициентом М, [7]), проредив последовательность семплов (отсчётов). Этот процесс и называется децимацией.
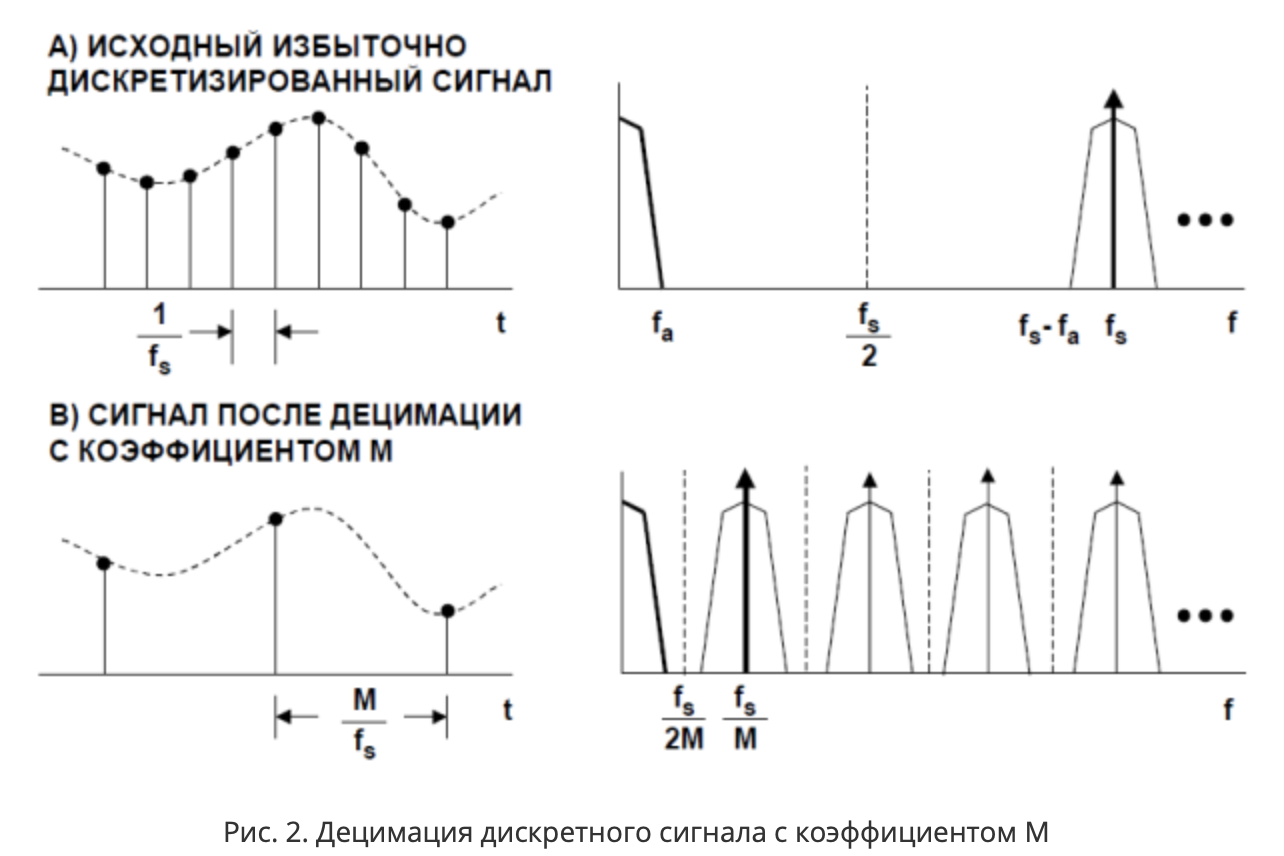
Согласно спецификации на MPU-9250, акселерометры снабжены сигма-дельта АЦП. Схемы на его основе потребляют минимальную мощность. Надо отметить, что полоса пропускания у данных преобразователей весьма узкая, не превышает звукового диапазона [Easyelectronics], но для штатного квадрокоптера больше и не нужно. Состоят они из двух блоков: $inline$ Sigma Delta $inline$-модулятора и цифрового децимирующего фильтра низких частот.
Зачем объединять фильтр низких частот и децимацию?
Честная выдержка из Вики:
Если исходный сигнал не содержит частот, превышающих частоту Найквиста децимированного сигнала, то форма спектра полученного (децимированного) сигнала совпадает с низкочастотной частью спектра исходного сигнала. Частота дискретизации, соответствующая новой последовательности отсчётов, в N раз ниже, чем частота дискретизации исходного сигнала.
Если исходный сигнал содержит частоты, превышающие частоту Найквиста децимированного сигнала, то при децимации будет иметь место алиасинг (наложение спектров).
Таким образом, для сохранения спектра необходимо до децимации удалить из исходного сигнала частоты, превышающие частоту Найквиста децимированного сигнала. В спецификации на MPU-9250 не очень много информации о характеристиках DLPF, но можно найти исследования энтузиастов [9].
Bandwidth, она же frequency response (частотный отклик)
диапазон частот, в котором датчик обнаруживает движение и выдает действительный выходной сигнал. В некоторых спецификациях приводится частотная характеристика датчика — зависимость электрического выходного сигнала акселерометра от внешних механических воздействий с фиксированной амплитудой, но различными частотами. В пределах полосы пропускания неравномерность частотной характеристики не превышает заданной. В случае применения цифрового фильтра низких частот выбор полосы пропускания как раз позволяет изменять частоту среза, неизбежно оказывая влияние на скорость отклика датчика на изменения положения в пространстве. Частота среза обязана быть меньше половины скорости оцифровки (digital output data rate, ODR), называемой также частотой Найквиста.
Для акселерометров MPU-9250 границы полосы пропускания определяются так, чтобы внутри диапазона спектральная плотность сигнала отличалась от пиковой (на частоте 0 Гц) не больше, чем на -3дБ. Этот уровень примерно соответствуют падению до половины спектральной плотности (или 70.7% от пиковой спектральной амплитуды). Напомню, для энергетических величин (мощность, энергия, плотность энергии), пропорциональных квадратам силовых величин поля, выраженное в децибелах отношение
$$display$$D_P = 10 lg{P_2 over{P_1}}$$display$$
.
Итог: сигналы, прошедшие через ФНЧ, менее зашумлены, у них лучшее разрешение, но при этом меньшая полоса пропускания. Поэтому указание разрешения в спецификации без привязки к полосе пропускания смысла не имеет.
Вернёмся к разрешению
В спецификации на MPU-9250 сведений о разрешении в принципе нет, для BMI088 под именем «Разрешение» представлены цифровое разрешение (LSB) и чувствительность»:
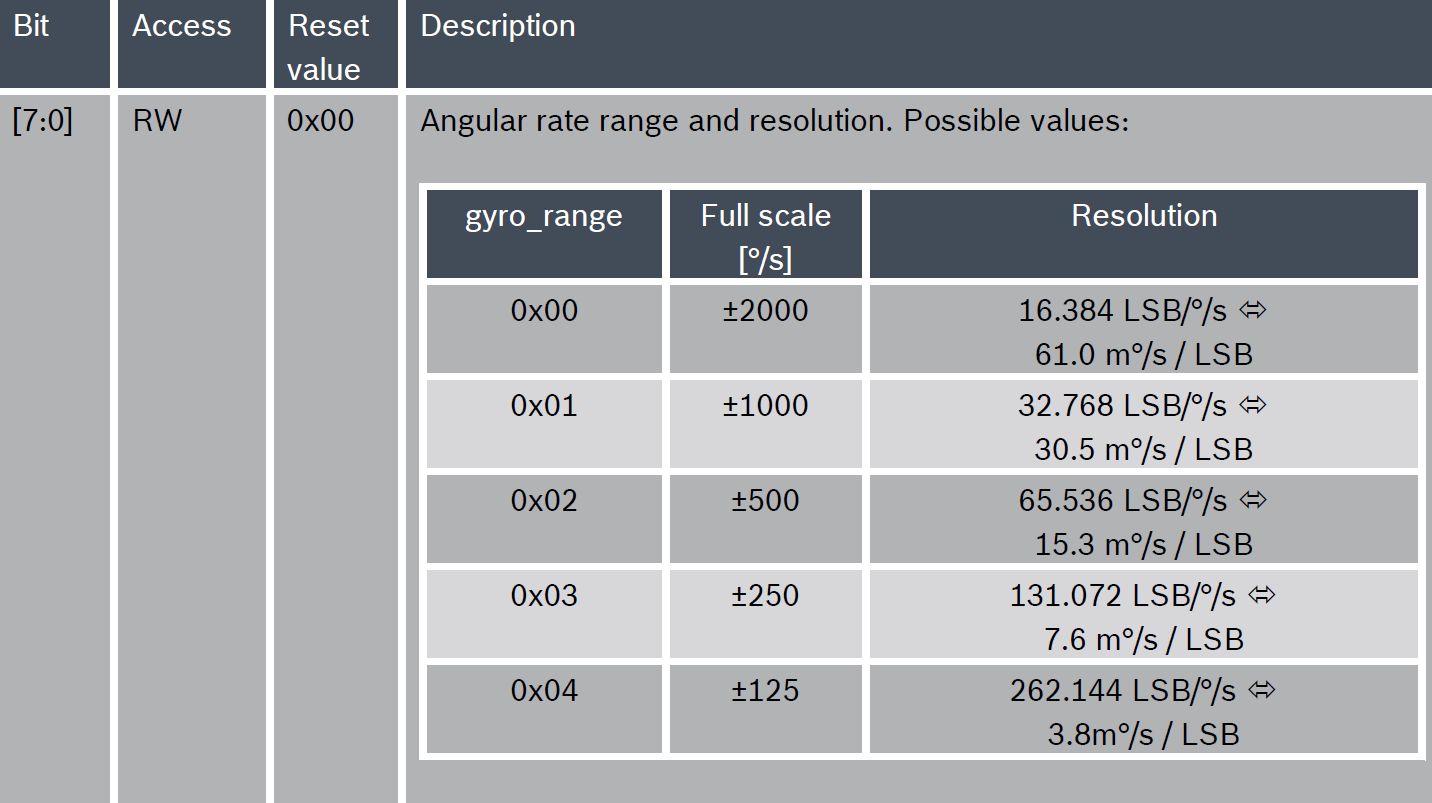
Оценить разрешение для каждой полосы пропускания можно по пиковому шуму $inline$Noise_{pk-pk} = Total Noise_{RMS} times CrestFactor = Total Noise_{RMS}times 4.$inline$ Среднеквадратичная величина шума на выходе связана с указанной в спецификации спектральной плотностью (а вернее, корнем из неё) и эквивалентной шумовой полосой пропускания (equivalent noise bandwidth, ENBW, — полоса пропускания эквивалентной системы, имеющей прямоугольную АЧХ и одинаковые с исходной системой значение на нулевой частоте и дисперсию на выходе, при воздействии на входы систем белого шума):
$$display$$N_{RMS} = PSD times sqrt{ENBW}$$display$$
А шумовая полоса пропускания связана с 3dB полосой коэффициентами, соответствующим порядку низкочастотного фильтра:
$$display$$ENBW = 1.57cdot f_{3dB} textrm{ для 1-го порядка}$$display$$
$$display$$ENBW = 1.11cdot f_{3dB} textrm{ для 2-го порядка}$$display$$
$$display$$ENBW = 1.05cdot f_{3dB}textrm{ для 3-го порядка}$$display$$
$$display$$ENBW = 1.025cdot f_{3dB}textrm{ для 4-го порядка}$$display$$
Судя по исследованию в [MPU9250_DLPF], наш выбор 1.57. Полученное среднеквадратическое значение учитывает вклад белого шума (ни шума квантования, ни механического шума там нет). Например, для акселерометра расчётное значение для $inline$BW = 99Hz, PSD = 300mu g/sqrt{Hz}$inline$ получается $inline$N_{RMS} = 4mg$inline$. При этом в спецификации отдельно указан полный среднеквадратичный шум $inline$Total RMS Noise = 8mg.$inline$ Расхождение значительное. К сожалению, он указан лишь для одной полосы, а для акселерометра BMI088 в спецификации указано только PSD. Так что будем использовать что есть. Кросс-фактор возьмём 4. Теперь самое интересное. Отношение $inline$FS/Noise_{pk-pk}$inline$ даст примерный порядок эффективных бит на данном диапазоне измерений, который прилично меньше 16-битного разрешения АЦП.
| MPU-9250 | BMI088 | ||||
|---|---|---|---|---|---|
| Гироскоп | |||||
| $inline$small N^{Total}_{RMS} = 0.1^{circ}/s (BW=92Hz)$inline$ | $inline$small N_{RMS} = 0.1^{circ}/s (BW=47Hz)$inline$ | ||||
| $inline$small PSD=0.01^{circ}/s/sqrt{Hz}$inline$ | $inline$small PSD=0.014^{circ}/s/sqrt{Hz}$inline$ | ||||
| $inline$small BW, Hz$inline$ | $inline$small N_{RMS}, ^{circ}/s-rms$inline$ | $inline$small N_{PP}, ^{circ}/s $inline$ | $inline$small BW, Hz$inline$ | $inline$small N_{RMS}, ^{circ}/s$inline$ | $inline$small N_{PP}, ^{circ}/s $inline$ |
| 523 | 0.41 | 1.6 | |||
| 250 | 0.2 | 0.8 | 230 | 0.27 | 1.1 |
| 184 | 0.17 | 0.69 | 116 | 0.19 | 0.76 |
| 92 | 0.12 | 0.49 | 64 | 0.14 | 0.57 |
| 41 | 0.08 | 0.32 | 47 | 0.12 | 0.49 |
| 20 | 0.06 | 0.23 | 32 | 0.1 | 0.4 |
| 10 | 0.04 | 0.16 | 23 | 0.09 | 0.34 |
| 5 | 0.03 | 0.11 | 12 | 0.06 | 0.25 |
| Акселерометр | |||||
| $inline$small N^{Total}_{RMS} = 8mg textrm{ (BW=99Hz)} $inline$ | $inline$small PSD_{XY}=160mu g/sqrt{Hz}$inline$ | ||||
| $inline$small PSD=300mu g/sqrt{Hz} textrm{ (Gyro off)}$inline$ | $inline$small PSD_Z = 190mu g/sqrt{Hz} (g_{FS3g}, textrm{ Normal mode})$inline$ | ||||
| $inline$small BW, Hz$inline$ | $inline$small N_{RMS}, mg$inline$ | $inline$small N_{PP}, mg $inline$ | $inline$small BW, Hz$inline$ | $inline$small N_{RMS_XY}, mg$inline$ | $inline$small N_{PP_XY}, mg$inline$ |
| 218.1 | 5.6 | 22 | 280 | 3.4 | 14 |
| 99 | 3.8 | 15 | 145 | 2.4 | 10 |
| 44.8 | 2.5 | 10 | 80 | 1.8 | 7 |
| 21.2 | 1.7 | 7 | 40 | 1.3 | 5 |
| 10.2 | 1.2 | 4.9 | 20 | 0.9 | 4 |
| 5.05 | 0.9 | 3.4 | 10 | 0.6 | 2.6 |
| 420 | 7.8 | 31 | 5 | 0.5 | 1.8 |
| 1046 | 12.3 | 49 | |||
Delay (ms), или откуда берётся задержка
Из необходимости сохранять во внутреннем буфере переменные для деления фильтром сигнала на разные частоты
Итого. Чем ниже частота обрезания фильтра, тем меньше шума в сигнале. Но тут надо быть осторожным, потому что одновременно с этим вырастает и задержка. Кроме того, можно пропустить полезный сигнал [8].
| MPU-9250 | BMI088 | ||
|---|---|---|---|
| Гироскоп, 16 бит | |||
| Диапазон (FS), $inline$^{circ}/s$inline$ (dps) | Разрешение, бит (BW=92Hz) | Диапазон (FS), $inline$^{circ}/s$inline$ (dps) | Разрешение, бит (BW=64Hz) |
| $inline$pm 125$inline$ | 8 | ||
| $inline$pm 250$inline$ | 9 | $inline$pm 250$inline$ | 9 |
| $inline$pm 500$inline$ | 10 | $inline$pm 500$inline$ | 10 |
| $inline$pm 1000$inline$ | 11 | $inline$pm 1000$inline$ | 11 |
| $inline$pm 2000$inline$ | 12 | $inline$pm 2000$inline$ | 12 |
| Акселерометр | |||
| Диапазон (FS), g | Разрешение, бит $inline$(N_{PP}=32mg)$inline$ | Диапазон (FS), g | Разрешение (по X,Y), бит $inline$(N_{PP}^XY=14mg)$inline$ |
| $inline$pm 2$inline$ | 6 | $inline$pm 3$inline$ | 8 |
| $inline$pm 4$inline$ | 7 | $inline$pm 6$inline$ | 9 |
| $inline$pm 8$inline$ | 8 | $inline$pm 12$inline$ | 10 |
| $inline$pm 16$inline$ | 9 | $inline$pm 24$inline$ | 11 |
И это лишь самые основные параметры.
Откуда что бралось:
- Самый приятный документ от Freescale Semiconductor — «How Many Bits are Enough?»
- [EE] — «Resolution vs Accuracy vs Sensitivity Cutting Through the Confusion»
- [Время электроники] — «МЭМС-датчики движения от STMicroelectronics: акселерометры и гироскопы»
- [LSB] — «An ADC and DAC Least Significant Bit (LSB)»
- [Measurement Computing] — «TechTip: Accuracy, Precision, Resolution, and Sensitivity»
- [KIT] — «Акселерометры Analog Devices — устройство и применение»
- [Easyelectronics] — «Сигма-дельта АЦП»
- [Радиолоцман] — «Магнитометры: принцип действия, компенсация ошибок»
- [SO] — «Noise Measurement»
- [Mide] — «Accelerometer Specifications: Deciphering an Accelerometer's Datasheet»
- [CiberLeninka] — Delta-Sigma ADC Filter
- [SciEd] — «Особенности реализации цифровой фильтрации с изменением частоты дискретизации»
- [MPU6050] — «Using the MPU6050’s DLPF»
- [MPU9250_DLPF] — MPU9250 Gyro Noise DLPF work investigation
- Understanding Sensor Resolution Specifications
- Siemens Digital Signal Processing
- МЭМС-датчики движения от STMicroelectronics
- [TMWorld] — «Evaluating inertial measurement units»
- [Sklyar] – Скляр Б. Цифровая связь. Теоретические основы и практическое применение.
Автор: RuthHieris






