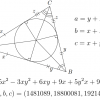
Работа Александра Смита по гипотезе Голдфелда раскрыла фундаментальные свойства эллиптических кривых
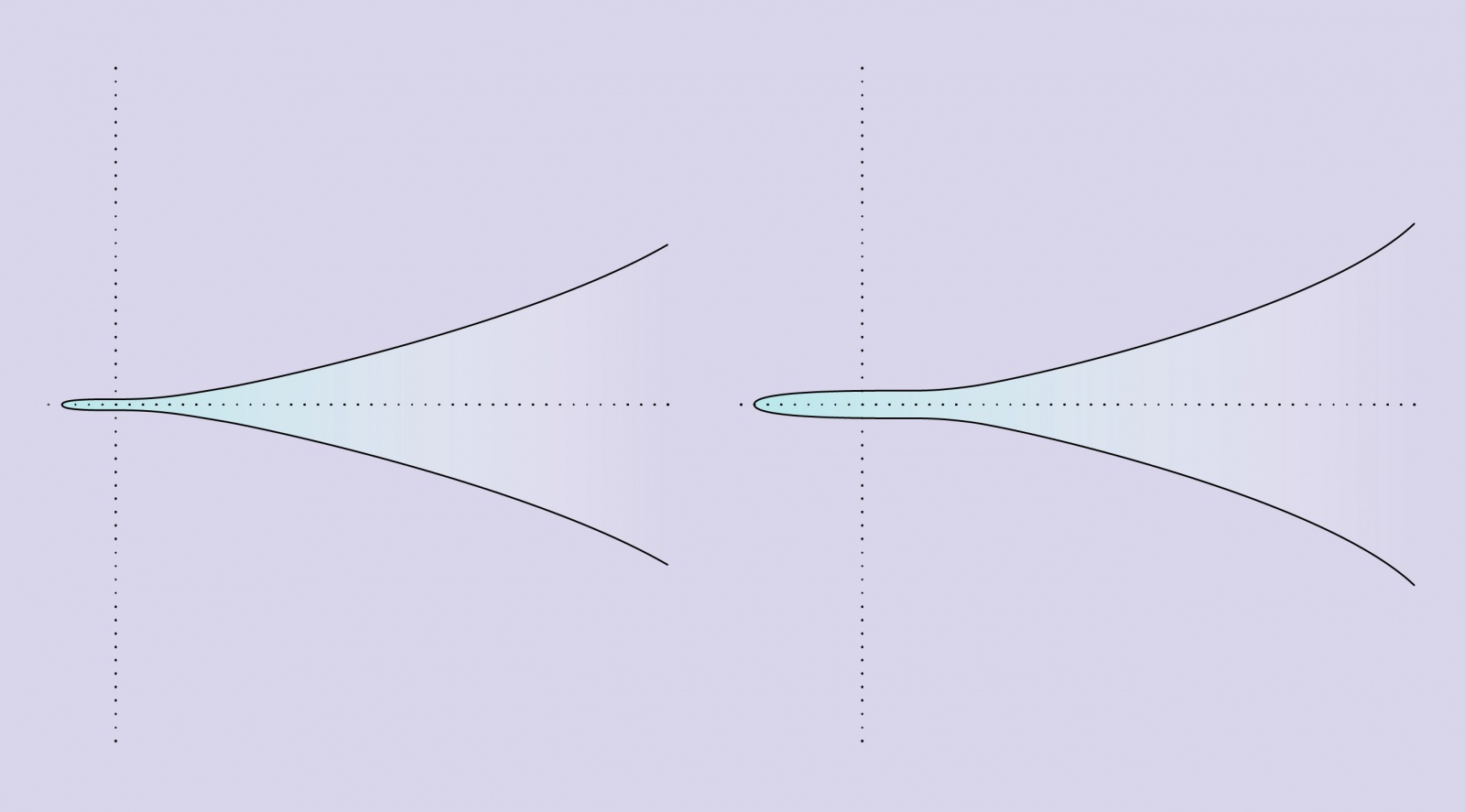
Две эллиптические кривые демонстрируют странности концепции ранга. Кривая слева описывается уравнением y2 = x3 + 1, проходит только через пять рациональных точек и имеет ранг 0. Кривая справа описывается уравнением y2 = x3 + 8, проходит через бесконечное число рациональных точек, и имеет ранг 1.
Вариантов эллиптических кривых может быть много, но их реальных разновидностей всего две. Таков итог нового доказательства, полученного аспирантом из Гарвардского университета.
Эллиптические кривые кажутся чем-то экзотическим, однако это непримечательные геометрические объекты, не сложнее прямых, парабол или эллипсов. В своей работе, опубликованной в онлайне в прошлом году, Алексадр Смит доказал гипотезу сорокалетней давности, касающуюся фундаментальной особенности эллиптических кривых, ранга. Смит доказал, что из определённого семейства кривых, имеющих одну характеристику, половина имеют ранг, равный 0, а половина – 1.
Этот результат устанавливает опорную характеристику объектов, занимавших математиков много веков, чья важность особенно возросла в последние десятилетия.
«Мы думали об этом более 1000 лет, и теперь у нас появилось вероятностное понимание эллиптических кривых. Это чрезвычайно важно», — сказал Шоу-У Чжан, математик из Принстонского университета, дававший Смиту рекомендации по его работе, когда тот был ещё студентом в Принстоне.
Эллиптические кривые – это уравнения с переменными, возведёнными в третью степень, например, y2 = x3 + 1. Они фигурировали во многих значимых математических доказательствах в последние десятилетия, включая важнейшее доказательство Великой теоремы Ферма от 1994 года. Часть их значимости состоит в том, что они принадлежат к самому сложному типу полиномиальных уравнений, о котором у математиков есть какие-то системные представления.
«Эллиптические кривые – это интересный случай», — сказал Дориан Голдфелд, математик из Колумбийского университета, предложивший в 1979 гипотезу, получившую его имя.
Гипотеза Голдфелда делает предсказания по поводу ранга эллиптических кривых. Как мы уже описывали в недавней статье "Какие свидетельства могут убедить математиков, если строгого доказательства нет?", ранг – это мера сложности набора рациональных решений кривой (решений, которые можно представить в виде дробей). И хотя не существует доказанного ограничения величины ранга кривой – пока что самым высоким рангом из обнаруженных считается величина 28 – гипотеза Голдфелда предсказывает, что в среднем у половины эллиптических кривых ранг равен 0, а у другой половины – 1.
Вам может показаться непонятным, как могут существовать эллиптические кривые рангом более 1, если у половины эллиптических кривых ранг равен 0, а у другой половины – 1. Если у вас есть коробка шариков для пинг-понга, и если вы знаете, что ровно половина из них чёрные, а половина – белые, то красных там быть не может.
Ещё сильнее запутывает тот факт, что эллиптических кривых с рангом 2 или выше существует не просто несколько, а бесконечное количество. Кажущийся абсурдным результат является следствием хитрой статистики, работающей с бесконечностями. Даже несмотря на то, что кривых рангом 2 и выше есть очень много, кривых с рангами 0 и 1 настолько больше, что кривые с рангами 2 и выше статистически не имеют значения. Если сложить все кривые в коробку и вынимать их оттуда случайным образом, то шансы вытащить кривую с рангом более 1 официально приравниваются к нулю.
Что означает, что ранг кривой равен 0? У таких кривых есть конечное количество рациональных точек – причём не более 16, как доказал ещё Барри Мазур в 1970-х.

Дориан Голдфелд
Есть причины полагать, что у очень большого количества эллиптических кривых ранг будет равен 0. Если представить, как кривая бежит по плоскости, будет видно, что большая часть точек, через которых она проходит, не будут рациональными. Эти точки нельзя выразить в виде дробей, пусть даже сколь угодно сложных. Шансы на то, что случайная кривая пересечёт множество рациональных точек – бесконечное множество – малы.
«Я отношусь к этому так: если взять случайную эллиптическую кривую, то у неё будут причины иметь ранг 0. Она не хочет иметь рациональных точек», — сказал Смит.
Распространённость кривых ранга 1 объясняется сходным образом. У кривых ранга 1 есть бесконечно много рациональных точек, однако все они очень аккуратно выстраиваются, так, что соединять их друг с другом можно в рамках довольно простого процесса.
У кривых рангом 2 и выше наборы рациональных точек устроены сложнее. В них содержатся несколько бесконечных подмножеств рациональных точек, не связанных друг с другом.
«Каковы шансы на появление двух независимых точек? – сказал Голдфелд. – Весьма низки. Моя гипотеза говорит, что такое должно происходить редко».
Когда Голдфелд впервые выдвинул свою гипотезу, большинство математиков посчитали её неверной. Они указывали на результаты вычислительных экспериментов, из которых следовало, что кривые с рангом 2 или выше возникают гораздо чаще, чем в 0% случаев.
Голдфелд ответил, что они просто забрасывают недостаточно широкую сеть. Он указал, что если изучать только первые 10 целых чисел, то можно получить чрезвычайно неточную оценку того, что 40% чисел являются простыми. Точно так же эти вычислительные эксперименты экстраполировали от небольших подмножеств эллиптических кривых к бесконечно большим семействам кривых.
«Я сказал – посмотрите на простые числа! Таков был мой ответ. Нужно забираться гораздо выше, потому что в начале может появляться много забавного», — сказал Голдфелд.
Гипотеза Голдфелда относится не ко всем эллиптическим кривым. Она описывает особое семейство эллиптических кривых, квадратичные изгибы [quadratic twists]. Пример: эллиптическая кривая cy2 = x3 − x, где c – некая константа. Изменяя значение c, вы изгибаете эллиптическую кривую. Гипотеза Голдфелда относится ко всему бесконечному разнообразию кривых, которое можно получить, изменяя значение c.
Александр Смит показал, что Голдфелд был прав. В новой работе он доказывает, что 100% эллиптических кривых (особого рода) имеет ранг 0 или 1. Он т акже доказал, что эти кривые поровну разделяются между двумя рангами, хотя тут есть и подвох. Его доказательство разделения 50 на 50 основывается на справедливости гипотезы Бёрча — Свиннертон-Дайера (БСД). Гипотеза БСД – одна из известнейших открытых проблем математики. Математики пока и близко не подошли к её доказательству, но в целом считают её верной.
Даже с такой оговоркой, результат Смита считается весомым. Математики говорят, что он показывает способ полностью доказать гипотезу Голдфелда, не возясь с обескураживающей гипотезой БСД. Этот способ даёт новое понимание природы эллиптических кривых.
«Работа Алекса Смита чрезвычайно интересна, и я думаю, её ещё предстоит как следует изучить и воздать по заслугам», — сказала Мелани Вуд, математик из Висконсинского университета. «То, что это можно доказать – это очень важно и революционно».
Автор: SLY_G