В недавней статье товарищ KvanTTT поднял вопрос:
Можете пояснить что вам не нравится в современной записи (математических положений и) формул и как ее можно улучшить?
Я постарался ответить в одном комментарии, но размер текстового поля не позволил закончить выкладки. Данная статья — чрезмерно развернутый ответ.
Сразу скажу, материал холиварный. Местами слишком эмоциональный. Очень спорный. Слишком личный — часто основан на собственном опыте, небогатом, хоть и разнообразном. Пост касается школьных и университетских текстов учебников: у «профессиональной» литературы своя специфика, своя аудитория. Решения у проблемы в текущих реалиях нет. При этом, часть «моих» наблюдений задолго до меня высказывали такие авторитеты, как Кнут и Хэмминг; чуть менее популярные ребята даже запилили инструкцию "Как читать математику".
Итак, на мой взгляд, основные претензии не столько к записи формул, сколько к подаче материала. Причем, к подаче материала на практически всех уровнях образования, начиная со школы, и заканчивая передовой наукой. Начало текущей ситуации положил Евклид, заявивший про отсутствие царской дороги в математике. Царскую дорогу не проложили до сих пор. Евклид обходился, и мы сможем.
Первая проблема — значимость не показана. Еще один подарок от Евклида: «Дай вопрошающему грош, если он ищет выгоды, а не математики». Авторы начинают вводить определения, доказывать теоремы и творить прочую математику без объяснения зачем оно вообще нужно. Пример: учебник по математическому анализу от Фихтенгольца. Почитайте первую главу: «из школьного курса вы знаете про рациональные числа, но потребности математики понуждают нас ввести вещественные...» и понеслась. Какие потребности, какой математики, чем не устраивают рациональные — да пес его знает. «Очевидно».
Или другой пример из того же учебника. «Постоянное число a называется пределом варианты 
если для каждого положительного 
сколько бы мало оно ни было, существует такой номер N, что все значения 
, у которых номер n>N, удовлетворяет равенству 
.»
Большинство студентов не понимает определения выше, но через полгода привыкает к нему. Еще больше студентов даже к концу обучения не осознает, зачем им было нужно понятие предела последовательности. Аналогично для функций, интегралов, рядов… Фихтенгольц описывает какие-то математические объекты, иногда дает частные примеры — и все. Ну да, сейчас мне понятно, что пределы нужны, например, для корректного описания верхних/нижних сумм при введении интегралов, но до интегралов еще два семестра!
Или определитель, определяемый как кососимметрическая полилинейная функция. Ребята, вы это серьезно? Единственный адекватный ответ студента-первокурсника на такой определение «и что»? Выгода какая с этого определения? Не спорю, выгода есть, но всякий ли первокурсник может её осознать?
Ложное решение проблемы: история вопроса. Проявляется на всякого рода конференциях. «Проблему поставил Иаков, исследовал его ученик Авель, и ученик ученика Каин, и сто-пятьсот воплощений Вишны». В чем суть проблемы, почему её решал первоначальный автор, почему так важно убивать на неё профессоро-часы — опускается.
Следующая проблема — авторы не ставят реальных проблем
В принципе, схожа с предыдущей. Вспомните курс теории вероятностей. Какие там преобладают задачи? «В корзине лежат 25 черных и 10 белых шаров...». Казиношные примеры, карточные, D&D, экономические — не, не слышали. Мы будем использовать максимально политкорректные примеры, хоть теория вероятностей выросла из исследований игры в кости.
Про живые примеры недавно писала Free_Mic_RS
Математика начинается с задачи. И мертвые, однобокие задачи оставляют впечатление, что теор-вер только с ними и работает. Намерение авторов благое: дать пример, а потом перейти к общему. Абстрагировать от примера. Но несколько «живых» примеров сделали бы переход к абстракции гораздо полезнее. По крайней мере, я свято верю, что обратный процесс (переход от абстрактного к частному) проходил бы гораздо проще.
Проблема: излишняя краткость и непоследовательность
Помните школу? А формулу дискриминанта? А как она доказывается/выводится? Один из способов: чисто алгебраический. Берем уравнение 
, «Умножаем каждую часть на 
и прибавляем 
» (почему именно на эти значения?), еще немного трансформаций — и готово. После дискриминанта ученикам дают дискриминант-для-четного-b. А потом формулы Виета. А ещё полные квадраты. И кучу примеров. И далеко не всегда объясняется, зачем нужны все эти методы.
А теперь представьте ситуацию, ученику говорят: «сегодня мы научимся решать уравнения с 
. Любые.» И начинается серия примеров с усложнением.
Очень много примеров, которые органично приводят к решению уравнения через полные квадраты. Потом уже можно вводить дискриминант (как простой алгоритм для решения уравнений, когда ученики устанут выделять полные квадраты), и Виет с четным дискриминантом как «ноу-хау».
Схожий подход используется в учебниках. Увы, не во всех. И не везде видна четкая последовательность. По слухам, некоторые авторы теряли листы черновиков в трамваях, а потом заменяли утерянные куски выражениями вроде «легко показать, что...». В итоге, вместо спокойных прыжков с примера на пример, студенты были вынуждены перепрыгивать через пропасть. Сколько людей сорвалось и еще сорвется за 10+6 лет обучения в школе/ВУЗе?
Личный пример (просили в оригинальном посте). На первом курсе матана я страдал. Спокойно решая примеры, совершенно не усваивал теорию. Попросил однокурсника о помощи с вычислением длины кривой через интеграл. Тот взял бутылку пива, нарисовал рандомную кривую, спрямил бесконечно малыми отрезками, выделил один такой отрезок, достроил его до треугольника dl, dx, dy, и спросил: «Теорему Пифагора помнишь»? Дальше все было просто.
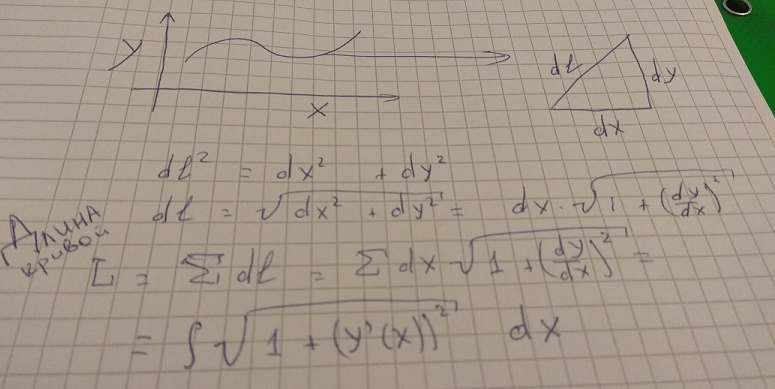
Я его спросил: а почему такое не показывают на парах/в учебниках? Он показал пару контрпримеров, объяснил зачем нужен формализм в матане — и у меня попёрло. Я просто читал теорему, выделял главное, писал/решал тривиальные примеры, потом разбирался с формализмом — и реально понимал, о чем идет речь.
Я не знаю, можно ли массово использовать подход общий обзор => контрпримеры => формализм. Не знаю, сколько и какой теории/практики нужно набрать студенту до «прорыва», с трудом представляю себе, как ставить педагогические эксперименты на эту тему, и сколько труда придется вложить в исследования. Но память о том объяснении живет уже 10 лет. И спустя все эти годы я стараюсь слушателям сначала дать общую картину, потом показать проблемы, и потом уже погружаться в детали.
Вы скажете, мои персональные ощущения могут быть ошибочными. Помимо них у меня есть только аналогичные идеи от Хэмминга:
… я мог изучать, какие методы были эффективны, а какие нет. Посещая встречи, я уже изучал, почему некоторые работы запоминают, а большинство – нет. Технический человек хочет дать очень ограниченную техническую лекцию. Как правило, аудитория хочет широкую лекцию общего характера и хочет гораздо больше общего обзора и введений, чем желает дать спикер. В результате многие лекции неэффективны. Лектор называет тему и внезапно ныряет в детали. Мало кто может уследить. Вы должны нарисовать общую картину, чтобы рассказать, почему это важно, и затем медленно развернуть эскиз того, что было сделано. Тогда большее число людей скажут: «Да, Джо сделал это» или «Мэри сделала то, я действительно вижу, о чём это. Да, Мэри дала по-настоящему хорошую лекцию, я понимаю, что она сделала». Как правило же, люди дают очень ограниченную, безопасную лекцию; это обычно неэффективно. Кроме того, многие лекции переполнены информацией…
Идеи россыпью
Должен заметить, мой опыт в преподавании крайне ограничен. Возможно, вы заметили, что я ограничился школьной программой и матанализом. Увы, это те области, где у меня была возможность соприкоснуть теорию с практикой. Я до сих пор не понимаю сути определителя в алгебре, не осознаю проективную геометрию, и лишь полгода назад начал проникаться матрицами (сразу после практики, ага). Неплохая иллюстрация поговорки «теория без практики мертва».
Как мне рассказывали, в НМУ новый концепт всегда вводился с десятком вопросов. А что если так? А если этот пункт условия не выполнен? Что нужно, чтоб дополнить наш концепт до полугруппы? Слушателям давали поиграть с предметом. Привыкнуть. Думаю, над опытом НМУ стоит хорошенько задуматься.
Наверняка в высших разделах математики подход «сначала пример, потом абстракция» не сработает. Так, примеры «на бумажке» никак не помогают осознать RSA. Зато растущее время работы программы с увеличением длины ключа помогает прочувствовать чисто практические аспекты.
Есть опасение, что «идеальные/тепличные» школьные учебники приведут к шоку при работе с «вышкой». Вроде как, «хардкорщика надо воспитывать смолоду».
Довольно сложно разрабатывать курсы, надеясь что студенты уже что-то знают. Чем больше требуемая база, тем больше вероятность, что что-то из базы студентом недопонято.
Говорят, пик формы математиков — 30 лет. После 30 уже можно нагружать их писать учебники, дав в напарники спеца методиста.
Текущие технологии позволяют писать тексты командой, используя git. На хабре недавно проскакивала статья про компиляцию TeXa в pdf в процессе CI. Уверен, авторский коллектив с хорошим инструментарием может писать гораздо более качественные учебники.
Помимо профессоров, учителей, студентов и школьников в математике есть государства. И регламенты. И требования. И сертификации. Все это влияет на учебники, авторов, преподавателей, и качество подачи материала.
Как можно улучшить подачу материала в математических текстах
В текущих (российских) реалиях — никак. Энтузиасты есть, профессионалы есть, мотивации нет.
У профессоров математики хватает своих задач, чтобы писать учебники. Иногда не хватает чисто гуманитарных скиллов, писать книги в университетах не учат. Плюс, профессиональная деформация: «очевидное» для профессора может быть неподъёмно для студентов. Учителя математики загружены текучкой. И бумагами. И репетиторством. Про государство промолчу. Почти не сталкивался с его представителями, так что говорить нечего. Разве что, упомяну политику замену учебников каждые три года. После школы я хотел сдать свои учебники в библиотеку, мне сказали «они старые, нельзя их хранить». Мотивации писать хорошие учебники такой подход не добавляет.
Иными словами, от системы образования лично я позитивных подвижек не жду. Надеюсь, конечно, но не жду. Что выручает — проблески ИТ и прочей инженерии. На одной из математических конференций я получил от одного из участников книгу по компьютерной графике. Автор работал в конторе, разрабатывающей графическое ядро какой-то чертежной системы, и материал был вполне неплох. Математика была не «чистая», прикладная, но сам факт существования хорошего учебного материала безусловно радует.
Еще один подход: преподаватели от компаний, работающие в ВУЗах. Математических текстов от этих ребят ждать не приходится, специфика не та. Разве что, геймдевщики соберутся написать мануал по теорверу, или графики напишут про алгебру/геометрию необходимую для разработки тех же САПРов (если такие проекты есть — зовите).
Наконец, есть различные негосударственные образовательные платформы, вроде той же Coursera. Эти ребята могут все, ибо работают за деньги, конкурируют, быстро получают обратную связь. Но у них свой недостаток: формат подачи данных иной. Непосредственно текстов они не пишут.
И к чему все придет в будущем?
Самому интересно. Может, всё останется как есть. Может, будет уход от текстов в математике. А может, авторы проникнутся идеей "продукт текст должен быть удобным для клиента читателя", и силами первопроходцев удастся таки переломить традицию. Тогда лет через 30-50-100 у нас появятся учебники, понятные большинству читателей.
Upd1. Вставил фото с вычислением длины участка кривой.
Upd2. В комментариях часто упоминают, что текст посвящен проблемам преподавания, а не профессиональной математике. Причина проста: большая часть виденных мною «профессиональных» работ в плане подачи материала не отличается от учебников. При этом, школьнаяуниверситетская литература известна большинству на хабре, а «профессиональная» — процентам.
Автор: Oxoron
