Намедни прочел интересную статью про рейтинги. В качестве практического руководства ее не рекомендую использовать (почему смотрите в комментариях к ней), однако, чтиво интересное и натолкнуло меня на одну мысль.
Допустим у нас есть рейтинг от 1 до 5. И некоторые оценки накручены, некоторые пользователи наобум поставили. Как отфильтровать зерна от плевел?
Если построить диаграмму количества человек поставивших определенную оценку, то можно увидеть примерно сколько голосов было накручено. Нужно, конечно, сравнивать с другими диаграмами, но из этой картинки понятно что часть «пятерок» накручено:
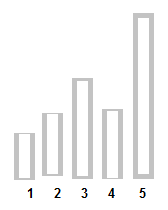
В общем человек может по диаграмме определить накрутку, значит и машина тоже сможет.
Распределение голосов можно расписать функцией бета распределения.
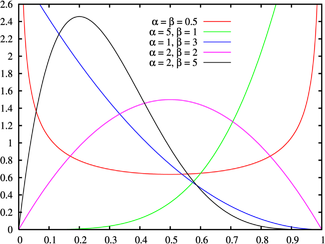
Если в большинстве случаев голосование можно описать бета-функцией, а в части нельзя, то можно убрать часть голосов.
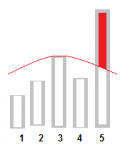
Таким образом мы не исключим все плохие голоса, исключим часть хороших. Для статей с малым числом голосов такие манипуляции недопустимы.
Бета-распределение имеет два параметра, альфа и бета. У нас тоже есть два параметра средняя оценка(E) и дисперсия(D) — мера разброса. Из википежии известно, что.
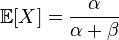
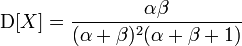
Теперь решим систему уравнений. Это долго и нудно.
E=a/(a+b)
d=ab/((a+b)^2 * (a+b+1))заменим a/(a+b) на E
d=bE/((a+b) * (a+b+1))заменим 1/(a+b) на E/a
d=b*E^2/(a * (a+b+1))умножим обе части на (a * (a+b+1))
d(a * (a+b+1))=b*E^2раскроем скобки и поменяем местами
b*E^2=da^2 + dab + daвычтем dab из обоих частей
b*E^2-dab=da^2 + da
b(E^2-da)=da(a+1)
b=da(a+1)/(E^2-da)
Вернемся к первому уравнению
E=a/(a+b)=>(a+b)=a/E=> b=a/E -a
объединим оба уравнения
b=a/E -a=da(a+1)/(E^2-da)
a/E -a=da(a+1)/(E^2-da)
разделим на а1/E -1=d(a+1)/(E^2-da)
умножим на E(E^2-da)
(1-E)(E^2-da)=Ed(a+1)
E^2-da -E^3 + Eda=Eda + Ed
Eda сократиться
E^2-da -E^3 = Ed
E^2 -E^3 -Ed =da
a= (E^2 -E^3 -Ed)/d
b=a/E -a=a(1/E-1)=a(1-E)/E=(E^2 -E^3 -Ed)(1-E)/Ed=(E -E^2 -d)(1-E)/d=(E -E^2 -d — E^2 + E^3 +dE)/d
b=(E^3-2E^2+E)/d +E -1
В итоге мы сможем построить бета-функцию. Все оценки выше нее, вероятные накрутки. Если кому-то будет интересно распишу подробнее.
Автор: Hkey



