Работа с числовыми матрицами в целом и решение систем линейных алгебраических уравнений в частности — классическая математическая и алгоритмическая задача, широко используемая при моделировании и расчёте огромного класса бизнес-процессов (например, при расчёте себестоимости). При создании и эксплуатации конфигураций «1С:Предприятия» многие разработчики сталкивались с необходимостью вручную реализовывать алгоритмы расчёта СЛАУ, а после — с проблемой длительного ожидания решения.
«1С:Предприятие» 8.3.14 будет содержать функционал, позволяющий значительно сократить время решения систем линейных уравнений за счёт использования алгоритма, основанного на теории графов.
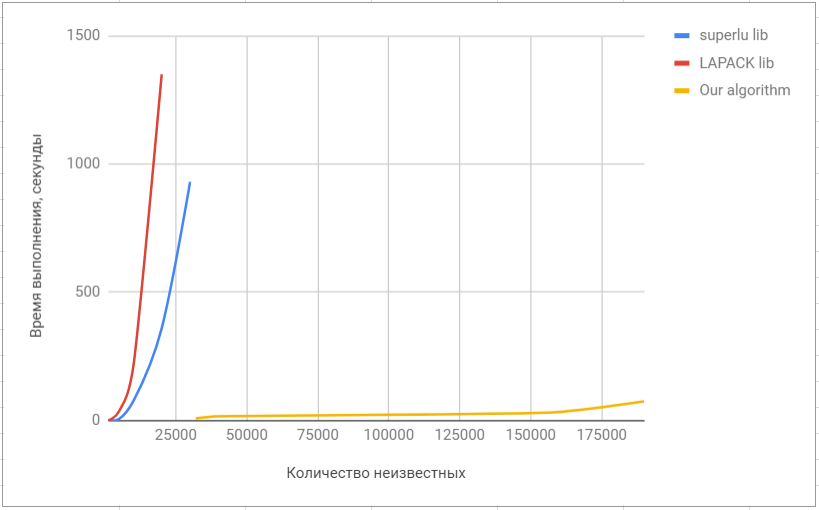
Он оптимизирован для использования на данных, имеющих разреженную структуру (то есть содержащие не более 10% ненулевых коэффициентов в уравнениях) и в среднем и в лучшем случаях демонстрирует асимптотику Θ(n⋅log(n)⋅log(n)), где n — количество переменных, а в худшем (при заполненности системы ~100%) его асимптотика сопоставима с классическими алгоритмами ( Θ(n3)). При этом на системах, имеющих ~105 неизвестных, алгоритм показывает ускорение в сотни раз по сравнению с реализованными в специализированных библиотеках линейной алгебры (например, superlu или lapack).
Важно: статья и описанный алгоритм требуют понимания линейной алгебры и теории графов на уровне первого курса университета.
Представление СЛАУ в виде графа
Рассмотрим простейшую разреженную систему линейных уравнений:

Внимание: система сгенерирована случайным образом и будет использоваться далее для демонстрации шагов работы алгоритма
При первом же взгляде на неё возникает ассоциация с другим математическим объектом — матрицей смежности графа. Так почему бы не преобразовать данные в списки смежности, сэкономив оперативную память в процессе выполнения и ускорив доступ к ненулевым коэффициентам?
Для этого нам достаточно транспонировать матрицу и установить инвариант “A[i][j]=z ⇔ i-я переменная входит в j-е уравнение с коэффициентом z”, а после для всякого ненулевого A[i][j] построить соответствующее ребро из вершины i в вершину j.
Полученный граф будет выглядеть так:
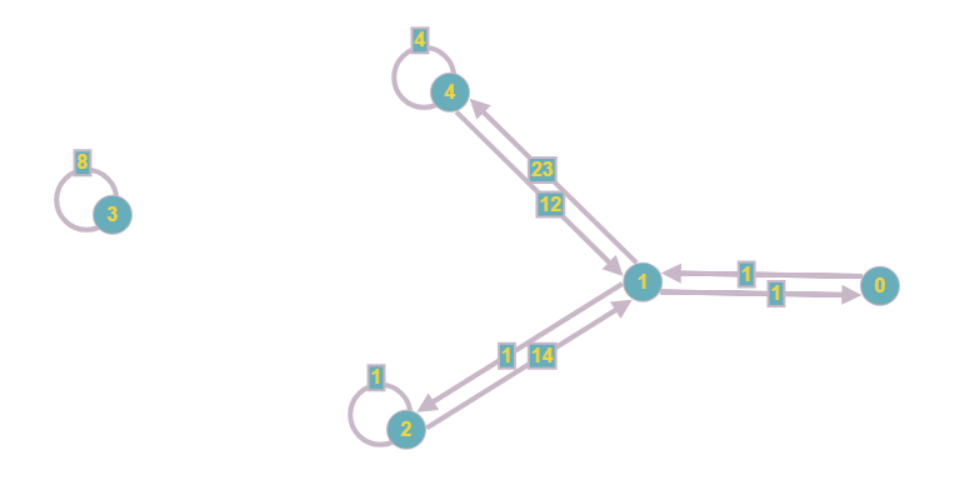
Даже визуально он оказывается менее громоздким, а асимптотические затраты оперативной памяти снижаются с O(n2) до O(n+m).
Выделение компонент слабой связности
Вторая алгоритмическая идея, которая приходит в голову при рассмотрении получившейся сущности: использование принципа “разделяй и властвуй”. В терминах графа это приводит к разделению множества вершин на компоненты слабой связности.
Напомню, компонента слабой связности — такое подмножество вершин, максимальное по включению, что между любыми двумя существует путь из рёбер в неориентированном графе. Неориентированный граф из исходного мы можем получить, например, добавлением к каждому ребру обратного (с последующим удалением). Тогда в одну компоненту связности будут входить все вершины, до которых мы можем дойти при обходе графа в глубину.
После разделения на компоненты слабой связности граф примет такой вид:
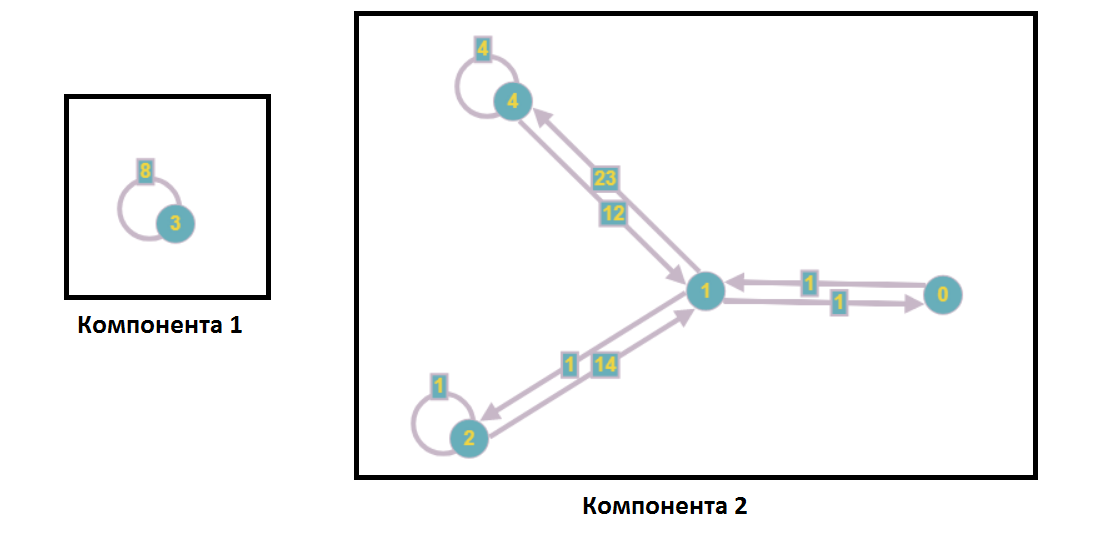
В рамках анализа системы линейных уравнений это значит, что ни одна вершина из первой компоненты не входит в уравнения с номерами второй компоненты и наоборот, то есть решать эти подсистемы мы можем независимо (например, параллельно).
Редуцирование вершин графа
Следующий шаг алгоритма — как раз то, в чём заключается оптимизация под работу с разреженными матрицами. Даже в графе из примера присутствуют “висячие” вершины, означающие, что в некоторые из уравнений входит всего одна неизвестная и, как мы знаем, значение этой неизвестной легко найти.
Чтобы определить такие уравнения, предлагается хранить массив списков, содержащих номера переменных, входящих в уравнение, имеющее номер этого элемента массива. Тогда, при достижении списком единичного размера, мы можем редуцировать ту самую “единственную” вершину, а полученное значение сообщить остальным уравнениям, в которые эта вершина входит.
Таким образом, вершину 3 из примера мы сможем редуцировать сразу, полностью обработав компоненту:
Аналогично поступим с уравнением 0, так как в него входит всего одна переменная:
Другие уравнения тоже изменятся после нахождения этого результата:
$$display$$1⋅х_1+1⋅х_2=3⇒1⋅х_2=3-1=2$$display$$
Граф принимает следующий вид:
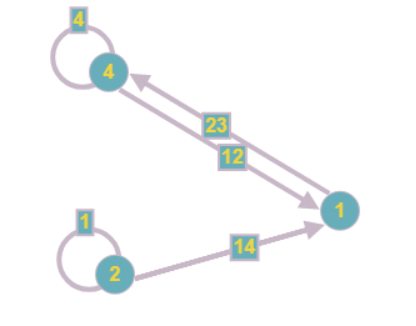
Заметим, что при редуцировании одной вершины могут возникнуть другие, тоже содержащие по одной неизвестной. Так что этот шаг алгоритма стоит повторять до тех пор, пока возможно редуцирование хотя бы одной из вершин.
Перестроение графа
Наиболее внимательные читатели могли заметить, что возможна ситуация, при которой каждая из вершин графа будет иметь степень вхождения не менее двух и продолжать последовательно редуцировать вершины будет невозможно.
Простейший пример такого графа: каждая вершина имеет степень вхождения, равную двум, ни одну из вершин нельзя редуцировать.
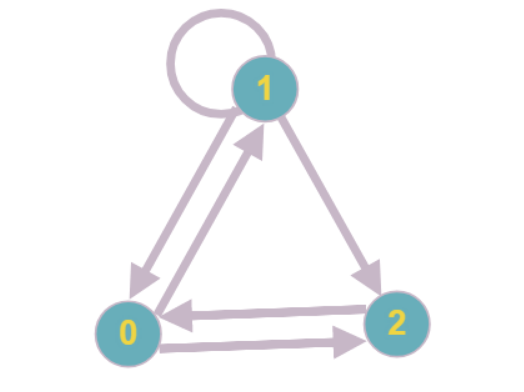
В рамках оптимизации под разреженные матрицы предполагается, что такие подграфы будут иметь малый размер, однако, работать с ними всё-таки придётся. Для расчёта значений неизвестных, входящих в подсистему уравнений, предлагается использовать классические методы решения СЛАУ (именно поэтому во введении указано, что при матрице, у которой все или почти все коэффициенты в уравнениях ненулевые, наш алгоритм будет иметь ту же асимптотическую сложность, что и стандартные).
Например, можно привести оставшееся после редуцирования множество вершин обратно в матричный вид и применить к нему метод Гаусса решения СЛАУ. Таким образом мы получим точное решение, а скорость работы алгоритма будет уменьшена за счёт обработки не всей системы, а лишь некоторой её части.
Тестирование алгоритма
Для тестирования программной реализации алгоритма мы взяли несколько реальных систем уравнений большого объёма, а также большое количество случайно сгенерированных систем.
Генерация случайной системы уравнений проходила через последовательное добавление рёбер произвольного веса между двумя случайными вершинами. Всего система заполнялась на 5-10%. Проверка корректности решений производилась через подстановку полученных ответов в исходную систему уравнений.
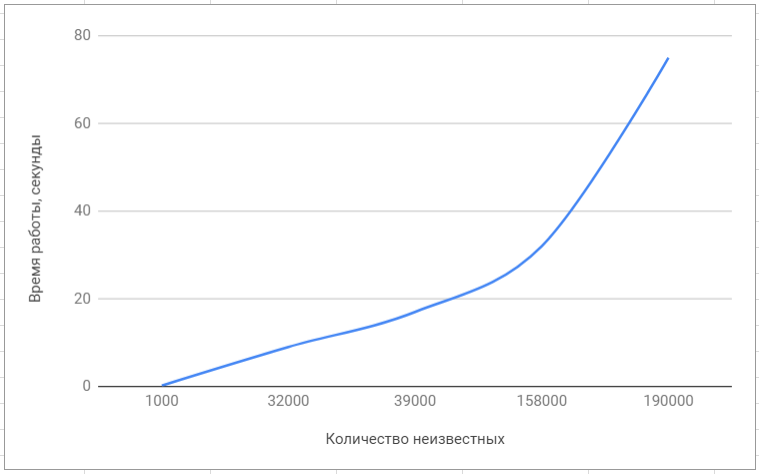
Системы имели размер от 1000 до 200000 неизвестных
Для сравнения быстродействия мы использовали наиболее популярные библиотеки для решения задач линейной алгебры, такие как superlu и lapack. Конечно, данные библиотеки ориентированы на решение широкого класса задач и решение СЛАУ в них никак не оптимизировано, поэтому различие в быстродействии оказалось значительным.
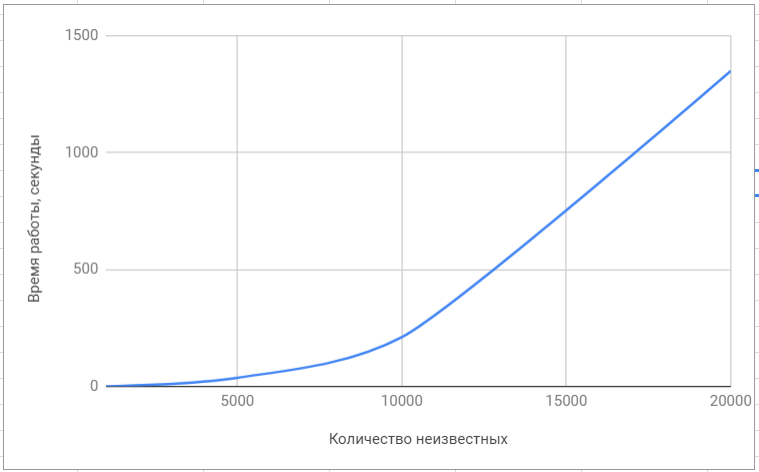
Тестирование библиотеки ‘lapack’
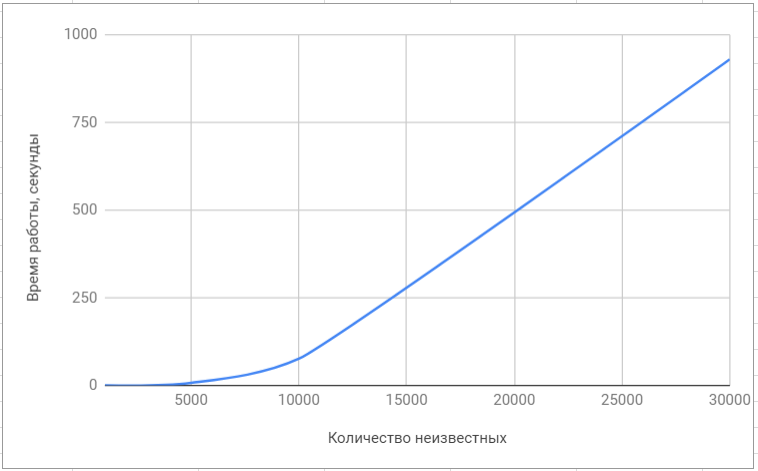
Тестирование библиотеки ‘superlu’
Приведём итоговое сравнение нашего алгоритма с алгоритмами, реализованными в популярных библиотеках:
Заключение
Даже если вы не являетесь разработчиком конфигураций «1С:Предприятие», идеи и методы оптимизации, описанные в данной статье, могут быть использованы вами не только при реализации алгоритма решения СЛАУ, но и для целого класса задач линейной алгебры, связанных с матрицами.
Для разработчиков же 1С добавим, что новая функциональность решения СЛАУ поддерживает параллельное использование вычислительных ресурсов, и можно регулировать количество используемых потоков вычисления.
Автор: PeterG








