В недавней статье «Амплитудная модуляция произвольного сигнала» её автор довольно сумбурно попытался представить своё понимание формирования спектра при амплитудной модуляции. Но отсутствие иллюстраций и избыток математики с привлечением интегральных преобразований помешало сообществу понять мысли автора и оценить статью по достоинству; в то время как тема это достаточно простая — и рассмотреть которую мы попробуем ещё раз, на этот раз с картинками и привлечением Wolfram Mathematica.
Итак, идея амплитудной модуляции состоит в том, чтобы передавать низкочастотный сигнал — голос или музыку — модулируя высокочастотный (несущий) сигнал, многократно превышающий слышимый диапазон и занимающий узкую полосу частот в радиоэфире. Сама модуляция осуществляется простым умножением сигнала на несущий:
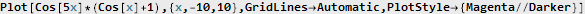
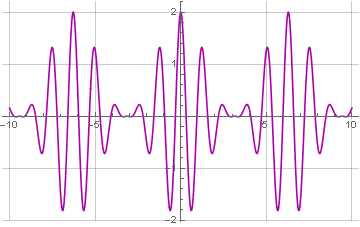
Здесь у нас в качестве несущей выступает синусоида с частотой 5:
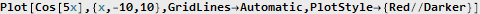
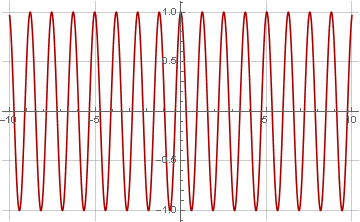
А сам сигнал — с частотой 1:
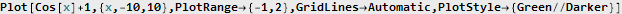
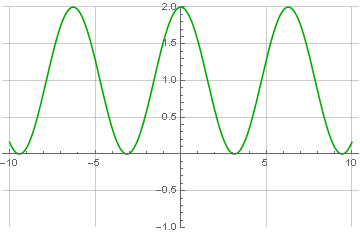
Можно заметить, что сигнал смещён вверх и имеет только положительные значения. Это не случайно и является обязательным условием для возможности последующего его корректного восстановления. Как же его восстановить? Очень просто! Нужно сдвинуть фазу промодулированного сигнала на 90 градусов (операция, известная как преобразование Гильберта), и посчитать корень из суммы квадратов модулированного и преобразованного сигналов:

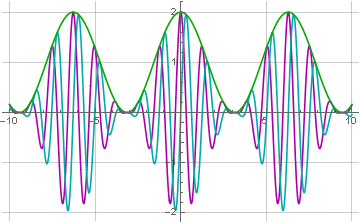
В более простом (но грубом) варианте преобразование Гильберта можно заменить задержкой сигнала на четверть периода несущий частоты, а итоговый сигнал дополнительно отфильтровать фильтром низких частот.
Теперь посмотрим, что у нас происходит со спектрами. Посчитаем преобразование Фурье от несущей:

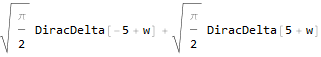
Так как дельта-функция Дирака не является функцией в классическом смысле, её график нельзя построить стандартным способом; поэтому сделаем это вручную, используя общепринятое начертание:
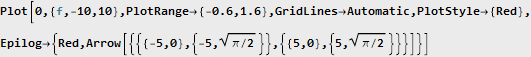
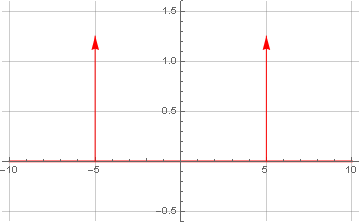
Ожидаемо получили ту же частоту, что и в начальной формуле. Наличие ещё одной такой же частоты, но со знаком минус, не случайно — это явление называется Hermitian symmetry и является следствием того, что рассматриваемая функция сугубо действительная и в комплексном представлении имеет нулевую мнимую компоненту. Отсутствие мнимых компонентов в спектре после преобразования обусловлено тем, что изначально наши функции ещё и симметричные относительно нуля, т.е. чётные.
Теперь сделаем преобразование Фурье для самого сигнала:


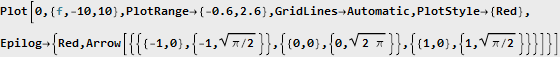
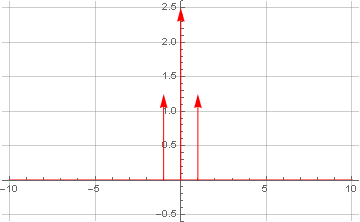
Здесь мы дополнительно получили дельта-функцию Дирака в центре координат — вследствие наличия в сигнале постоянной составляющей, которая не имеет колебаний по определению — что позволяет её рассматривать как нулевую частоту.
Что же будет со спектром, если их перемножить? Посмотрим:


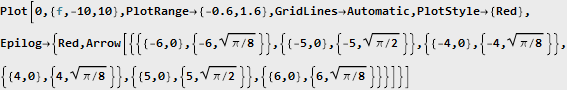
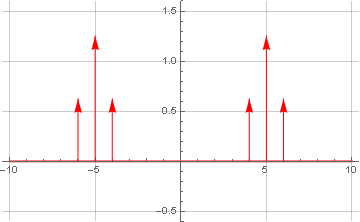
Из теории мы знаем, что умножение во временном домене равносильно свертке в частотном (и наоборот, что широко используется при FIR-фильтрации). А поскольку один из подвергаемых свёртке сигналов состоял только из одной (положительной и отрицательной) частоты, то в результате свёртки мы получили просто линейный перенос сигнала вверх по частоте (в обе стороны). И так как симметрия осталась, сигнал у нас по-прежнему не имеет мнимой компоненты.
Приведём его теперь к комплексному виду, обнулив отрицательную область частот:
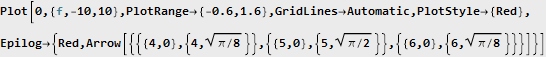
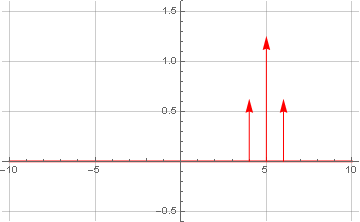
и сделав обратное преобразование Фурье:
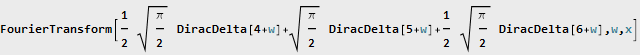
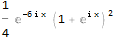
Так как функция комплексная, для построения её графика необходимо отдельно извлечь действительную и мнимую компоненты:
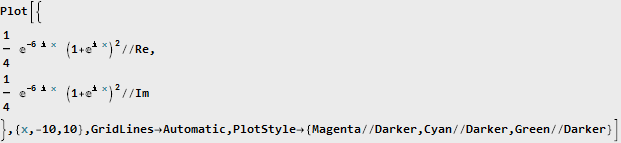
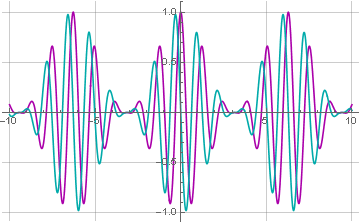
Теперь у нашего сигнала появилась мнимая компонента, представляющая собой сдвинутый на 90 градусов исходный сигнал. Это будет более очевидно, если представить полученную функцию в тригонометрическом виде:
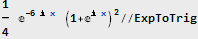
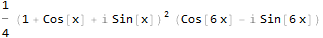
Не совсем похоже на оригинал. Попробуем упростить:
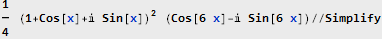
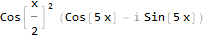
Теперь больше похоже на правду — и как видим, функция нашего исходного сигнала тоже упростилась. Попробуем её вернуть к оригинальному виду:


Множитель 1/2 появился не случайно — ведь обнулив половину спектра, мы соответственно и уменьшили мощность сигнала. Ну а теперь, имея модулированный комплексный сигнал, мы можем взять и этот модуль посчитать:

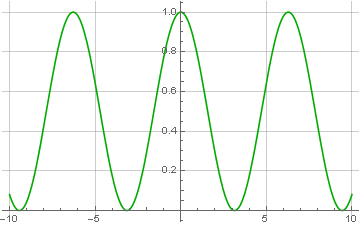
Модуль комплексного числа как раз и считается через корень суммы квадратов мнимого и действительных компонентов. И отсюда понятно, почему кодируемый сигнал должен состоять только из положительных значений — если он будет включать отрицательные значения, то после восстановления они также станут положительными, что и называется перемодуляцией:

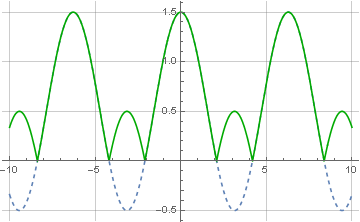
Заключение
Как видим, в рассмотрении амплитудной модуляции через преобразовании Фурье нет ничего сложного; если же рассматривать её исключительно на школьном уровне, то достаточно вспомнить, что произведение (несущей) суммы (представление сигнала в виде тригонометрического ряда) равнозначно сумме произведений (каждого члена ряда по отдельности на несущую частоту) — и, соответственно, каждое такое произведение раскладывается на сумму двух синусоид по уже озвученной автором исходной статьи формуле.
Внимательный читатель также мог заметить, что раз в результате модуляции мы получили симметричный относительно несущей частоты спектр — значит, имеет место быть избыточность данных и можно оставить только одну боковую полосу, сократив тем самым занимаемую полосу частот в радиоэфире. Такая технология действительно имеется, но это — уже совсем другая история.
Автор: Refridgerator


