Ричард Хэмминг: Глава 12. Коды с коррекцией ошибок

«Цель этого курса — подготовить вас к вашему техническому будущему.»

Привет. Помните офигенную статью «Вы и ваша работа» (+219, 2442 в закладки, 394k прочтений)?

Так вот у Хэмминга (да, да, самоконтролирующиеся и самокорректирующиеся коды Хэмминга) есть целая книга, написанная по мотивам его лекций. Мы ее переводим, ведь мужик дело говорит.

Это книга не просто про ИТ, это книга про стиль мышления невероятно крутых людей. «Это не просто заряд положительного мышления; в ней описаны условия, которые увеличивают шансы сделать великую работу.»

Мы уже перевели 26 (из 30) глав. И ведем работу над изданием «в бумаге».

Глава 12. Коды с коррекцией ошибок

(За перевод спасибо Mikhail Sheblaev, который откликнулся на мой призыв в «предыдущей главе».) Кто хочет помочь с переводом — пишите в личку или на почту magisterludi2016@yandex.ru

В этой главе затронуты две темы: первая, очевидно, коды с коррекцией ошибок, а вторая — то, как иногда происходит процесс открытия. Как Вы все знаете, я официальный первооткрыватель кодов Хэмминга с коррекцией ошибок. Таким образом я, по-видимому, имею возможность описать, как они были найдены. Но вам необходимо остерегаться любых рассказов подобного типа. По правде говоря, в то время я уже очень интересовался процессом открытия, полагая во многих случаях, что метод открытия более важен, чем то, что открыто. Я знал достаточно, чтобы не думать о процессе во время исследований, так же, как спортсмены не думают о технике, когда выступают на соревнованиях, но отрабатывают её до автоматизма. Я также выработал привычку возвращаться назад после больших или малых открытий и пытаться отследить шаги, которые к ним привели. Но не обманывайтесь; в лучшем случае я могу описать сознательную часть и малую верхушку подсознательной части, но мы просто не знаем магии работы подсознания.

Я использовал релейный вычислитель Model 5 в Нью-Йорке, подготавливая его к отправке в Aberdeen Proving Grounds вместе с некоторым требуемым программным обеспечинием (главным образом математические программы). Если с помощью 2-из-5 блочных кодов обнаруживалась ошибка, машина, оставленная без присмотра, могла до трёх раз подряд повторять ошибочный цикл, прежде чем отбросить его и взять новую задачу, надеясь, что проблемное оборудование не будет задействовано в новом решении. Я был в то время, как говорится, старшим помощником младшего дворника, свободное машинное время я получал только на выходных — с 17-00 пятницы до 8-00 понедельника — это была уйма времени! Так я мог бы загрузить входную ленту с большим количеством задач и пообещать моим друзьям, вернувшись в Мюррей Хилл, Нью-Джерси, где находился исследовательский департамент, что я подготовлю ответы ко вторнику. Ну, в одни выходные, как только мы уехали вечером пятницы, машина полностью сломалась и у меня совершенно ничего не было к понедельнику. Я должен был принести извинения моим друзьям и пообещать им ответы к следующему вторнику. Увы! Та же ситуация случилась снова! Я был мягко говоря разгневан и воскликнул: «Если машина может определить, что ошибка существует, почему же она не определит где ошибка и не исправит её, просто изменив бит на противоположный?» (На самом деле, использованные выражения были чуть крепче!).

Заметим первым делом, что этот существенный сдвиг произошёл только потому, что я испытывал огромное эмоциональное напряжение в тот момент и это характерно для большинства великих открытий. Спокойная работа позволит вам улучшить и подробнее разработать идеи, но прорыв обычно приходит только после большого стресса и эмоциональной вовлечёности. Спокойный, холодный, не вовлечённый исследователь редко делает действительно большие новые шаги.

Вернёмся к рассказу. Я знал из предыдущих обсуждений, что конечно можно было бы соорудить три экземляра вычислителя, включая сравнивающие схемы, и использовать исправление ошибок методом голосования большинства. Но чего бы это стоило! Конечно, были и лучшие методы. Я также знал, как обсуждалось в предыдущей главе, о классной штуке с контролем чётности. Я разобрался в их строении очень внимательно.
С другой стороны, Пастер сказал: «Удача любит подготовленных». Как видите, я был подготовлен моей предыдущей работой. Я более чем хорошо знал кодирование «2-из-5», я понимал их фундаментально и работал и понимал общие последствия контроля чётности.

Рис. 12.I

После некоторых размышлений я понял, что если я расположу биты любого символа сообщения в виде прямоугольника и запишу чётность каждого столбца и каждой строки, то две непрошедшие проверки чётности покажут мне координаты одной ошибки и это будет включать угловой добавленный бит чётности (который мог быть установлен соответственно, если я имел нечётные значения) Рис. 12.I. Избыточность, отношение того, что Вы используете, к минимально необходимому количеству, есть

Любому, ко изучал матанализ, очевидно, что чем ближе прямоугольник к квадрату, тем меньше избыточность для сообщения того же размера. И, конечно, большие значения m и n были бы лучше, чем малые, но тогда риск двойной ошибки был бы велик с инженерной точки зрения. Заметим, что если две ошибки случаются, то Вы имеете: (1) если они не в одной строке или столбце, то просто две строки и два столбца содержат ошибки и мы не знаем, какая диагональная пара вызвала их; (2) если две ошибки случились в одной строке (или столбце), то у вас есть только один столбец (строка) и ни одной строки (столбца).

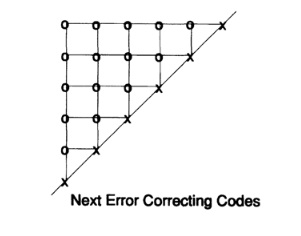
Перенесёмся сейчас на несколько недель позднее. Чтобы попасть в Нью-Йорк, я должен был добратсья чуть раньше в Мюррей Хилл, Нью-Джерси, где я работал, и прокатиться на машине, доставляющей почту для компании. Ну да, поездка через северный Нью-Джерси ранним утром не очень живописна, поэтому я завёл привычку пересматривать свои достижения, так что перо вертелось в руках автоматически. В частности я крутил в голове прямоугольные коды. Внезапно, и я не знаю причин для этого, я обнаружил, что если я возьму треугольник и размещу биты контроля чётности на диагонали с тем, чтобы каждый бит проверял столбец и строку одновременно, то я получу более приемлемую избыточность, Рис 12.II.

Моя самодовольность вмиг исчезла! Получил ли я на сей раз лучший код? Спустя несколько миль размышления по этому поводу (помните, ничего не отвлекает в пейзаже северного Нью-Джерси) я понял, что куб информационных битов с контролем чётности по каждой плоскости и проверкой чётности по осям, по всем трём осям, даст мне три координаты для ошибки ценой всего 3n-2 проверок чётности для целого кодированого сообщения длины n^3. Лучше! Но было ли это самым лучшим решением? Нет! Будучи математиком, я быстро понял, что 4-х мерный куб (я не должен был размещать биты так, только обозначить внутренние связи) будет ещё лучше. Таким образом, даже более высокая размерность была бы ещё лучше. Вскоре стало ясно (скажем, миль через 5), что куб размерности 2х2х2х… х2 с n+1 проверкой чётности был бы лучше — очевидно!

Но однажды обожегши пальцы, я не собирался соглашаться с тем, что выглядело хорошо — я уже сделал эту ошибку прежде! Мог бы я доказать, что это было лучшим решением? Как это доказать? Один очевидный подход был в том, чтобы попробовать подсчитать параметры, у меня был n+1 контрольный бит, отображаемый в строку из n+1 битов, т.е. двоичное число длины n+1 разрядов, и это могло представить произвольный объект длины 2^{n+1}. Но мне был нужен только 2^n+1 разряд, 2^n точек в кубе плюс один бит, подтверждающий, что сообщение корректно. Я не учёл в рассмотрении почти что половину битов. Увы! Я прибыл к двери компании, зарегистрировался и пошёл на конференцию, дав идее вылежаться.

Когда я возвратился к идее после нескольких дней отвлекающих событий (в конце концов, предполагалось, что я способствовал командным усилиям компании), я наконец решил, что хороший подход должен будет использовать синдром ошибки как двоичное число, указывающее место ошибки, с, конечно, всеми нулевыми битами в случае корректного результата (более лёгкий тест, чем для всех единиц на большинстве компьютеров). Заметьте, знакомство с двоичной системой, которая не была тогда распространена (1947-1948) неоднократно играло заметную роль в моих построениях. Это плата за знание большего, чем нужно сиюминутно!
Как Вы сконструируете этот частный случай кода, исправляющего ошибки? Легко! Запишите позиции в двоичном коде:

Теперь очевидно, что проверка чётности в правой половине синдрома должна включать все позиции, имеющие 1 в правом столбце; вторая цифра справа должна включить числа, имеющие 1 во втором столбце и т.д. Поэтому Вы имеете:

Таким образом, если ошибка происходит в некотором разряде, соответствующие проверки чётности (и только эти) провалятся и дадут 1 в синдроме, это составит в точности двоичное представление позиции ошибки. Это просто!

Чтобы увидеть код в действии, мы ограничимся 4 битами для сообщениями и 3 контрольными позициями. Эти числа удовлетворяют условию

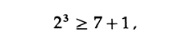
которое очевидно является необходимым условием, а равенство — достаточным. Выберем для положения битов проверки (так, чтобы контроль чётности был проще ) контрольные разряды 1, 2 и 4. Позиции для сообщения — 3, 5, 6 7. Пусть сообщение будет

1001

Мы (1) запишем сообщение в верхней строке, (2) закодируем следующую строку, (3) вставим ошибку в позиции 6 на следующей строке и (4) на следующих трёх строках вычислим три проверки чётности.

Применим проверки чётности к полученному сообщению:

Двоичное число 110 -> 6, следовательно измените в позиции 6, отбросьте контрольные разряды 1, 2 и 4 и Вы получите оригинальное сообщение, 1001.

Если это кажется волшебством, подумайте о сообщении из всех 0, которое будет иметь контрольные позиции в 0, а после представьте изменение одного бита и Вы увидите как позиция ошибки перемещается, а следом двоичное число синдрома соответственно изменится и будет точно соответствовать положению ошибки. Затем обратите внимание, что сумма любых двух корректных сообщений является всё ещё корректным сообщением (проверки чётности являются аддитивными по модулю 2, следовательно корректные сообщения образуют аддитивную группу по модулю 2). Корректное сообщение даст все нули, следовательно сумма корректных сообщений плюс ошибка одном разряде даст положение ошибки независимо от отправляемого сообщения. Проверки чётности концентрируются на ошибке и игнорируют сообщение.

Теперь сразу очевидно, что любой обмен любыми двумя или больше из столбцов, однажды согласованных на каждом конце канала, не будет иметь никакого существенного эффекта; код будет эквивалентен. Точно так же перестановка 0 и 1 в любом столбце не даст существенно различных кодов. В частности, (так называемый) Код Хемминга является просто красивым переупорядочиванием, и на практике Вы могли бы проверять контрольные биты в конце сообщения, вместо того, чтобы рассеивать их посреди сообщения.

Как насчёт двойной ошибки? Если мы хотим поймать (но не исправить) двойную ошибку, мы просто добавляем единственную новую проверку чётности к целому сообщению, которое мы отправляем. Давайте посмотрим то, что тогда произойдёт на Вашем конце канала.

Исправление одиночных ошибок плюс обнаружение двойных ошибок часто является хорошим балансом. Конечно, избыточность в коротком сообщении из 4 битов, теперь с 4 битами проверки, плоха, но число проверочных битов растёт (грубо ) как логарифм от длины сообщения. Слишком длинное сообщение — и Вы рискуете получить двойную неисправляемую ошибку (которую при помощи кода с исправлением одной ошибки Вы «исправите» в третью ошибку), слишком короткое сообщение — и стоимость избыточности слишком высока. Снова инженерные рассуждения в зависимости от конкретного случая…

Из аналитической геометрии Вы усвоили значимость использования дополняющих алгебраических и геометрических представлений. Естественное представление строки битов должно использовать n-мерный куб, каждая строка которого является вершиной куба. Используя эту картинку и наконец заметив, что любая одна ошибка в сообщении перемещает сообщение вдоль одного ребра, две ошибки — вдоль двух ребер и т.д., я медленно понял, что я должен был действовать в пространстве $L_1$. Расстояние между элементами есть количество разрядов, в которых они различаются. Таким образом у нас есть метрика на пространстве и она удовлетворяет трём стандартным условиям для расстояния (см Главу 10 где определяется стандартное расстояние в L_1).

Таким образом я должен был отнестись серьёзно к тому, что я знал как абстракцию Пифагоровой функции расстояния.

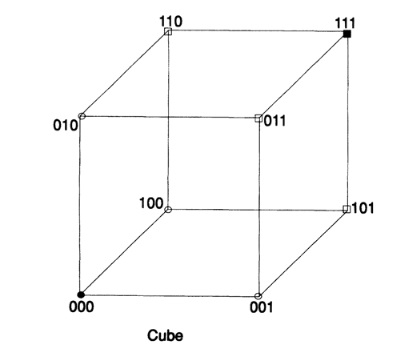
Имея понятие расстояние, мы можем определить сферу как все точки (вершины, поскольку всё рассматривается в множестве вершин), на фиксированном расстоянии от центра. Например, в 3-мерном кубе, который может быть легко нарисован, Рис. 12.III, точки (0,0,1), (0,1,0), и (1,0,0) находятся на единичном расстоянии от (0,0,0), в то время как точки (1,1,0), (1,0,1), и (0,1,1) находятся на расстоянии 2 далее, и наконец точка (1,1,1) находится на расстоянии 3 от начала координат.

Перейдём теперь в пространство с n измерениями и нарисуем сферу единичного радиуса вокруг каждой точки и предположим, что сферы не пересекаются. Очевидно, что центры сфер есть элементы кода и только эти точки, тогда результатом получения любой единичной ошибки в сообщении будет «не-кодовая» точка и Вы сможете понять откуда эта ошибка пришла. Она будет внутри сферы вокруг точки кода, которую я вам послал, что эквивалентно сфере радиуса 1 вокруг точки кода, которую Вы получили. Следовательно, у нас есть код с коррекцией ошибок. Минимальное расстояние между кодовыми точками равно 3. Если мы используем не пересекающиеся сферы радиуса 2, тогда двойная ошибка может быть исправлена, потому что полученная точка будет ближе к оригинальной кодовой точке, чем к любой другой точке; минимальное расстояние для двойной коррекции равно 5. Следующая таблица показывает эквивалентность расстояния между кодовыми точками и «исправимостью» ошибок:

Таким образом построение кода с коррекцией ошибок в точности то же, что построение множества кодовых точек в n-мерном пространстве

которое имеет необходимое минимальное расстояние между легальными сообщениями, так как условия, приведенные выше, необходимы и достаточны. Также должно быть понятно, что мы можем обменять исправление ошибок на их обнаружение — откажитесь от исправления одной ошибки и Вы получите обнаружение ещё двух вместо.

Ранее я показал как разработать коды, удовлетворяющие условиям в случае, когда минимальное расстояние равно 1,2, 3 или 4. Коды с большими минимальными расстояниями не так легко описываются и мы не пойдем далее в этом направлении. Легко найти верхнюю оценку того, насколько велики могут быть кодовые расстояния. Очевидно, что количество точек в сфере радиуса k есть (C(n, k) — биномиальный коэффициент)

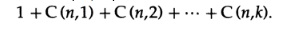
Следовательно, если мы разделим объём всего пространства, 2^n, на объём сферы, то частное будет оценкой сверху числа не пересекающихся сфер, т.е. точек кода, в соответствующем пространстве. Чтобы получить дополнительное обнаружение ошибок, мы как и прежде добавим полную проверку чётности, таким образом увеличив минимальное расстояние, которое было 2k+1, до 2k+2 (так как любые две точки на минимальном расстоянии будут иметь одинаковую чётность, увеличим минимальное расстояние на 1).

Давайте подведём итог, где мы теперь. Мы видим, что надлежащим построением кода мы можем создать систему из ненадёжных частей и получить гораздо более надёжную машину, и мы видим сколько мы должны заплатить за это оборудование, хотя мы не исследовали стоимость скорости вычисления, если мы создаём компьютер с таким уровнем коррекции ошибок. Но я ранее упомянул другую выгоду, а именно обслуживание при эксплуатации, и я хотел бы напомнить о нём снова. Чем более изощрённое оборудование, а мы очевидно движемся в этом направлении, тем более насущным является эксплуатационное обслуживание, коды с исправлением ошибок означают, что оборудование не только будет давать (возможно) верные ответы, но и может быть успешно обслужено низкоквалифицированным персоналом.

Использование кодов с обнаружением ошибок и кодов с коррекцией ошибок постоянно растёт в нашем обществе. Отправляя сообщения с космических кораблей, посланных к дальним планетам, мы часто располагаем 20 ваттами мощности или менее (возможно даже 5 ваттами) и используем коды, которые корректируют сотни ошибок в одном блоке сообщения — коррекция производится на Земле, конечно же. Когда Вы не готовы преодолеть шум как в вышеописанной ситуации или в случае «преднамеренного затора», то такие коды — единственный известный выход в этой ситуации.

В конце лета 1961 года во время профессорского отпуска я рулил через всю страну от Стэнфорда, Калифорния к Лаборатории Белл Телефоун в Нью-Джерси. Я запланировал остановку в Моррисе, Иллинойс, где телефонная компания устанавливала первую электронную телефонную станцию, которая была уже не экспериментальной. Я знал, что станция активно использовала коды Хэмминга и, конечно, я был приглашён. Мне сказали, что никогда установка не проходила так легко, как эта. Я сказал себе: «Конечно, именно это я проповедовал в течение прошлых 10 лет». Когда во время начальной наладки все модули установлены и работают должным образом (и Вы в каком-то смысле знаете, что это из-за самопроверок и корректировки), и Вы поворачиваетесь, чтобы перейти к следующим шагам, если что-то пойдёт не так, оборудование вам просто скажет об этом! Лёгкость начальной установки, а также последующего обслуживания, просто была видна невооружённым глазом! Я могу не преувеличивать, исправление ошибок не только приводило к верным результатам во время работы, но и будучи применено правильно, значительно способствовало установке и обслуживанию на месте. И чем более изощрённо оборудование, тем более важны эти вещи!

Я хочу обратиться к другой части этой главы. Я аккуратно рассказал Вам многое из того, с чем я столкнулся на каждом этапе в обнаружении кодов с коррекцией ошибок, и что я сделал. Я сделал это по двум причинам. Во-первых, я хотел быть честным с Вами и показать Вам, как легко, следуя правилу Пастера «Удача улыбнётся подготовленным», преуспеть, просто готовя себя к успеху. Да, были элементы удачи в открытии; но в почти такой же ситуации было много других людей, и они не делали этого! Почему я? Удача, что и говорить, но также я подготовил себя к пониманию того, что происходило — больше, чем другие люди вокруг, просто реагировавшие на явления, когда они происходили, и не думающие глубоко относительно того, что было скрыто под поверхностью.

Я теперь бросаю вызов Вам. То, что я записал на нескольких страницах, было сделано в течение в общей сложности приблизительно трёх — шести месяцев, главным образом рабочих, в моменты обычного исполнения моих рабочих обязанностей в компании. (Патентование отсрочило публикацию более чем на год). Может ли кто-либо сказать, что он, на моём месте, возможно, не сделал бы это? Да, Вы так же способны, как и я, были сделать это — если бы Вы были там, и Вы подготовились также!

Конечно, проживая свою жизнь, Вы не знаете к чему готовиться — Вы хотите совершить нечто значительное и не потратить всю Вашу жизнь, являясь «швейцаром науки» или чем Вы ещё занимаетесь. Конечно, удача играет видную роль. Но насколько я вижу, жизнь дарит Вам многие, многие возможности для того, чтобы сделать нечто большое (определите это как хотите сами) и подготовленный человек обычно достигает успеха один или несколько раз, а неподготовленный человек будет проваливаться почти каждый раз.

Вышеупомянутое мнение не основано на этом опыте, или просто на моих собственных событиях, это — результат изучения жизней многих великих учёных. Я хотел быть учёным, следовательно я изучил их, и я изучил открытия, произошедшие там, где я был, я задавал вопросы тем, кто сделал это. Это мнение также основано на здравом смысле. Вы растите в себе стиль выполнения больших свершений, и затем, когда возможность находится, Вы почти автоматически реагируете с максимальной крутизной в своих действиях. Вы обучили себя думать и действовать надлежащим способам.

Существует один противный тезис, который надо упомянуть, однако, что быть великим в эпоху — это не то, что нужно в последующие годы уточнить. Таким образом Вы, готовя себя к будущим великим свершениям (а их возможность более распространена и их легче достигнуть, чем Вы думаете, так как не часто распознают большие свершения, когда это происходит под носом), необходимо думать о природе будущего, в котором Вы будете жить. Прошлое является частичным руководством, и единственное, что Вы имеете помимо истории, есть постоянное использование Вашего собственного воображения. Снова, случайный перебор случайных решений не приведёт Вас куда либо так далеко, как решения, принятые с Вашим собственным видением того, каким Ваше будущее должно быть.

Я и рассказал и показал Вам, как быть великим; теперь у Вас нет оправдания того, что Вы не делаете этого!

Продолжение следует...

Кто хочет помочь с переводом, версткой и изданием книги — пишите в личку или на почту magisterludi2016@yandex.ru

Кстати, мы еще запустили перевод еще одной крутейшей книги — «The Dream Machine: История компьютерной революции»)

Автор: Алексей JetHackers Стаценко

Источник